使用 Hopfield 网络进行优化

优化是利用成本函数和能量函数的相似性，使设计、环境、资源和系统等尽可能高效的过程。霍普菲尔德网络就是一种这样的神经网络，它由一个单层组成，该层至少包含一个全连接循环神经网络。它可用于优化。

使用霍普菲尔德网络进行优化时需要记住的事情 -

• 网络中的能量函数应最小。
• 它将能够找到一个令人满意的解决方案，而不是选择其中一个存储模式。
• 霍普菲尔德网络发现的解决方案的有效性主要取决于网络中最初存在的状态。

Travelling Salesman Problem

找到推销员所走的最高效路线是计算挑战之一，可以通过使用霍普菲尔德神经网络进行改进。

TSP 的基本概念

旅行推销员问题 (TSP) 是一个经典的优化问题，推销员必须通过相互连接的多个城市，并保持成本。行驶距离最短。例如，推销员必须通过一组四个城市 A、B、C 和 D。目标是确定最有效的循环路线 A-B-C-D，以降低成本，其中包括从城市 D 到下一个城市 A 的旅行成本。

矩阵表示

n 个城市的 TSP 的每次巡回都可以用一个 n x N 矩阵来描述，其中第 i 行标识每个城市的位置。对于四个城市 A、B、C 和 D，矩阵 M 可以按以下方式表示：

霍普菲尔德网络的解决方案

当使用霍普菲尔德网络分析 TSP 的解决方案时，网络中的每个节点都连接到矩阵的特定元素。

能量函数计算

为了获得最佳结果，能量函数应尽可能低。基于上述约束，我们可以使用以下公式确定能量函数：--

约束-I

我们计算能量函数的第一个约束是，矩阵 M 的每一行中至少有一个分量为 1，并且每一行中的所有其他元素都不能大于 0，因为每个城市在 TSP 巡回中只能出现在一个位置。此约束可以数学表示如下：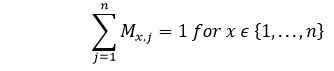

基于上述约束，现在我们将最小化能量函数，其中将包含与以下项成比例的项：

约束-II

众所周知，在 TSP 中，一个城市可以在巡回中的任何位置找到。因此，在 M 的每一列中，每个元素都必须等于 1，而其他元素必须等于 0。此限制可以数学表示如下：

基于上述约束，现在我们将最小化能量函数，其中将包含与以下项成比例的项：

成本函数计算

假设一个用 C 表示的方阵 (n x n) 是 n 个城市的 TSP 的成本矩阵，其中 n 的值大于。以下是计算成本函数时要考虑的一些参数：

• C_x,y： 成本矩阵的分量表示从一个城市到另一个城市的旅行成本。
• 以下关系演示了元素 A 和 B 之间的关系。

我们知道在矩阵中，可以确定每个节点的输出值可以是 1 或 0，因此对于每个城市对 A 和 B，我们可以为幂函数包含以下词：

基于上述成本函数，以及约束结束值的能量相关计算函数，E 可以描述如下：

这里，γ1 和 γ2 是两个权重常数。

架构

网络结构和神经元模型

霍普菲尔德网络是循环的、全连接的神经网络，其中每个神经元都接收到与所有其他神经元的连接，但不对自身连接。网络由一组二元神经元表示，这些神经元具有二元值，例如 +1 或 -1（在某些模型中为 0 和 1），以提供二元状态，网络被驱动到稳定状态。这些是能量函数最小值的状态，即优化问题的最佳解决方案。神经元根据其他神经元输入的加权和改变其状态。网络的对称性（即连接神经元 i 和 j 的权重等于连接 j 和 i 的权重）保证能量函数将随着时间的推移而减小，直到达到稳定的模式。

对称权重矩阵

霍普菲尔德网络的架构假定神经元之间的连接矩阵需要是对称的，即神经元 i 和 j 之间的链接将与 j 和 i 之间的链接相同。这种对称结构对于网络收敛到稳定状态或吸引子至关重要。权重矩阵通常根据赫布学习的概念构建，通过增加同时活跃的神经元之间的连接来保留模式。此信息被存储，然后可以用于在部分或嘈杂输入中查找完整模式，复制联想记忆的行为。

能量函数和动力学

霍普菲尔德网络的一个重要特征是其驱动网络演化的能量函数。能量是一个标量，其值随着网络更新其状态而减小，从而实现收敛。网络还异步更新，即每个神经元可以一次更新其状态，系统最终将达到能量的局部最小值。通过这种行为，可以解决组合优化问题。

收敛和联想记忆

霍普菲尔德网络最著名的特性是它们收敛到一些稳定状态，这些状态是能量景观中的局部能量最小值。当网络最初开始更新时，它会不断发展，直到达到一个稳定系统，其中所有神经元都没有进一步的转换。这些静止状态可以被视为联想记忆任务中的记录。对称权重矩阵和异步更新保证收敛。然而，当用于优化设置时，网络也可能陷入不希望的局部最小值，可能对应于错误或不完整的解决方案；这降低了它在更大、更复杂问题中的实用性。

实现和模拟

霍普菲尔德网络算法设计

建立霍普菲尔德网络的第一步是确定神经元的数量，并将它们视为问题领域中的变量或单元。最重要的阶段是参数初始化（即神经元的特定状态）、构建权重矩阵的方法（通常是赫布学习）以及根据其邻居的影响更新神经元的过程。它是一个异步学习算法：在每次迭代中，单个神经元的状态被更新（同步），从而使网络稳定。在实现时，应特别注意权重是对称的并且不应存在自连接。更新过程直到网络稳定才停止，从而象征着优化问题的可能解决方案。

编程语言和库

霍普菲尔德网络可以通过一些著名的编程语言建立，如 Python、MATLAB 和 Java。Python 特别易于使用，并且拥有广泛的科学工具生态系统，如 NumPy、TensorFlow 和 PyTorch。它们有助于使用矩阵、可视化和优化。交互式模拟和数据可视化工具，如 Jupyter Notebook，也可用且在开发和调试过程中很有价值。MATLAB 也受到学术应用的青睐，因为它提供了内置的神经网络和信号处理功能。结论是，平台的选择取决于用户和必须解决的问题领域。

模拟和观察过程

构建霍普菲尔德网络后，模拟从将初始模式输入霍普菲尔德网络开始。分布可能是存储数据点的压缩或嘈杂版本。网络随后将开始迭代更新神经元的状态。随着新更新的出现，网络状态不断演化，直到平衡，此时状态不再发生变化。在整个模拟过程中，可以跟踪网络对各种输入的反应以及解决方案的质量。在旅行推销员问题 (TSP) 等优化温度下，模拟很好地发现了网络收敛到最优或接近最优的解决方案。

与其他优化技术的比较

霍普菲尔德网络与遗传算法 (GA)

遗传算法 (GA) 和霍普菲尔德网络在解决优化问题方面相似，但在其方式上存在根本差异。GA 基于自然选择的思想，它通过交叉、变异和选择等操作，利用潜在解决方案的种群来工作。相反，霍普菲尔德网络通过最小化解决方案中的能量来分析到稳定状态。GA 非常动态，不太可能陷入局部最小值，这使其在全局优化方面非常理想。然而，GA 往往较慢，并且消耗更多的计算资源。霍普菲尔德网络可以更快地解决小问题，但如果它们没有很好地初始化或训练，它们甚至更容易陷入次优状态。

模拟退火 (SA) 与霍普菲尔德网络

模拟退火 (SA) 试图模仿金属的冷却过程来发现全局最小值。它增加了一些随机性，以逐渐降低温度，从而离开局部最小值并找到一个好的解决方案。相比之下，霍普菲尔德网络没有一种自然的方式可以超越其局部最小值，因此它们更具确定性。尽管 SA 是顺序的并且需要多次迭代，但它更适合于需要全局解决方案的复杂、非线性优化任务。

粒子群优化 (PSO) 与霍普菲尔德网络

粒子群优化 (PSO) 只是受动物社会行为启发的一种方法，它具有一群粒子（群）根据个体能力和群体围绕搜索空间移动。与霍普菲尔德网络不同，PSO 不涉及权重矩阵和能量函数。它易于应用，并且在连续搜索空间中表现良好。PSO 具有良好的全局搜索和动态环境。霍普菲尔德网络不可扩展，也不进行连续优化——然而，它们在联想记忆和二进制优化方面是有效的。

选择霍普菲尔德网络的原因

当问题可以建模为二进制优化或联想记忆问题时，霍普菲尔德网络特别有用，例如在模式识别、图像重建或解决基于约束的问题中。当用于对能量景观有很好理解的小规模场景时，它们是确定性的且延迟较低。但是，对于更复杂、更大或更动态的问题，GA、SA 或 PSO 等算法提供了更大的灵活性、可扩展性和改进的全局优化。霍普菲尔德网络在学术和理论用途中最成功，特别是当可解释性和收敛保证很重要时，但在实践中，它们在优化方面已被当代元启发式方法大大超越。

常见问题解答

哪种类型的问题（优化问题）可以用霍普菲尔德网络解决？

霍普菲尔德网络最适合解决组合优化问题。这些任务通过使用离散组合来获得解决方案，例如旅行推销员问题 (TSP)、背包问题、图着色和作业调度。优化问题通过网络映射到神经结构，稳定状态映射到最优或接近最优的解决方案。当问题可以定义为二进制选项或逻辑约束时，它可能特别有效。

霍普菲尔德网络与关系神经网络有什么区别？

霍普菲尔德网络是随机网络，并且是完全互连的，即每个神经元都连接到另一个神经元，而传统的前馈网络则不同。这种学习并非通过反向传播，而是通过能量最小化原理来描述，网络通过更新神经元值来达到稳定状态，就像霍普菲尔德网络一样。这些状态与存储的模式或解决方案相关联。另一方面，霍普菲尔德网络异步工作，单独更新。它不是为了实现深度学习或分类任务而设计的，而是更适合于联想记忆和离散优化。它们设计简单，但其数学基础使其适用于特定情况。

霍普菲尔德网络在优化方面的最大缺点是什么？

霍普菲尔德网络存在一些局限性。它们的一个主要问题是，当它们与大型或复杂问题相关联时，它们往往会陷入局部最小值。它们可能无法找到最优解，因为它们没有内置的逃逸机制，例如随机性，因为它们必须摆脱这些状态。此外，存在可伸缩性问题，其中网络的计算强度会随着神经元数量的增加而变得非常高。复杂的约束在设计权重矩阵方面存在额外的非平凡问题。这些缺点意味着霍普菲尔德网络可用于解决具有明确结构的中等规模难题，但不能解决大规模的工业优化问题。

霍普菲尔德网络是否允许实时应用？

霍普菲尔德网络往往不适用于在线优化问题，特别是那些需要快速动态适应的问题。它们遵循迭代更新和达到稳定状态的方法，这可能根据所提出问题的大小和复杂性而耗时。然而，它们可能对静态问题有效，这些问题需要快速回忆以前存储的解决方案或模式匹配。它们有时应用于混合系统，其中它们与更快的算法一起使用。然而，总的来说，它们在实时、高速环境中不实用，因为它们仅适用于离线应用或在特定应用（如图像重建）中。