自由度

在统计学中，自由度 (DF) 表示数据样本中可以自由变化的最多值，其计算方法是从总样本量中减去一。

自由度 (DF) 表示可以自由选择的次数。以两件衬衫为例，您有一次自由选择的机会。对于第二次搭配，不允许重复，所以您只能穿剩下的那件衬衫，此时自由度为零，因为最后一件衬衫是唯一的选择。在本文中，我们将探讨自由度、它的公式以及它的用途。

理解自由度？

自由度是指数据样本中独立变化的数据点最多数量。自由度是通过从总样本量中减去一来计算的，对于确保卡方检验、t 检验和 F 检验等检验的可靠性非常重要。

这些检验对于验证假设的评估很重要，自由度有助于做出决策。自由度取决于样本量。

• 当样本量小时，信息量少，导致自由度低。
• 对于较大的样本量，它提供了更多的独立见解，并且具有较高的自由度。

公式

自由度是从样本数量计算得出的。公式如下：

自由度 (DF) = N – 1

在公式中，N 表示总样本量。

不同检验公式的自由度公式

• 单样本 t 检验：DF = N-1
• 双样本 t 检验：DF = n1 + n2 – 2
• 线性回归：DF = n – 2
• 卡方拟合优度检验：DF = k – 1
• 卡方同质性检验：DF = (r – 1) (c – 1)

自由度是在卡方检验等假设检验中计算的，它允许评估是拒绝原假设还是接受原假设。

自由度示例

示例 1：选择餐食

假设您有三包食物，分别标记为 X、Y 和 Z，供一天食用。

• 早餐：早餐时，您可以选择所有三包食物。如果您选择 X 食物，还剩下两包。
• 午餐：午餐时，还剩下两包（Y 和 Z），所以您有两个选择。我们假设您选择了 Y 食物。
• 晚餐：晚餐时，只剩下一包，所以没有选择的余地了。

因此，自由度会减少；早餐的自由度是 2，午餐的自由度是 1，晚餐的自由度是 0。

示例 2：分配座位

假设有四把椅子，有四个朋友要分配座位。

• 对于第一个朋友，有 4 个可能的座位
• 对于第二个朋友，有 3 个可能的座位
• 对于第三个朋友，有 2 个可能的座位
• 对于第四个朋友，有 1 个可能的座位
• 随着座位的分配，座位的选择数量减少了。

如何确定自由度？

样本量的自由度是通过从总数据点中减去一来评估的，因为最后一个元素可以自由选择，而最后一个值是受约束的。

自由度与概率分布

自由度有助于在假设检验中定义概率分布的形状。t 检验、F 检验和卡方检验等检验依赖于自由度来评估数据的统计显著性。

在卡方检验中查找表格的自由度

卡方拟合优度

公式：，其中 是总类别数。

假设有 4 个类别，则自由度为 。

卡方独立性检验

，其中 表示行数， 表示列数。
对于一个 3x4 的表格，则

自由度与假设检验

在假设检验中，自由度 (DF) 用于评估其临界值，该临界值用于决定是拒绝原假设还是接受原假设。随着自由度的变化，t 分布和卡方分布等分布也会相应变化。

学生 t 分布

在对数据应用 t 检验时，需要学生 t 分布的临界值，该临界值由自由度 (DF) 描述。

1. 低 DF（例如 1）：分布具有非常重的尾部，非常尖峰（称为高峰分布）。
2. 中等 DF：分布变得更窄，更接近标准曲线。
3. 高 DF 几乎与标准正态分布相同，因此可以使用 z 值。

分布形状的这种变化在直观上是合理的。随着自由度的增加，t 分布的分布范围变小，因为估计的确定性增加。想象一下反复从总体中抽样并计算学生 t 值；样本量越大，检验统计量在不同样本之间变化的幅度就越小。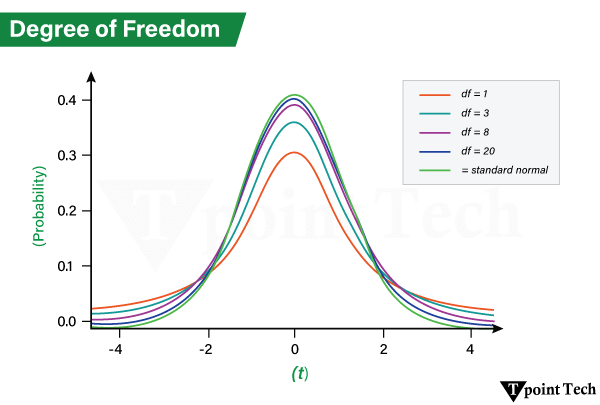

自由度的用途

自由度 (DF) 主要用于工程和数学领域，以评估完成给定问题的组合数量。在统计学中，它用于查找完成给定任务的总组合数。自由度的概念用于假设 t 检验和卡方检验。

结论

自由度表示数据集中的最大选择数。它只是在选项集中做出决策的一种方式。它用于验证 t 检验和卡方检验等统计检验的假设。