线性回归与逻辑回归

线性回归和逻辑回归是监督学习技术下的两种著名的机器学习算法。由于这两种算法本质上都是监督式的，因此它们都使用带标签的数据集进行预测。但它们之间的主要区别在于使用方式。线性回归用于解决回归问题，而逻辑回归用于解决分类问题。下面将对这两种算法进行描述，并附有区别表。

线性回归

• 线性回归是一种最简单的机器学习算法，属于监督学习技术，用于解决回归问题。
• 它用于在独立变量的帮助下预测连续的因变量。
• 线性回归的目标是找到可以准确预测连续因变量输出的最佳拟合线。
• 如果使用单个自变量进行预测，则称为简单线性回归；如果有两个以上的自变量，则称为多元线性回归。
• 通过找到最佳拟合线，算法建立了因变量和自变量之间的关系。并且关系应该是线性的。
• 线性回归的输出应仅为连续值，如价格、年龄、薪资等。因变量和自变量之间的关系如下图所示：

在上图中，因变量在Y轴（薪资）上，自变量在X轴（经验）上。回归线可以写成：

y= a0+a1x+ ε

其中，a₀和a₁是系数，ε是误差项。

逻辑回归

• 逻辑回归是最流行的机器学习算法之一，属于监督学习技术。
• 它可用于分类和回归问题，但主要用于分类问题。
• 逻辑回归用于在自变量的帮助下预测分类因变量。
• 逻辑回归问题的输出只能在0和1之间。
• 当需要两个类别之间的概率时，可以使用逻辑回归。例如，今天是否会下雨，是0还是1，真还是假等等。
• 逻辑回归基于最大似然估计的概念。根据这种估计，观测数据应具有最高概率。
• 在逻辑回归中，我们将输入的加权和通过一个激活函数，该函数可以将值映射到0到1之间。这种激活函数称为**Sigmoid函数**，得到的曲线称为Sigmoid曲线或S形曲线。请看下图：

• 逻辑回归的方程为：

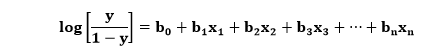线性回归与逻辑回归的区别

高级选择题：线性回归 vs. 逻辑回归

1. 您正在进行一项时间序列预测任务，股票价格是您感兴趣的变量。Fan和Tchernis（2008）的研究表明，数据存在异方差性，意味着方差不是恒定的。哪种模型对这个问题更具鲁棒性：哪种模型对这个问题更具鲁棒性？

1. 使用普通最小二乘法的线性回归
2. 使用加权最小二乘法的线性回归
3. 逻辑回归
4. 梯度提升回归

2. 一个组织希望预测客户满意度评分（介于1到5之间），这取决于他们的购买记录和客户的背景数据。考虑到所有这些因素，线性回归似乎是合理的。然而，该公司也很关心那些实际给出了5分的客户，这可以被认为是最佳满意度水平。以下哪种方法可能适用于这种情况？

1. 简单回归方法，使用了“高”满意度作为截止点
2. 有序逻辑回归。
3. 5组多项逻辑回归
4. K均值邻近回归（KDN）

3. Lasso或L1正则化以使模型稀疏而闻名。从线性回归到使用Lasso的逻辑回归，这种属性在哪些方面发生了变化？

1. 在线性回归中，一些系数有时会变为零，而在逻辑回归中，它们都会变为零。
2. 这是因为逻辑回归中采用的模型是非线性的，从而放大了稀疏性的影响。
3. 就后者而言，稀疏性在这些模型中的工作方式没有本质区别。
4. Lasso不能用于逻辑回归。

4. 您正在创建一个模型来检测欺诈。假阳性比假阴性造成的成本更高，因为真实的交易被错误地分类为欺诈。以下哪种指标最适合用于评估此任务的逻辑回归模型？

1. 精度
2. 精度
3. 召回率
4. F1分数

5. Dropout是一种常用于神经网络的优化方法。我们是否必须应用dropout来增强逻辑回归模型？为什么或为什么不？

1. 否，dropout仅用于具有多个隐藏层的神经网络。
2. 是，dropout可以用于逻辑回归模型提案的输入层。
3. 是，dropout可以在训练阶段使用，其中可以删除特定特征以防止过拟合。
4. 由于逻辑回归模型是非过拟合的，因此您不必考虑使用dropout。

6. 在逻辑回归模型中，特征的系数为正表示什么意思？

1. 随着特征值的增加，正类出现的概率也随之增加。
2. 当相关特征的值较高时，类别1的概率较低。
3. 实际上并没有直接衡量特征值与概率变化之间的关系。
4. 系数代表的值没有特定含义，但“+”或“-”有。

7. 与LASSO相比，岭回归（L2正则化）如何影响逻辑回归模型的可解释性？

1. 岭回归平均收缩所有系数，使得数据解释比Lasso更复杂。
2. 岭回归将一些系数减小到零，使其比Lasso更易于解释。
3. 岭回归和Lasso的解释性能受到同等影响。
4. 岭回归减小系数但将其设置为零，因此更容易与非正则化模型进行比较。

8. 在比较线性回归和逻辑回归模型的训练时间时，哪种说法最准确？

1. 线性回归总是训练得更快。
2. 逻辑回归总是训练得更快。
3. 训练时间取决于数据的大小和复杂性以及所选的优化算法。
4. 在大多数实际情况下，训练时间差异可以忽略不计。

9. 在两个ML模型中，哪一个更容易受到高度相关特征问题的影响？

1. 线性回归
2. 逻辑回归
3. 它们的敏感性没有区别。
4. 它们都不受特征之间相关性的影响。

10. 在哪种情况下，逻辑回归通常被认为是比SVM更好的分类任务选择？

1. 当预期存在复杂、非线性的决策边界时。
2. 当模型的可解释性和特征重要性至关重要时。
3. 当处理非常小的数据集时。
4. 当误分类的成本对于两个类别是相同时。