机器学习中的逻辑回归

2025年9月9日 | 阅读9分钟

逻辑回归是一种监督式机器学习模型，主要用于解决分类问题。与可用于预测连续值的线性回归不同，逻辑回归预测输入属于特定输入类别之一的概率。它通常用于二元任务，其中结果只有两个可能的值，例如，是/否，真/假，0/1。

该算法使用 Sigmoid 函数将输入值转换为 0-1 范围内的似然度。在本文中，我们将探讨逻辑回归的原理及其主要概念和应用。

逻辑回归的类型

根据因变量的性质，逻辑回归的类型有以下三种，按顺序排列：

二项逻辑回归

当结果变量有两个可能的类别时使用，即是/否或及格/不及格。这是最常用的，用于二元问题。

多项逻辑回归

适用于因变量属于三个或更多无序类别的情况。例如，将动物分类为猫、狗和羊。它是二元逻辑回归向多类的扩展。

有序逻辑回归

适用于因变量属于三个或更多具有特定顺序或排名的类别的情况，例如，低、中和高。在此模型中，类别的顺序被整合到预测过程中。

逻辑回归的假设

逻辑回归有一些你必须考虑的假设，因为它们是常见因素，这样你就可以确保合理的、可靠的和准确的预测。

观测的独立性

数据点也必须相互独立，即它们之间没有相关性或依赖性。

二元类型的因变量

结果变量应为二元形式，即只有两个可能的值。在处理具有两个以上类别的多维情况时，需要引入 Softmax 函数等扩展。

对数几率的线性关系

逻辑回归的假设是预测变量与因变量的对数几率之间存在线性关系。换句话说，自变量的影响与对数几率呈线性关系。

无异常值

数据不应存在强烈的异常值，因为后者会严重影响系数估计的精度。

足够大的样本量

需要相当数量的数据才能使结果一致、可靠和显著。

理解 Sigmoid 函数

Sigmoid 函数是逻辑回归的一个重要组成部分，它将原始模型输出转换为 0-1 范围内的概率值。

它将任何实值输入转换为 [0, 1] 范围内的任何数据，转换后的结果类似于 S 形曲线（等同于逻辑曲线）。由于概率应该在此范围内，因此 Sigmoid 函数适用于分类。

在逻辑回归中，将一个值（通常是 0.5）应用于 Sigmoid 输出以给出类别标签。

如果输出等于或大于阈值，则该实例被归类为类别 1。
如果输出低于阈值，则归类为类别 0。

这种机制允许将连续值转换为类别值，从而确定类别的预测。

逻辑回归方程

逻辑回归方程为：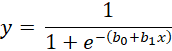

其中

x = 输入值
y = 结果的预测概率
b₀ = 截距
b₁ = 输入特征的系数

该方程假设基于输入特征的线性组合通过 Sigmoid 函数转换的二元输出的概率。

逻辑回归方程的特点

伯努利分布

逻辑回归假定结果变量是二分的，并由伯努利分布表示。结果只能取二分值（即是/否，成功/失败），逻辑回归就是为此设计的。

最大似然估计 (MLE)

与线性回归中的最小二乘法不同，逻辑回归使用最大似然估计来确定最佳拟合参数。为了能够对这些数据进行最佳估计，ELEKTRONIKA 选择系数的值来最大化给定数据的概率，目的是使模型的预测尽可能准确。

模型拟合一致性

LR 不使用 R² 作为拟合度量。它使用一致性来评估模型正确排序预测概率的程度。一致性用于查看正向结果是否与更高的预测概率正确关联。这在分类中很有用，因为目标不一定是获得最低的错误率，而是区分正确的类别。

逻辑回归的实现

逻辑回归可用于二元分类（目标变量有两个类别）和多类分类问题（目标变量有三个或更多类别）。下面使用 scikit-learn 给出这两种实现的示例。

二项逻辑回归

二项逻辑回归是一种回归分析，其中响应变量只有两个可能的值，例如 0/1 或及格/不及格。它应用 Sigmoid 函数将预测映射到概率。

我们将应用 scikit-learn 的乳腺癌数据集来生成一个逻辑回归模型分类器，该分类器将估计肿瘤是恶性还是良性。

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X, y = load_breast_cancer(return_X_y=True)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23)

clf = LogisticRegression(max_iter=10000, random_state=0)
clf.fit(X_train, y_train)

acc = accuracy_score(y_test, clf.predict(X_test)) * 100
print(f"Binomial Logistic Regression Accuracy: {acc:.2f}%")

输出

Binomial Logistic Regression Accuracy: 96.49%

多项逻辑回归

多项逻辑回归的目标变量可能假设 3 个或更多类别（无序）（例如，疾病 A、疾病 B、疾病 C）。与 Sigmoid 不同，Softmax 函数通过 Softmax 函数计算概率，以输出类别的概率。

我们将使用 scikit-learn 库中的 Digits 数据集，该数据集包含手写数字（0-9）的图像，并构建一个多项逻辑回归模型。

from sklearn.model_selection import train_test_split
from sklearn import datasets, linear_model, metrics

digits = datasets.load_digits()
X = digits.data
y = digits.target

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)

reg = linear_model.LogisticRegression(max_iter=10000, random_state=0)
reg.fit(X_train, y_train)

y_pred = reg.predict(X_test)

print(f"Multinomial Logistic Regression Accuracy: {metrics.accuracy_score(y_test, y_pred) * 100:.2f}%")

输出

Multinomial Logistic Regression Accuracy: 96.66%

逻辑回归中的术语

预测变量

用于预测目标结果的特征被称为输入特征。

因变量（目标）

可预测的、分类的变量。在二元逻辑回归中，该变量可以取 0 或 1 之类的值。

逻辑函数（Sigmoid）

用于将输入转换为 0 到 1 之间概率的数学关系，表示因变量取值为 1 的概率。

几率

事件发生概率与同一事件不发生概率的比率。与概率（限制在 0 和 1 之间）不同，几率的范围可以从 0 到无穷大。

对数几率（Logit）

几率的对数。使用逻辑回归，对数几率被建模为截距和预测变量的线性组合。

系数

模型参数，显示每个预测变量如何影响因变量。

截距

方程中的常数，表示当所有预测变量都为零时对数几率的值。

最大似然估计 (MLE)

模型系数的估计方法，通过找到增加观察特定数据集的概率的值来确定。

示例

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
from tqdm import tqdm

class LogisticRegression(nn.Module):
    def __init__(self):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(784, 10)  # 28*28 = 784

    def forward(self, x):
        x = x.view(-1, 784)  # flatten the image
        out = self.linear(x)
        return out

train_data = MNIST(root='./data', train=True, transform=ToTensor(), download=True)
test_data = MNIST(root='./data', train=False, transform=ToTensor(), download=True)

train_loader = DataLoader(train_data, batch_size=128, shuffle=True)
test_loader = DataLoader(test_data, batch_size=128, shuffle=False)

model = LogisticRegression()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

for epoch in range(10):
    running_loss = 0.0
    for images, labels in tqdm(train_loader, desc=f"Epoch {epoch+1}"):
        optimizer.zero_grad()
        outputs = model(images)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()

    print(f"Epoch {epoch+1}, Loss: {running_loss/len(train_loader):.4f}")

correct = 0
total = 0
with torch.no_grad():
    for images, labels in tqdm(test_loader, desc="Testing"):
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

accuracy = correct / total
print(f"Test Accuracy: {accuracy:.4f}")

输出

Epoch 1, Loss: 0.6762
Epoch 2, Loss: 0.4229
Epoch 3, Loss: 0.3853
Epoch 4, Loss: 0.3650
Epoch 5, Loss: 0.3541
Epoch 6, Loss: 0.3476
Epoch 7, Loss: 0.3424
Epoch 8, Loss: 0.3394
Epoch 9, Loss: 0.3363
Epoch 10, Loss: 0.3335
Testing: 100%|██████████| 79/79 [00:02<00:00, 29.89it/s]
Test Accuracy: 0.9187

逻辑回归的应用

逻辑回归已广泛应用于其他行业以解决分类问题。以下是一些重要的应用，例如：

光学字符识别 (OCR)

OCR 扫描手写或打印文本并将其转换为计算机可表示的格式。逻辑回归可用于区分图像特征，如边缘、曲线和线条，以预测特定字符的存在。这使得字符识别准确而快速。

欺诈检测

在电子商务、保险和金融领域，欺诈识别起着重要作用。在逻辑回归中，交易根据其交易金额、时间和地点被指定为合法或欺诈。这提高了识别和阻止欺诈的能力。

预测疾病传播

逻辑回归能够回归人们感染疾病的概率。它利用人口统计学、健康状况和环境因素等因素。这种预测有助于公共卫生官员更好地应对疫情。

疾病死亡率预测

医疗保健从业者利用逻辑回归来预测患者因某些疾病死亡的百分比风险。分析年龄、性别、生命体征等。这有助于做出良好的医疗决策和资源分配。

客户流失预测

企业使用逻辑回归来预测客户是否会流失。它利用客户人口统计学、行为分析和使用模式来识别可能流失的客户。这将使公司能够采取积极主动的措施来挽留他们。

逻辑回归的优点

有许多优点使逻辑回归成为解决分类问题的理想工具。

简单而有效

逻辑回归易于执行且不耗时。在数学上，它是高效的，因此在需要快速获得结果的情况下是可靠的选择。即使数据不严格符合假设，模型仍然能提供成功的性能并带来有价值的结果。

易于理解

逻辑回归的可解释性是其最大的优势之一。它不仅提供预测，还表明影响结果的变量。这尤其有用，在那些解释预测变量的作用与达到准确性同等重要性的领域。

在二元分类中有效

LGR 在两类问题中特别有用。它能快速标记未知数据，并在基本情况下非常准确。即使在多维数据集上，当准确性可能降低时，模型也能提供关于变量重要性和影响（正面或负面）的有意义信息。

逻辑回归的缺点

尽管逻辑回归非常有用，但它也有一些局限性，在复杂场景中使用时可能会降低其有效性。

仅限离散结果

逻辑回归只能预测分类结果。它无法进行连续预测，在这种情况下，线性回归或回归树等模型会更合适。

假设线性关系

该模型假定预测变量与结果的对数几率之间存在线性相关。现实世界的数据不一定是正态分布的，这需要更多的预处理或特征工程。这限制了模型反映非线性趋势的能力。

难以处理复杂数据

当预测变量不独立，或关系更为复杂时，逻辑回归可能无法完全捕捉数据的本质。在这种情况下，它可能无法捕捉重要的交互作用，只近似部分关系。

过拟合的风险

逻辑回归很容易在复杂的大型数据集上过拟合。学习噪声而不是一般模式可能会导致模型在遇到未见过的数据时性能不佳。可以通过 L1 或 L2 正则化等方法来解决，但需要仔细调整。

下一主题K-最近邻 (KNN) 算法

← 上一个下一个 →

我们提供所有技术（如 Java 教程、Android、Java 框架）的教程和面试问题

联系信息

G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India

hr@tpointtech.com

+91-9599086977

关注我们

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

机器学习

监督式学习

分类

杂项

相关教程

面试题

机器学习中的逻辑回归

逻辑回归的类型

逻辑回归的假设

理解 Sigmoid 函数

逻辑回归方程

逻辑回归方程的特点

逻辑回归的实现

二项逻辑回归

多项逻辑回归

逻辑回归中的术语

示例

逻辑回归的应用

逻辑回归的优点

逻辑回归的缺点

相关帖子

支持向量机算法

K-NN 算法

朴素贝叶斯分类器

分类算法

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器