时间序列中的平稳性检验

时间序列数据广泛应用于信号处理、气象学、金融和经济学等众多学科。它由在很长一段时间内连续收集的观测值组成。平稳性是时间序列数据分析中的一个关键概念。平稳时间序列具有稳定的统计特性，例如恒定的均值、恒定的方差以及与时间无关的自协方差。平稳性对于做出可信的预测和从数据中得出有意义的结论至关重要。

平稳过程是一个过程，其均值和方差不随时间变化，并且两个时间点之间的协方差取决于时间点之间的距离，而不是所考虑的时间点。

现在我们将实现各种平稳性检验。

代码

导入库

输出

输出

输出

用于检测的统计检验

在实践中，确定时间序列是否平稳（TSP 或 DSP）至关重要。

为此，已经开发了各种单位根和平稳性检验。其中最常用的检验是 ADF 检验、PP 检验、DF-GLS 检验、ERS 点最优检验、NP 检验和 KPSS 检验。

01. Dickey-Fuller 单位根检验

确定时间序列数据集中是否存在单位根的假设检验称为 Dickey-Fuller 检验。平均值随时间不稳以及随机趋势是序列不平稳的迹象，而单位根则意味着这些迹象。DF 检验的制定基于一个简单的自回归模型。

零假设 (H0)：时间序列具有单位根，表示不平稳。

备择假设 (H1)：时间序列是平稳的。

通过将检验统计量与从统计表中获得的临界值进行比较，来检验是否可以拒绝零假设。如果检验统计量小于临界值，则拒绝零假设并表明平稳性。相比之下，如果检验统计量大于临界值，则单位根的存在和不平稳表明零假设不能被拒绝。

输出

02. 增广 Dickey-Fuller 检验

增广 Dickey-Fuller 检验是 DF 检验的扩展，它解决了原始检验的一些潜在缺点，例如低功效和遗漏变量偏差。ADF 检验在自回归模型中加入了差分序列的附加滞后项，以处理自相关并提高检验的效率。与 DF 检验相比，ADF 检验允许更灵活的数据建模，并提供更可靠的结果，尤其是在小样本量的情况下。

输出

03. Phillip-Perron (PP) 检验

该检验以开发它的 Pierre Perron 和 Peter C. B. Phillips 的名字命名。PP 检验与 ADF 检验一样，用于确定时间序列数据集是否具有单位根或是否平稳。

PP 检验解决了一些 ADF 检验的缺点，主要是其对趋势和截距等确定性元素的定义的敏感性。由于 PP 检验是半参数和非参数的，因此它对确定性成分的存在不太敏感，并且不依赖于特定的模型规范。

具有滞后差分项的自回归模型的普通最小二乘法 (OLS) 估计是 PP 检验的检验统计量的基础。该检验的零假设是时间序列不平稳，因为它具有单位根。序列可能平稳，这是备择理论。

输出

04. 有效单位根检验

Dickey-Fuller (DF) 检验是时间序列分析和计量经济学中用于确定时间序列数据集中是否存在单位根的常用方法，而 DF-GLS 检验是 DF 检验的扩展。通过允许对底层数据生成过程进行更灵活的假设，DF-GLS 检验解决了经典 DF 检验的一些缺点。

本质上，DF-GLS 检验是一种 GLS（广义最小二乘法）回归，其误差项经过自相关和异方差调整。因此，与使用普通最小二乘法 (OLS) 估计的常规 DF 检验相比，DF-GLS 检验更可靠、更有效。

时间序列中存在单位根，表明不平稳，这是 DF-GLS 检验的零假设。序列可能平稳，这是备择理论。检验统计量在零假设下的分布是已知的，并且它是使用估计的系数及其标准误差计算的。通过将检验统计量与分布中的临界值进行比较，可以决定是否拒绝单位根的零假设。

输出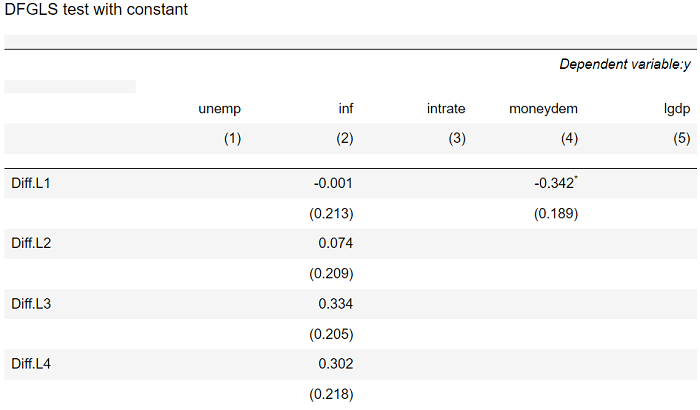

05. KPSS 检验

Kwiatkowski-Phillips-Schmidt-Shin 检验，或 KPSS 检验，是一种统计技术，用于评估时间序列数据集中的平稳零假设。与检查单位根存在的 Dickey-Fuller (DF) 和 Augmented Dickey-Fuller (ADF) 检验相比，KPSS 检验直接关注时间序列中的趋势平稳行为。

时间序列围绕确定性趋势平稳，这是 KPSS 检验的零假设。备择假设是序列具有单位根，表明不平稳。该检验将预定义分布中的临界值与观察到的序列与趋势的平方偏差之和进行比较。

检验统计量是根据该回归的平方残差之和计算的。如果检验统计量超过临界值，则拒绝零假设（平稳性）而支持不平稳性。相反，如果检验统计量小于临界值，则无法否定零假设，表明序列是平稳的。

当时间序列的方差保持恒定但时间序列的均值随时间变化时，这种现象称为趋势平稳性，KPSS 检验在识别它方面非常有用。但是，需要注意的是，KPSS 检验在识别其他类型的非平稳性（如差分平稳性或结构性断裂）方面不如其他方法有效。

输出

06. Zivot Andrews 检验

Zivot-Andrews (ZA) 检验是一种统计技术，用于确定具有结构性断裂的时间序列数据集中是否存在单位根。与假设序列平稳或遵循确定性趋势的 Dickey-Fuller (DF) 或 Augmented Dickey-Fuller (ADF) 检验等传统单位根检验不同，Zivot-Andrews 检验允许数据中存在结构性断裂或状态变化。

Zivot-Andrews 检验的零假设是时间序列不平稳，因为它具有单位根。序列可能围绕具有结构性断裂的趋势平稳，这是备择解释。因此，如果存在结构性断裂，Zivot-Andrews 检验可以识别它们发生的位置以及是否存在单位根。

Zivot-Andrews 检验统计量是根据该回归的平方残差之和计算的。如果检验统计量大于临界值，则拒绝单位根的零假设，这意味着时间序列围绕具有结构性断裂的趋势是平稳的。相反，如果检验统计量低于临界值，零假设仍然成立，表明序列中存在单位根。

当时间序列数据存在先验信息或怀疑存在结构性断裂时（例如经济政策调整、干预或其他外部因素），Zivot-Andrews 检验非常有用。

输出