Extra Trees 分类器2025年6月19日 | 阅读 10 分钟 Extra Trees 是机器学习中的另一个模型,它使用多个决策树并组合结果。与常用的随机森林策略类似,它通常能达到或超过相应的精度,并且在构建决策树集时使用的方法更简单。此外,该算法也易于使用,并且只有少数超参数以及易于使用的启发式方法来调整它们。 Extra Trees 算法简单来说,Extra Trees 是机器学习领域中一种被称为“极端随机树”(Extremely Randomized Trees)的集成方法。 它是由决策树组成的集合,与诸如自举聚合(bootstrap aggregation)和随机森林算法等其他基于树的集成技术相似。 在训练过程中,该算法会创建大量的、未剪枝的决策树。对于预测:
决策树的结果由 Extra Trees 算法分组累积,以获得一个总体输出,该输出使用多数投票来对问题进行分类,或使用算术平均来计算回归问题的值。 Extra Trees 的工作方式与 bagging 和随机森林不同。它们使用自举样本构建决策树;而 Extra Trees 则使用整个数据集来训练每棵树。随机森林使用贪婪算法来获得最佳分割点,而 Extra Trees 则在每棵树中随机决定分割点,使其更具随机性,并且树之间的相关性更低。 Extra Trees 算法以经典的自上而下的方法生成未剪枝的决策树或回归树。与其他两种算法不同之处在于:它使用完全随机的切割来分裂节点,并且不执行自举样本训练,而是使用完整样本。 三个主要的超参数控制着该算法
随机分割选择的理念是它为单个树增加了更多的随机性,而这实际上被集成中大量的树所抵消。 这些参数在将分析样本视为总体中的随机样本、过滤噪声以及接近控制模型方差的目标之间保持着权衡。 Scikit-Learn 中的 Extra Trees API如果您是第一次接触 Extra Trees 集成,从头开始训练可能会非常困难。不过,scikit-learn 为分类和回归问题都提供了非常简单的 API。 检查 Scikit-Learn 版本运行以下命令,确保您拥有最新版本的 scikit-learn: 代码 如果版本低于 0.22.1,请更新该库。 Scikit-Learn 中的 Extra TreesExtra Trees 集成在 ExtraTreesClassifier 和 ExtraTreesRegressor 类中实现,并且在功能和参数上类似。这意味着,考虑到该算法的随机性质,连续运行该算法可能会产生不同的结果。在使用此模型时,发现跨多次训练或使用重复交叉验证来评估其性能是有效的。 1. 创建数据集 代码 输出 (1000, 20) (1000,) 2. 评估模型 代码 输出 Accuracy: 0.906 (0.029) 使用 Extra Trees 进行分类Extra Trees 模型训练完成后,就可以对新数据集进行预测。使用 predict() 函数的过程包括用所有数据点拟合模型,然后进行预测。 1. 定义数据集 2. 拟合模型 代码 3. 进行预测 输出 该示例将 Extra Trees 模型应用于给定数据集,并对新输入数据行进行分类。 Predicted Class: 0 这种方法展示了该模型如何在实际场景中应用,其中数据根据分类模型中学习到的模式进行分类。然后,我们将继续演示如何将 Extra Trees API 用于回归任务。 用于回归的 Extra Trees与分类情况类似,Extra Trees 算法也可应用于回归问题。下面将展示如何使用它来解决一个合成回归问题。 步骤 1:创建回归数据集 在此上下文中,使用的 make_regression() 函数创建了一个具有 1000 个样本和 20 个预测变量的人工回归数据集。 输出 (1000, 20) (1000,) 步骤 2:评估 Extra Trees 的回归性能 在这个数据集上,我们可以采用交叉验证方法来评估 Extra Trees 算法的性能。 说明 交叉验证:重复 K-Fold 以更准确地评估系统/模型的性能。 评分:使用负平均绝对误差(neg_mean_absolute_error)来衡量准确性。 此设置评估了 Extra Trees regressor 在指定数据集上的性能和鲁棒性。之后,该算法可用于模型拟合并提供预测。 输出 Mean Absolute Error: -0.245 (0.018) 用于回归预测的 Extra TreesExtra Trees 也是执行回归任务的最终模型。其工作原理如下: 代码 输出 Prediction: 53.916 这表明了如何将训练好的模型应用于对新观测值的目标变量进行预测。 Extra Trees 超参数中的非线性树的数量作为性能的独立变量 n_estimators 参数决定了构成森林的树的数量。随着该值上升到最佳水平,性能会提高,之后性能会明显保持稳定。 代码 输出 >10 0.845 (0.043) >50 0.899 (0.025) >100 0.906 (0.026) >500 0.913 (0.024) >1000 0.911 (0.026) >5000 0.912 (0.026)  关键洞察
研究特征数量的相关性Extra Trees 算法中需要优化的一个主要超参数可以说是每次分裂随机选择的特征数量,这与随机森林类似。 如所示,该算法对该参数的确切值不太敏感,但调整该参数对于性能至关重要。 此参数通过 max_features 参数进行调整,如果留空,则等于 √V,其中 V 是输入特征的总数。例如,当固定数据集的 20 个功能属性时,建议的默认值约为 4(20 的平方根)。 下面的示例展示了实验结果,其中随机选择的特征数量从 1 更改到 20,以发现对模型准确性的影响。根据基本启发式方法,通常有一个原则是,接近 4 的较低值会产生最佳结果。 代码 输出 >1 0.895 (0.029) >2 0.903 (0.028) >3 0.903 (0.021) >4 0.907 (0.026) >5 0.905 (0.027) >6 0.909 (0.025) >7 0.908 (0.025) >8 0.912 (0.021) >9 0.909 (0.027) >10 0.908 (0.028) >11 0.911 (0.025) >12 0.910 (0.031) >13 0.908 (0.025) >14 0.913 (0.026) >15 0.908 (0.022) >16 0.910 (0.027) >17 0.907 (0.026) >18 0.907 (0.026) >19 0.906 (0.022) >20 0.908 (0.024)  关于每次分裂的最小样本数提醒读者,min_samples_split 是决策树的另一个超参数,它决定了一个节点需要多少最小样本才能进一步分裂。 此参数通过 min_samples_split 参数设置(默认值:2),它决定了决策树的深度和细节。较小的值会产生更多的分裂,这在一定程度上有助于单个树决策之间的去相关性,并可能提高集成性能。 以下示例考虑了 Extra Trees 算法在 min_samples_split 从 2 到 14 变化时的性能。 代码 输出 >2 0.912 (0.029) >3 0.905 (0.024) >4 0.908 (0.030) >5 0.904 (0.028) >6 0.906 (0.027) >7 0.902 (0.029) >8 0.897 (0.027) >9 0.898 (0.029) >10 0.896 (0.029) >11 0.891 (0.032) >12 0.889 (0.026) >13 0.888 (0.031) >14 0.891 (0.024) 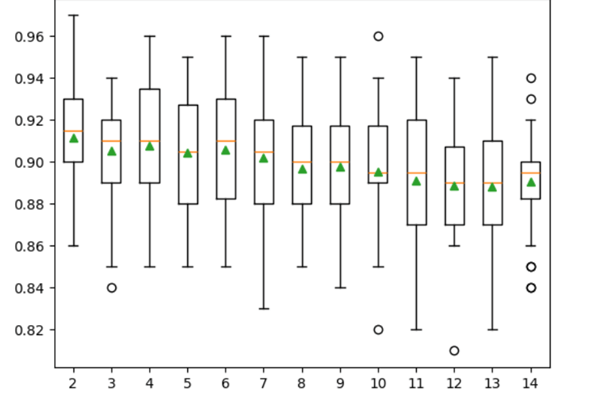 Extra Trees 分类器在特征选择方面的优势Extra Trees 分类器在特征选择方面提供了许多好处,使其成为一个强大而高效的选择。
这些优点使得 Extra Trees 分类器成为一个很好的集合工具,特别是对于高维或嘈杂的数据集,因为它非常高效且性能优异。 结论Extra Trees 算法是一种高度可靠的集成方法,在分类和回归方面都具有更高的预测能力。它通过使用随机化的决策树并使用非自举样本,引入了额外的随机性,从而提高了模型性能并降低了树之间的相关性。树的数量、随机超平面以及创建新分割所需的每个节点上的最小观测数不需要太多精细调整。其优点是它会生长未剪枝的树,并随机分割,以尽可能多的决策路径。 scikit-learn 包使得从生成数据到测试模型和进行可用预测的使用过程非常简单直接。性能估计使用交叉验证方法进行,例如重复 K-Fold。这使得 Extra Trees 特别适合实际应用,因为它能够同时处理大数据和高维度以及随机方法。由于其在学习集成方面的效率以及同时降低方差和偏差的有效性,因此应将其用于预测建模。 下一主题 |
我们请求您订阅我们的新闻通讯以获取最新更新。