机器学习中的层次聚类

层次聚类是另一种无监督机器学习算法，它用于将未标记的数据集分组到集群中，也称为层次聚类分析或HCA。

在此算法中，我们以树的形式开发集群的层次结构，这种树形结构称为树状图。

有时K均值聚类和层次聚类的结果可能看起来相似，但由于它们的工作方式不同，因此它们有所区别。因为不需要像K-均值算法那样预先确定集群的数量。

层次聚类技术有两种方法

1. 凝聚聚类（Agglomerative）： 凝聚聚类是一种自下而上的方法，其中算法从将所有数据点视为单个簇开始，然后合并它们，直到只剩下一个簇。
2. 分裂聚类（Divisive）： 分裂算法与凝聚算法相反，因为它是一种自顶向下的方法。

为什么需要层次聚类？

由于我们已经有了像K-均值聚类这样的其他聚类算法，那么为什么我们需要层次聚类呢？正如我们在K-均值聚类中所见，该算法存在一些挑战，即预先确定集群数量，并且它始终尝试创建相同大小的集群。为了解决这两个挑战，我们可以选择层次聚类算法，因为在此算法中，我们不需要预先了解集群的数量。

在本主题中，我们将讨论凝聚式层次聚类算法。

凝聚式层次聚类

凝聚式层次聚类算法是HCA的一种流行示例。为了将数据集分组到集群中，它遵循自下而上的方法。这意味着，该算法最初将每个数据集视为一个单独的簇，然后开始将最接近的簇对合并在一起。它一直这样做，直到所有簇合并成一个包含所有数据集的单个簇。

这种集群的层次结构以树状图的形式表示。

凝聚式层次聚类如何工作？

可以使用以下步骤解释AHC算法的工作原理

• 步骤1：将每个数据点创建一个单独的簇。假设有N个数据点，则簇的数量也将是N。
  
• 步骤2：选择两个最接近的数据点或簇，并将它们合并形成一个簇。因此，现在将有N-1个簇。
  
• 步骤3：再次选择两个最接近的簇，并将它们合并形成一个簇。将有N-2个簇。
  
• 步骤4：重复步骤3，直到只剩下一个簇。因此，我们将得到以下集群。考虑下面的图像
  
  
  
• 步骤5：一旦所有簇合并成一个大簇，就开发树状图，根据问题分割簇。

注意：为了更好地理解层次聚类，建议查看K-均值聚类

两个簇之间的距离度量

正如我们所见，两个簇之间的最近距离对于层次聚类至关重要。计算两个簇之间的距离有多种方法，这些方法决定了聚类的规则。这些度量称为链接方法。以下是一些流行的链接方法

1. 单链接（Single Linkage）： 这是两个簇最近点之间的最短距离。考虑下面的图像
   
2. 全链接（Complete Linkage）： 这是两个不同簇的点之间的最远距离。它是流行的链接方法之一，因为它比单链接形成更紧密的簇。
   
3. 平均链接（Average Linkage）： 这是链接方法，其中将数据集中每对数据点之间的距离相加，然后除以数据集的总数来计算两个簇之间的平均距离。它也是最流行的链接方法之一。
4. 质心链接（Centroid Linkage）： 这是链接方法，其中计算簇质心之间的距离。考虑下面的图像
   

根据上述方法，我们可以根据问题类型或业务需求应用其中任何一种。

树状图在层次聚类中的工作原理

树状图是一种类似树的结构，主要用于存储HC算法执行的每一步。在树状图图中，Y轴显示数据点之间的欧几里得距离，X轴显示给定数据集的所有数据点。

可以使用下图解释树状图的工作原理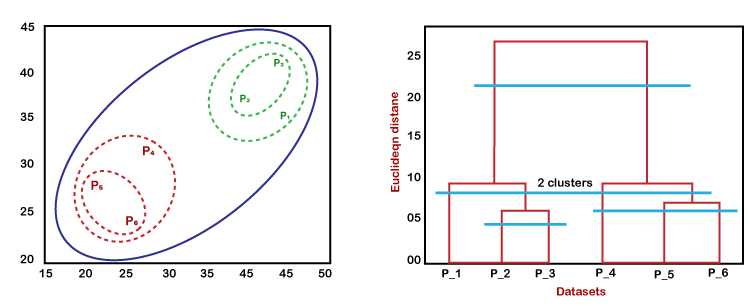

在上图中，左侧显示了凝聚聚类中集群的创建方式，右侧显示了相应的树状图。

• 如上所述，首先，数据点P2和P3组合在一起形成一个簇，相应地创建树状图，该树状图通过矩形形状连接P2和P3。高度根据数据点之间的欧几里得距离决定。
• 在下一步中，P5和P6形成一个簇，并创建相应的树状图。由于P5和P6之间的欧几里得距离略大于P2和P3，因此它比前一个更高。
• 再次，创建两个新的树状图，将P1、P2和P3组合成一个树状图，将P4、P5和P6组合成另一个树状图。
• 最后，创建最终的树状图，将所有数据点组合在一起。

我们可以根据需要，在任何级别切割树状图的树形结构。

凝聚式层次聚类的Python实现

现在，我们将使用Python来实现凝聚式层次聚类算法。为了实现这一点，我们将使用与上一个K-均值聚类主题相同的简单数据集问题，以便我们可以轻松地比较这两个概念。

该数据集包含访问商场购物的客户信息。因此，商场老板希望使用数据集信息来发现客户的一些模式或特定行为。

使用Python实现AHC的步骤

实现步骤将与K-均值聚类相同，除了某些更改，例如查找集群数量的方法。以下是步骤

1. 数据预处理
2. 使用树状图找到最佳集群数量
3. 训练层次聚类模型
4. 可视化集群

数据预处理步骤

在此步骤中，我们将为模型导入库和数据集。

• 导入库

上面的代码行用于导入执行特定任务的库，例如用于数学运算的numpy，用于绘制图形或散点图的matplotlib，以及用于导入数据集的pandas。

• 导入数据集

如上所述，我们已导入与K-均值聚类相同的Mall_Customers_data.csv数据集。考虑以下输出

• 提取特征矩阵

在这里，我们将仅提取特征矩阵，因为我们没有关于因变量的进一步信息。代码如下

这里我们只提取了3列和4列，因为我们将使用2D图来查看集群。因此，我们将年收入和支出分数作为特征矩阵。

步骤2：使用树状图找到最佳集群数量

现在，我们将为模型找到最佳集群数量。为此，我们将使用scipy库，因为它提供了一个可以直接为我们的代码返回树状图的函数。考虑以下代码行

在上面的代码行中，我们导入了scipy库的hierarchy模块。该模块为我们提供了一个方法shc.denrogram()，该方法以linkage()作为参数。链接函数用于定义两个簇之间的距离，因此我们在这里传递了x（特征矩阵）和方法“ward”，这是层次聚类中流行的链接方法。

其余的代码行用于描述树状图图的标签。

输出

通过执行上述代码行，我们将获得以下输出：

使用此树状图，我们将确定模型的最佳集群数量。为此，我们将找到最大垂直距离，该距离不会切割任何水平条。考虑下图

在上图中，我们显示了不切割水平条的垂直距离。正如我们可以可视化的那样，第4个距离看起来是最大的，所以根据这个，集群的数量将是5（该范围内的垂直线）。我们也可以取第2个数字，因为它约等于第4个距离，但我们将考虑5个集群，因为这与我们在K-均值算法中计算的相同。

因此，最佳集群数量将是5，我们将在下一步中使用它来训练模型。

步骤3：训练层次聚类模型

我们已知所需的最佳集群数量，现在可以训练我们的模型。代码如下

在上面的代码中，我们导入了scikit-learn库的cluster模块的AgglomerativeClustering类。

然后，我们创建了这个名为hc的类的对象。AgglomerativeClustering类接受以下参数

• n_clusters=5：它定义了集群的数量，我们在这里取5，因为它是最佳集群数量。
• affinity='euclidean'：它是用于计算链接的度量。
• linkage='ward'：它定义了链接标准，这里我们使用了“ward”链接。此方法是我们用于创建树状图的流行链接方法。它减少了每个簇中的方差。

在最后一行，我们创建了因变量y_pred来拟合或训练模型。它不仅训练模型，还返回每个数据点所属的簇。

执行上述代码行后，如果我们查看Sypder IDE中的变量浏览器选项，我们可以检查y_pred变量。我们可以将原始数据集与y_pred变量进行比较。考虑下图

如上图所示，y_pred显示了集群值，这意味着客户ID 1属于第5个集群（因为索引从0开始，所以4表示第5个集群），客户ID 2属于第4个集群，依此类推。

步骤4：可视化集群

现在我们可以可视化与数据集对应的集群了。

这里我们将使用与K-均值聚类相同的代码行，除了一个更改。这里我们不会绘制K-均值中绘制的质心，因为我们使用了树状图来确定最佳集群数量。代码如下

输出：通过执行上述代码行，我们将获得以下输出