EigenFaces

Eigenfaces 是计算机视觉中的一个关键概念，它提供了一种强大的面部分析和识别技术。Eigenfaces 通过利用主成分分析的数学概念，以简洁明了的方式描绘人脸照片。尽管 Eigenfaces 存在一些挑战，但它仍然持续推动面部生物识别领域的创新和研究，促进了安全、监控和人机交互等领域的发展。

Eigenfaces 由一组特征向量组成，这些特征向量是从一组人脸图像协方差矩阵中获得的。每个 Eigenface 代表了能够最好地反映数据集中面部外观最显著变化的基函数的主要成分。这些 Eigenfaces 为高维人脸图像空间提供了一个低维表示。

代码

现在我们已经使用 Olivetti 数据集完成了人脸识别，之后我们还对 Eigenfaces 进行了 PCA。目前，我们将专注于人脸识别。

导入库

Olivetti 数据集

Olivetti 数据集简介

让我们确认以上信息。

输出

输出

现在我们将展示 Olivetti 数据集中 48 位不同的个体。

输出

如上面的图库所示，数据集中包含四十位不同个体的面部照片。

现在我们将展示选定目标的 10 张人脸图像。

输出

在不同的光照、面部表情和面部细节（眼镜、胡须）的背景下，每个个体的面部都有不同的特征。

输出

分割数据集

数据集中每个个体有十张面部照片。百分之三十的面部照片将用于测试，百分之七十用于训练。为了确保每个个体拥有相同数量的训练和测试照片，使用了分层抽样（stratify）功能。每个个体将有七张训练照片和三张测试图像。测试和训练比例可以调整。

输出

输出

PCA

输出

上面的图形展示了一个虚构的二维数据集示例。在第一个图中，实际数据点以颜色区分，以便更容易辨认。程序首先寻找最大的方差方向，即“组件 1”。这是数据最相关的方向，或者说属性之间相关性最强的方向。

当算法找到一个与第一个方向正交（成直角）且包含最大信息量（方差）的方向时，它会选择该方向。在二维空间中，一个直角只有一个可能的方向；然而，在高维空间中，有多个（无限个）正交方向。

输出

输出

从下面的图形可以看出，90 个或更多的 PCA 组件对应于同一组数据。现在，让我们使用九十九个 PCA 组件来创建分类过程。

输出

我们将看一看平均脸。

输出

现在，来看 Eigenfaces。

输出

输出

模型

现在，我们将构建一个模型，该模型最终能够识别面孔。

输出

现在，我们需要训练模型。

输出

输出

我们的模型的准确率相当不错。

输出

看起来足够好了。

正如我们之前讨论过的，现在将向您展示 PCA 在实际应用中的用法。所以，我们将继续进行代码的后续部分。现在，我们将处理一个不同的数据集。

设置测试集和训练集

数据集由训练集和测试集组成。原始数据集总共有 400 张照片（40 位个体，每人 10 张照片）。下面的函数用于准备测试集，该函数保留了每位个体的一张照片作为测试集（总共 40 张），其余 360 张照片保留在训练集中。

现在，我们将可视化一些训练图像。

输出

预处理数据

在数据准备过程中，从每个特征的训练样本均值中减去均值，然后将结果除以标准差，以对图像进行中心化处理。这有两个目的：

• 数据被标准化。这样做可以避免任意大的数值。
• 它消除了所有特征的单位。这确保了单位（例如，一个以厘米为单位，另一个以米为单位）不会导致一个特征的值范围与其他特征的值范围不同。

输出

PCA

主成分分析 (PCA) 是一种统计技术，它通过正交变换，从一组可能相关的变量的观测值中创建主成分——一组线性不相关的变量值。这些主成分可以被推断为仅仅是根据其特征值排列的特征向量。代表图像的特征值最大的特征向量提供了关于该图像最多的信息。通过选择足以从图像中提取大部分显著特征的特征向量，并在该特征基上对图像向量进行正交投影，我们可以降低图像的维度。

寻找 K 的最优值

现在，我们来解决确定 K 的最优值的问题。

• 绘制特征值累积和，以确定代表训练数据中最大方差的特征向量数量。下面的图形说明了前 50 个特征占了大部分方差。
• 我们提取对应于 90% 方差的特征向量（您可以调整此数字）。<

输出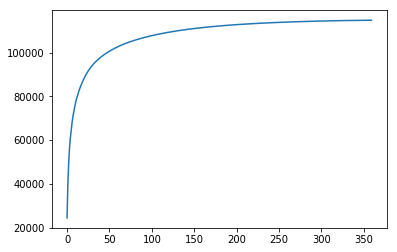

输出

输出

图像识别

PCA 是人脸识别的一个有用工具。其思想是：

• 缩小人脸图像的比例，以便能够进行识别。
• 将其与人脸类别的平均图像进行比较，在这种情况下，单个个体的平均图像对应一个类别。
• 该个体属于与平均图像的欧氏距离最短的类别，即类别由该人的面部图像表示。

输出

重构不完整图像

PCA 的另一个用途是从部分数据中重建图像。计划是将不完整图像投影到特征基的 K = 64 特征向量投影矩阵上。

输出