互补朴素贝叶斯 (CNB) 算法

朴素贝叶斯算法是众多非常流行且常用的机器学习分类算法之一。朴素贝叶斯算法有多种应用方式，例如高斯朴素贝叶斯、多项式朴素贝叶斯等。

互补朴素贝叶斯是对标准的多项式朴素贝叶斯算法的一种改进。多项式朴素贝叶斯在处理不稳定的数据时表现不佳。不平衡的数据集是指某一类实例的数量多于其他类的实例数量。这意味着样本的分布不均匀。这类数据分析起来可能很困难，因为模型很容易对这类数据过拟合，而偏向于实例更多的类别。

CNB 如何工作

互补朴素贝叶斯特别适合处理不平衡数据。在互补朴素贝叶斯中，我们不计算一个项属于特定类别的概率，而是计算一个项属于所有类别的概率。这正是该术语字面意思“互补”的含义，因此被称为互补朴素贝叶斯。

算法的逐步概述（不涉及数学）

• 计算实例不属于每个类别的可能性。
• 计算完所有类别后，我们审查所有计算出的值并选择最小值。
• 选择最小值（最低概率）是因为它不属于某个类别的概率最低。这意味着它最有可能属于该类别。这就是选择这个类别的原因。

我们来举个例子：假设有两个类别：苹果和香蕉，我们需要根据特定词频确定一个句子是与香蕉还是苹果相关。以下是基本数据集的表格表示

'苹果'类别中的总词数 = (2+1+1) + (3+4+1) + (2 + 3 + 1 + 1) = 19

'香蕉'类别中的总词数 = (1 + 1 + 3 + 9 + 6) = 20

因此，一个句子属于“苹果”类别的概率

同样，一个句子属于“香蕉”类别的概率，

在上表中，我们表示了一个数据数组。列指示了句子中使用的词语数量，并确定了句子的类别。在开始处理数据之前，我们必须先了解贝叶斯定理。

贝叶斯定理可用于计算给定另一事件发生的情况下，某个事件发生的可能性。公式为

在 A 和 B 是两个事件的情况下，P(A) 是 A 发生的可能性。P(A|B) 是在 B 事件已发生的情况下 A 发生的可能性。P(B) 意味着事件发生的可能性不能为零，因为它已经发生了。

现在我们来看看朴素贝叶斯的使用方式以及互补朴素贝叶斯如何运作。标准朴素贝叶斯算法工作原理

其中“f_i”是某个属性的频率。例如，特定单词在同一个句子中出现的次数。

对于互补朴素贝叶斯，公式是

当我们仔细检查公式时，我们会注意到互补朴素贝叶斯本质上是正常朴素贝叶斯的对立面。CNB 公式将是预测的类别。在朴素贝叶斯中，由公式得出的值最大的类别将被预测。此外，由于互补朴素贝叶斯只是 CNB 公式反过来的计算，因此由 CNB 公式计算出的值最小的类别就是预测的类别。

现在，让我们来看一个购物者示例，并尝试使用我们的 CNB 和数据对其进行建模，

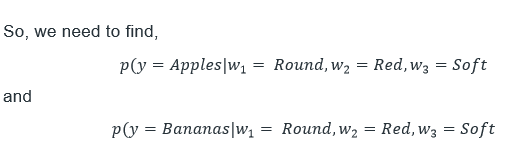有必要评估这些数字并选择具有较低值的预期类别。有必要对香蕉执行此操作并选择具有较低值的类别。即，如果 (y 等于苹果) 的值小于，则预测为苹果；但是，如果 (y = 香蕉) 的值小于 (y = 苹果) 的值，则该类别被预测为香蕉。

利用此公式，我们可以对两个类别使用互补朴素贝叶斯公式。

在当前情况下，由于 5.601 < 75.213，预测的类别将是苹果。

我们不使用值最高的类别，因为较高的值意味着包含这些单词的句子与该类别无关的可能性更高。这就是该算法被称为“互补”朴素贝叶斯的原因。

何时使用 CNB？

• 如果将要执行分类的数据集不平衡，多项式和高斯朴素贝叶斯可能会产生较低的准确率。然而，互补朴素贝叶斯将非常有效，并提供更高的准确率。
• 用于文本分类：在文本分类任务中，互补朴素贝叶斯优于高斯朴素贝叶斯和多项式朴素贝叶斯。

在 Python 中实现 CNB

在这种情况下，我们将使用葡萄酒数据集，该数据集有些偏离。它根据不同的化学参数确定葡萄酒的来源。要了解更多关于此数据集的信息，请访问此链接。

为了评估我们的模型，我们将检查测试集的准确率以及分类器的分类报告。我们将使用 scikit-learn 库来实现我们的互补朴素贝叶斯算法。

代码

输出

Accuracy of Training Set: 65.41353383458647 %

 Accuracy of Test Set: 60.0 % 


 Classifier Report : 

               precision    recall  f1-score   support

           0       0.67      0.92      0.77        13
           1       0.56      0.88      0.68        17
           2       0.00      0.00      0.00        15

    accuracy                           0.60        45
   macro avg       0.41      0.60      0.49        45
weighted avg       0.40      0.60      0.48        45

我们可以在训练集上获得 65.41% 的准确率，在测试集上获得 60.00% 的准确率。这些值相同且相当高，考虑到数据的质量。众所周知，这类数据使用我们在此案例中应用的简单分类器很难识别。因此，准确率是可以接受的。

结论

现在我们了解了互补朴素贝叶斯分类器的基本知识及其在遇到不平衡数据集时的工作原理，请尝试使用互补朴素贝叶斯进行测试。