平稳时间序列

平稳时间序列的特征是其统计属性（特别是均值、方差和自协方差）随时间保持不变。平稳性的含义是，当我们预期这些统计属性在时间上保持稳定和一致时，我们就可以预测具有相似特征（或属性）的时间序列的未来值。

更正式地说，如果我们假设时间序列只是来自同一分布的随机变量集合，那么（a）我们可以将一些关于大数定律和中心极限定理的经典统计原理应用于时间序列中的样本值，并且（b）由于我们从时间序列中采样的值是独立同分布的（IID），因此更容易估计分布的参数。

因此，大多数统计预测方法都是建立在它们类似于平稳时间序列的前提上的。然而，现实观察中的许多时间序列并非平稳。

什么是而非平稳时间序列？

非平稳时间序列的出现是由于确定性变化（如趋势或季节性行为）或随机过程单位根而导致统计特征随时间变化。当变化是确定性的时，我们可以通过去趋势或季节性调整来消除它们，而当存在单位根时，可以使用检验和差分来稳定序列。其结果是，我们可以找到一个更适合建模的时间序列的平稳版本。

分解、检验和转换非平稳信息是时间序列建模的重要活动。使序列平稳的适当转换序列不仅提高了 模型 用于预测的可用性，而且还提供了关于数据底层结构的有见地的见解。使序列平稳化使我们能够找到和开发更合适的预测模型。

理解单位根

单位根是与时间序列分析相关的重要概念，也是非平稳过程的一个主要原因。单位根指的是等于 1 的单项式项，它存在于时间序列中，产生所谓的随机趋势，或者更简单地说，是带有漂移的随机游走。这种随机趋势使得序列在预测上非常困难。数学推理可能看起来很复杂，但解释和结合单位根非常重要，因为单位根在时间序列文献中经常出现，并带来相应的模糊或不可预测的结果。增强的迪基-富勒（ADF）检验，一种标准的检验平稳性的方法，正是通过对数据进行自回归（AR）拟合模型来寻找单位根。

通常使用不同的统计检验来检查时间序列是否平稳。以下是一些统计方法的例子：

• 迪基-富勒（DF）检验： 一个简单的平稳性检验，但如果数据中存在自相关，可能会产生误导性的结果。
• 增强的迪基-富勒（ADF）检验： DF 检验的扩展，适用于更复杂的模型，通过包含滞后项来缓解自相关。仍然存在较高的假阳性率。
• 菲利普斯-普龙（PP）检验： DF 检验的修改，PP 检验对自相关和异方差（可变波动性）进行调整，通常适用于底层模型定义不明确的情况。
• Kwiatkowski-Phillips-Schmidt-Shin (KPSS) 检验： 与接受单位根或非平稳性的原假设的 ADF 或 DF 检验不同，KPSS 检验的是平稳性。虽然它可能具有较高的第一类（假阳性）错误率，但也可以与 ADF 结合使用以获得更可靠的结论。

结合这些检验通常可以提供检查时间序列是否平稳或是否需要转换（例如，差分或去趋势）以使其统计属性与平稳性保持一致的最佳机会。现在让我们看一些平稳时间序列。

代码

输出

平稳性统计检验

这里给出了两个统计检验：ADF 和 KPSS 检验。同时使用这两个检验可以更好地理解平稳性。如果一个检验未能拒绝原 假设，而另一个检验拒绝了，那么这为序列的平稳性提供了更强的证据。

1. 增强的迪基-富勒（ADF）检验

增强的迪基-富勒（ADF）检验是时间序列分析中广泛推荐的统计检验，用于检验和识别单位根的存在，单位根是非平稳过程最普遍的原因之一。ADF 检验的原假设是存在单位根，代表非平稳时间序列，而备择假设则表明是平稳或趋势平稳的 时间序列。

2. Kwiatkowski-Phillips-Schmidt-Shin (KPSS) 检验

KPSS 检验确定时间序列是否围绕均值或线性趋势平稳。而 ADF 检验则修正了围绕均值的非平稳性，KPSS 的原假设是序列是平稳的，而备择假设是序列是非平稳的。这种原假设和备择假设的对调使得 KPSS 检验与 ADF 检验在确定平稳性方面相辅相成。

如何在时间序列分析中实现平稳性？

确保平稳性是时间序列分析中的一个重要步骤，因为许多 统计模型 将基于时间序列数据底层数据的平稳性假设。如果我们现在理解了平稳性的含义以及如何检验它，我们将演示将非平稳数据转换为平稳数据的技术。

实现这种转换的两个更常见的方法包括 Box-Cox 变换和差分。当时间序列看起来具有非线性趋势（如二次或指数趋势）时，Box-Cox 变换将非常有用。在进一步分析之前，可以使用 Box-Cox 变换使数据线性化并更接近正态分布。Box-Cox 尝试找到最佳的幂变换来稳定方差并实现正态性。

代码

输出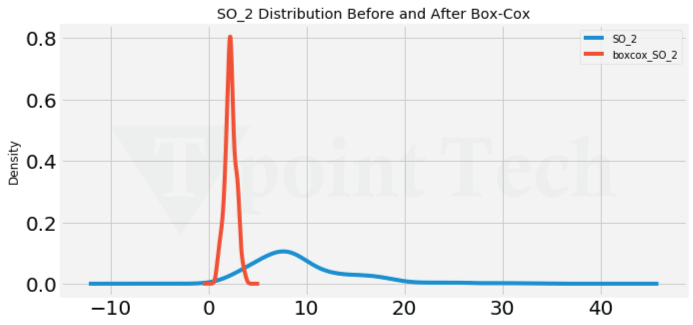

时间序列中的差分

差分是时间序列分析中的一种基本方法，用于通过消除时间序列水平的变化来稳定时间序列的均值。为了对时间序列进行差分，只需从当前观测值中减去前一个观测值，得到的序列就是连续观测值之间的差值序列。

通过对原始时间序列进行差分，我们可以将非平稳时间序列转换为平稳时间序列，该序列反映了随时间保持不变的统计属性（如均值和方差）。差分的真正技巧在于识别适当的差分阶数。最佳差分阶数通常是导致序列稳定的最低差分阶数。

一个良好差分的时间序列将围绕一个明确定义的均值波动，其自相关函数（ACF）图将迅速衰减为零。如果我们对时间序列进行过度差分（例如，应用了比必要更多的差分），时间序列可能会显得不必要地复杂；如果我们差分不足（即，使用比必要少的差分），时间序列可能不是平稳的。

代码

输出

代码

输出

自相关

相关图是时间序列分析的重要工具，它提供了关于成对观测值是否具有自相关，或者观测值的当前值是否受先前值影响的有用信息。相关图提供了一种可视化工具，用于检查观测值与先前时间点的观测值的关系，并有助于识别数据中的重复模式、趋势或常见的波动，以及季节性。

在相关图图中，x 轴表示先前时间点的滞后观测值的数量。滞后 1 是发生在前一个时间段的观测值（xt−1）。滞后 2 是第二个最后时间段的观测值，依此类推。y 轴显示当前观测值 xtobs 观测值与每个滞后观测值之间的相关强度，测量的是滞后观测值。当 y 轴的相关系数较高，并且有明显的趋势时，这表明自相关水平相对较高。

如前所述，大多数相关图表示特定置信水平的置信区间；经典相关图特征中显示的锥形通常代表 95% 的置信区间。当值落在该指定锥形或置信区间之外时，可以假设所观察到的就是真实相关性，而不仅仅是随机统计噪声。当点明显超出该锥形时，就更清楚地表明观测值确实是随机的。

偏自相关（PACF）也提供了对给定观测值与其滞后值之间关系的考察，同时控制了与中间滞后值之间的关系。PACF 主要用于消除较短滞后项的影响，以确定与滞后观测值的直接关系。

PACF 的解释方式与 ACF 类似，因为它有助于确定在 ARIMA 等时间序列模型中包含多少滞后观测值。通过分析相关图和偏自相关图作为时间序列数据的不同视图，可以深入了解时间序列的结构，并识别适合预测模型的模式和规范。

代码

输出