K-Medoids 聚类 - 理论解释

K-Medoids 和 K-Means 是分区聚类（Partition Clustering）中的两种聚类机制。首先，聚类是将一组数据点/对象划分为相似对象类的过程，使得一个簇中的所有对象都具有相似的特征。，一组 n 个对象根据它们的相似性被划分为 k 个簇。

两位统计学家 Leonard Kaufman 和 Peter J. Rousseeuw 提出了这种方法。本教程将解释 K-Medoids 的作用、其应用以及 K-Means 和 K-Medoids 之间的区别。

K-medoids 是一种无监督方法，用于对未标记数据进行聚类。它是 K-Means 算法的一种改进版本，主要设计用于处理对离群点数据敏感的问题。与其它分区算法相比，该算法简单、快速、易于实现。

划分将按照以下方式进行：

1. 每个簇必须至少包含一个对象
2. 一个对象只能属于一个簇

这里简要回顾一下 K-Means 聚类：

在 K-Means 算法中，给定 k 值和无标记数据：

1. 选择 k 个随机点（来自数据集的数据点或其他点）。这些点也称为“中心点”或“均值”。
2. 通过应用任何距离公式，如欧几里得距离、曼哈顿距离等，将数据集中的所有数据点分配给最近的中心点。
3. 现在，通过计算簇中所有数据点的均值来选择新的中心点，然后返回步骤 2。
4. 在两次迭代之间没有数据点改变分类的情况下，继续步骤 3。

K-Means 算法的问题在于算法需要处理离群点数据。离群点是一个与其他点不同的点。所有离群点数据都会出现在一个不同的簇中，并吸引其他簇与之合并。离群数据会将簇的均值提高多达 10 个单位。因此，K-Means 聚类高度受离群数据的影响。

K-Medoids

中心点（Medoid）：中心点是簇中到其他数据点的距离之和最小的点。

（或）

中心点是簇中与其他簇内点相似度（dissimilarities）最小的点。

K-Medoids 算法使用中心点（Medoid）作为参考点，而不是 K-Means 算法中的中心点（Centroid）。

K-Medoids 聚类有三种算法：

1. PAM（围绕聚类进行划分）
2. CLARA（大规模应用聚类）
3. CLARANS（随机化大规模应用聚类）

PAM 是这三种算法中最强大的，但缺点是时间复杂度高。以下 K-Medoids 使用 PAM 进行。后续部分将介绍 CLARA 和 CLARANS。

算法

给定 k 值和无标记数据

1. 从数据中选择 k 个随机点，并将这 k 个点分配给 k 个簇。这些是初始中心点（medoids）。
2. 对于所有剩余的数据点，计算它们与每个中心点的距离，并将其分配给最近中心点的簇。
3. 计算总成本（所有数据点到中心点的距离之和）
4. 选择一个随机点作为新的中心点，并将其与之前的中心点进行交换。重复步骤 2 和 3。
5. 如果新中心点的总成本低于旧中心点的成本，则使新中心点永久化，并重复步骤 4。
6. 如果新中心点的总成本高于旧中心点的成本，则撤销交换，并重复步骤 4。
7. 必须继续重复，直到出现新的中心点来分类数据点不再发生变化为止。

这里有一个例子来阐明理论：

数据集

散点图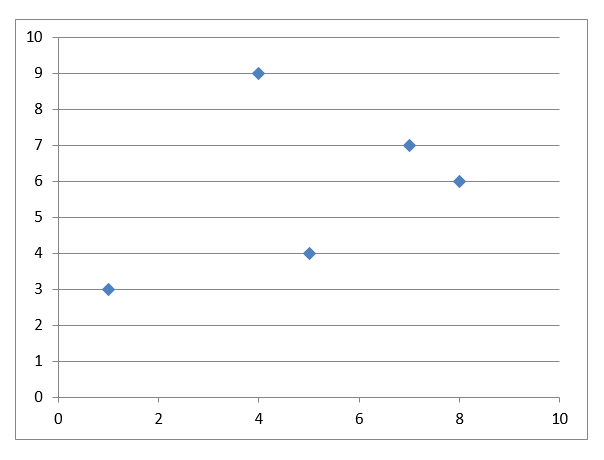

如果 k 指定为 2，我们需要将数据点划分为 2 个簇。

1. 初始中心点：M1(1, 3) 和 M2(4, 9)
2. 距离计算

曼哈顿距离：|x1 - x2| + |y1 - y2|

簇 1 0

簇 2 1, 3

1. 总成本计算
   (5) + (5 + 7) = 17
2. 随机中心点：(5, 4)

M1(5, 4) 和 M2(4, 9)

簇 1 2, 3

簇 2 1

1. 总成本计算
   (5 + 5) + 5 = 15
   低于之前的成本
   新中心点：(5, 4)。
2. 随机中心点：(7, 7)

M1(5, 4) 和 M2(7, 7)

簇 1 2

簇 2 3, 4

1. 总成本计算
   (5) + (2 + 5) = 12
   低于之前的成本
   新中心点：(7, 7)。
2. 随机中心点：(8, 6)

M1(7, 7) 和 M2(8, 6)

簇 1 4

簇 2 0, 2

1. 总成本计算
   (5) + (5 + 10) = 20
   高于之前的成本
   撤销
   因此，最终中心点：M1(5, 4) 和 M2(7, 7)
   簇 1 2
   簇 2 3, 4
   总成本：12
   簇

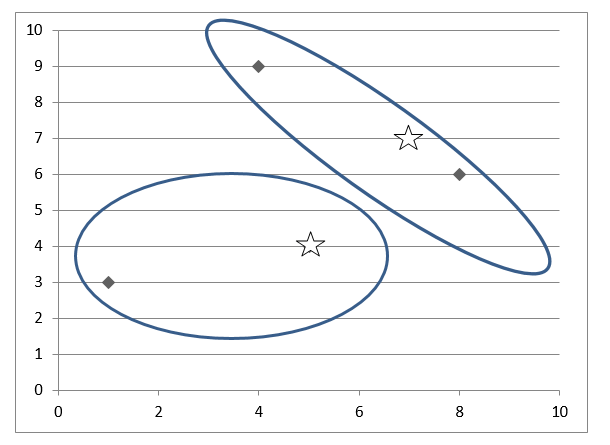PAM 的局限性

时间复杂度：O(k * (n - k)²)

每个节点的可能组合：k*(n - k)

每次计算的成本：(n - k)

总成本：k*(n - k)²

因此，PAM 适合并推荐用于小型数据集。

CLARA

它是 PAM 的扩展，用于支持大型数据集的中心点聚类。该算法从数据集中选择数据样本，对每个样本应用 Pam，并输出这些样本中最佳的聚类。这比 PAM 更有效。我们应该确保选择的样本没有偏见，因为它们会影响整个数据的聚类。

CLARANS

该算法选择一个邻居样本进行检查，而不是从数据集中选择样本。在每一步，它都会检查每个节点的邻居。该算法的时间复杂度为 O(n²)，它是所有中心点算法中最好、效率最高的。

使用 K-Medoids 的优点

1. 能有效处理噪声和离群数据
2. 易于实现且易于理解
3. 比其他分区算法更快

缺点

1. 不适合对任意形状的数据点簇进行聚类。
2. 由于初始中心点是随机选择的，因此结果可能因不同运行中的选择而异。

K-Means 与 K-Medoids

有意义的离群簇

例如，对人们收入的数据集进行聚类，以分析和理解每个簇中个人的购买和投资行为。

在这里，离群数据是高收入人群——亿万富翁。所有这样的人都倾向于购买和投资更多。因此，在这种情况下，为亿万富翁创建一个单独的簇是有意义的。

在 K-Medoids 中，它会将这些数据合并到上层阶级簇中，从而丢失了聚类中有意义的离群数据，这是 K-Medoids 在特殊情况下的一个缺点。