机器学习中的奇异值分解

SVD（奇异值分解）是一种有效的线性代数数学工具，在许多机器学习和数据科学应用中具有重要意义。它能够高效地处理大型矩阵，去除数据中的噪声，并进一步降低数据的维度。因此，SVD的应用在涉及机器学习的自然语言处理、图像压缩和推荐系统等领域得到了显著的体现。

SVD的目标是在Frobenius范数距离下，找到一类最能逼近给定矩阵的矩阵。事实上，已经证明了最佳逼近矩阵可以表示为三个不同的正交矩阵和一个对角矩阵的乘积。在这种情况下，矩阵乘法根据旋转和缩放操作转换数据点，以在转换后的空间中生成新的数据点。重要的是，对角线上的元素是原始矩阵的特征值，通过截断SVD，新空间中的信息将完全或至少部分是原始数据。SVD返回一个与原始矩阵近似但降低了秩和大小的矩阵，从而节省了计算资源，同时保留了原始矩阵的高预测精度，只要特征值沿着主对角线按降序排列。

最基本地说，SVD是一种矩阵分解算法，它将一个m x n大小的矩阵A分解为三个其他矩阵：

A = UΣVT

其中符号定义如下：

• U是一个m x m的 orthogonal（正交）矩阵，是左奇异向量的矩阵。
• Σ是一个m x n的对角矩阵，其对角线上的元素是非负的，称为奇异值。
• VT是n x n矩阵的转置，包含右奇异向量。

Σ中的每个奇异值是应用于U和V中相应奇异向量的缩放因子。矩阵A的SVD分解产生了低秩逼近；也就是说，数据被简化以实现更快的计算和减少冗余。

SVD的数学直觉

SVD基于特征值和特征向量，这是大多数人用来捕捉高维数据本质的概念。对于任何原始矩阵A，SVD通过将数据转换为由奇异值缩放的正交方向来确定数据中的模式。这些奇异值中最大的一个指示了定义数据的最重要特征，同时确保SVD选择最重要的特征，而不是噪声。

SVD在机器学习中的应用

SVD在机器学习中有多种应用方式。

• 降维：对于非常大的数据集，SVD可以通过只保留前k个奇异值及其对应的向量来降低特征的维度。这种降维，通常称为截断SVD，可以提高模型性能，因为可以在不显著损失精度的情况下降低模型的计算复杂度。
• 潜在语义分析：SVD在自然语言处理中扮演着关键角色，用于在潜在语义分析中识别词语和文档之间的关系。它捕获了大型术语-文档矩阵隐藏的语义结构，从而实现了有效的文档聚类和主题建模等任务。
• 图像压缩：SVD用于图像压缩，其中高分辨率图像通过低秩逼近来近似。由于只保留了最重要的奇异值，SVD可以有效地压缩图像，减少存储需求，同时不损失图像的整体结构。
• 推荐系统：SVD在协同过滤方面表现良好。在这里，推荐系统对用户偏好进行预测。SVD分解了用户-物品交互矩阵，捕捉了用户和物品之间的潜在关系，从而使系统能够在Netflix和Amazon等平台上做出个性化推荐。
• 降噪：SVD通过去除最小奇异值来实现数据降噪。通过较大的分量重构矩阵倾向于过滤掉细节，从而为解释提供更清晰的数据。

现在，我们将通过压缩和分析图像来演示SVD技术。

导入库

提出的SVD实现首先使用NumPy的linalg.eig函数计算矩阵乘积A^T x A的特征值和特征向量。它返回V中的右奇异向量和奇异值。最后，它按降序对奇异值及其在V中的对应奇异向量进行排序，以便最大的分量首先出现。此外，保留非零奇异值以避免复杂性。最后，通过求解涉及A、V和奇异值对角矩阵Sigma的线性方程来获得U中的左奇异向量，并获得完整、高效的SVD表示。

Σ中的奇异值在数量级上差异很大，反映了每个奇异值在数据表示中的相对重要性。为了降低维度，我们只保留前k个最大的奇异值。换句话说，我们可以截断Σ，并随后对U和V进行适当的调整。这种截断保留了原始矩阵的形状，并且不违反可行性。当SVD用于降维时，只保留U和Σ是可以的，因为V用于将降秩矩阵U Σ投影回原始维度空间。

降维

现在，我们将演示如何对scikit-learn库中提供的著名Iris数据集执行SVD分解以进行降维。

输出

这是一个自定义版本的 `sns.pairplot`，它使用小提琴图代替直方图，并绘制散点图，但根据类别标签进行着色。

输出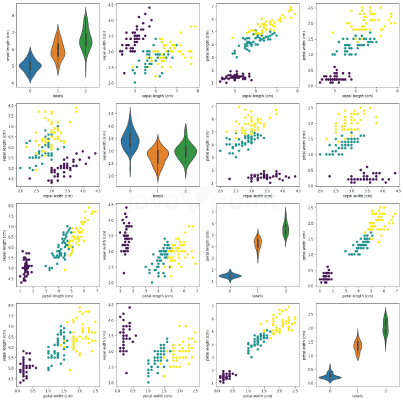

让我们应用SVD分解将数据降至两个维度（k=2）。

输出

正如我们所见，只保留两个维度仍然可以很好地分离类别。虽然在这种情况下使用所有四个特征可能没有问题，但在其他可能阻碍分析的高维数据的情况下，降维变得几乎是必不可少的。

输出

SVD图像压缩

现在，让我们看看SVD如何用于图像压缩。

除了我自己的SVD实现外，还包含了numpy.linalg SVD算法以供比较。

输出

这个动画展示了随着我们调整k值，图像如何演变。

输出

这项技术也可以通过分别对红、绿、蓝三个颜色通道应用SVD来扩展到RGB图像。

输出

生成的压缩图像可以通过存储三个截断的矩阵来表示，从而使我们能够将压缩率定义为原始未压缩大小与压缩大小的比率。此外，我们可以计算解释方差的百分比，其中每个奇异值表示它所解释的方差。一个常见的指导方针是保留足够的奇异值来解释至少85%的总方差。

输出