KL 散度

KL 散度，简称 Kullback-Leibler 散度，是衡量一个概率分布与另一个预测分布之间偏差程度的指标。它是信息理论和事实中的一个概念，广泛应用于诸如设备学习、统计学和信号处理等领域。

数学上

给定在同一域 x 上的两个概率分布 P(x) 和 Q(x)，从 Q 到 P 的 KL 散度，表示为 D_KL (P||Q)，定义为

或者，对于连续分布

KL 散度衡量使用 Q 近似 P 时丢失的信息。它不是对称的，这意味着 D_KL (P||Q)≠D_KL (Q||P)，并且它是非负的，D_KL (P||Q)≥0。当 P 和 Q 相同时，KL 散度为零，表示两个分布相同。

为了进一步理解 KL 散度，我们将尝试通过最小化 P（两个高斯分布之和）与另一个高斯分布 Q 的 KL 散度来近似分布 P。

代码

加载库

高斯分布构造

Pytorch 简化了从特定分布获取样本的过程。Torch 拥有广泛的常用分布。首先，让我们创建两个高斯分布，参数为

检查合理性

让我们在特定位置对分布进行采样，看看它是否是具有预测参数的高斯分布。

输出

上图显示分布已正确构造。

让我们将高斯分布相加并创建一个新分布 P(x)。

我们的目标将是使用另一个高斯分布 Q(x) 来近似这个新分布。我们将通过最小化分布 P(x) 和 Q(x) 之间的 KL 散度来找出参数 μQ 和 σQ。

输出

构造 Q(X)

我们将使用高斯分布来近似 P(X)。我们不确定哪些参数能最好地表示分布 P(x)。

所以，让我们从 μ=0 和 σ=1 开始。我们可能已经选择了更好的数字，因为我们已经熟悉我们试图近似的分布 (P(x))。然而，在实际环境中通常并非如此。

输出

KL 散度

Pytorch 有一个计算 KL 散度的函数。重要的是要记住，提供的输入预期具有对数概率。目标表示为概率（未应用对数）。因此，函数的第一个参数将是 Q，第二个参数将是 P（目标分布）。我们还必须谨慎处理数值稳定性。

输出

当我们求幂再取对数时，散度会变为无穷大。直接使用对数值似乎是可接受的。

输出

现在我们将定义函数 optimize_loss，它旨在优化与由均值 (mu) 和标准差 (sigma) 定义的高斯分布相关的给定损失函数 (loss_fn)。

输出

输出

让我们检查一下当我们尝试求解 P 和 Q 之间的均方距离时会发生什么。

输出

输出

我们可以观察到，结果与 KL 散度示例显著不同。当我们接近其中一个高斯曲线时，没有中间地带！

您可以尝试 μQ 的不同起始值。如果您选择接近 10（第二个高斯分布的均值）的数字，它将收敛到该值。

输出

这也可能很容易应用于 L1 损失。现在，让我们检查一下当我们尝试最大化两个分布的余弦相似度时会发生什么。

输出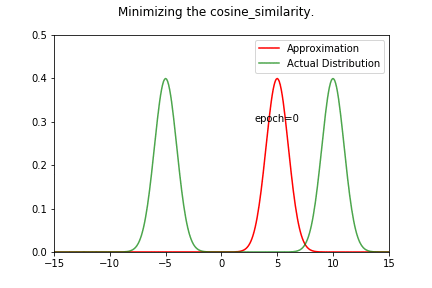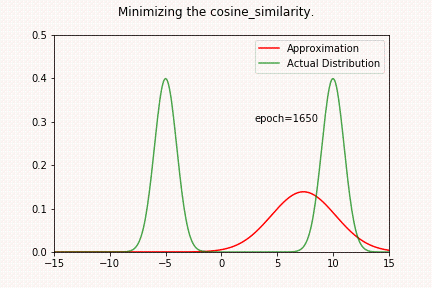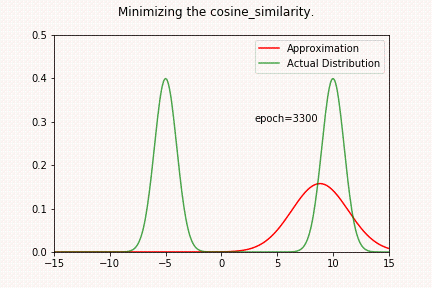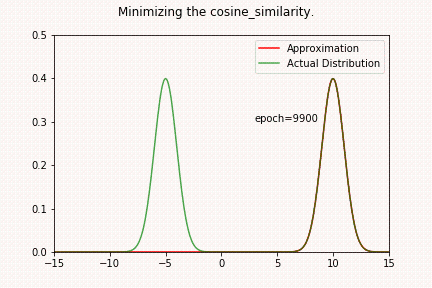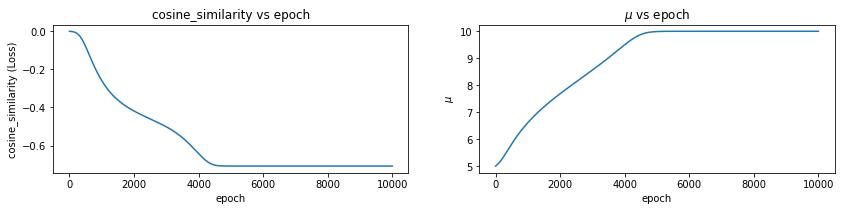

如上面的一维示例所示，我们收敛到最近的平均值。在高维环境中，存在许多谷值，最小化 MSE/L1 损失可能会有不同的结果。在深度学习中，我们随机初始化神经网络的权重。因此，同一神经网络的不同运行会收敛到不同的局部最小值是合理的。随机权重平均等技术可以通过为不同的局部最小值分配权重来提高泛化能力。不同的局部最小值可能编码有关数据集的重要信息。