栈在数据结构中的应用

在本文中，我们将了解栈在数据结构中的应用。

栈是什么意思？

栈是现代计算机中广泛使用的一种线性数据结构，其中元素的插入和删除只能在一个端点进行，即栈顶。它用于所有需要以最新插入先出的方式存储和检索数据的应用中。

栈数据结构的常见类比有桌上的一叠书、一叠盘子、乒乓球、一叠瓶盖、文本编辑器中的撤销或重做机制等。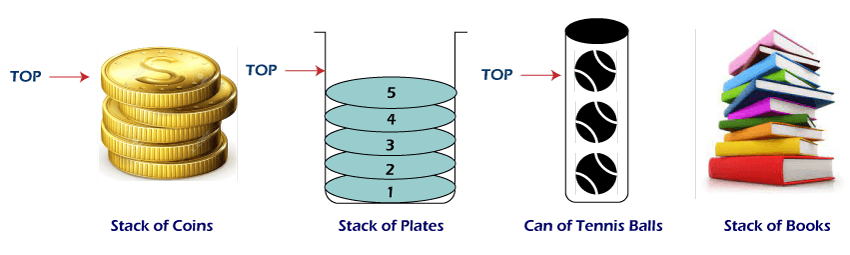

以下是栈在数据结构中的各种应用

• 算术表达式求值
• 回溯
• 分隔符检查
• 数据反转
• 函数调用处理

1. 算术表达式求值

栈是用于评估编程语言中算术表达式的非常有效数据结构。算术表达式由操作数和运算符组成。

除了操作数和运算符，算术表达式还可能包含括号，如“左括号”和“右括号”。

示例：A + (B - C)

为了评估表达式，需要了解算术表达式的标准优先级规则。五个基本算术运算符的优先级规则是

算术表达式的求值需要两个步骤

• 首先，将给定表达式转换为特殊表示法。
• 使用这种新表示法评估表达式。

算术表达式的表示法

有三种表示法来表示算术表达式

• 中缀表示法
• 前缀表示法
• 后缀表示法

中缀表示法

中缀表示法是一种方便的表达式书写方式，其中每个运算符都放在操作数之间。中缀表达式可以根据问题要求进行括号化或非括号化。

示例： A + B, (C - D) 等。

所有这些表达式都采用中缀表示法，因为运算符位于操作数之间。

前缀表示法

前缀表示法将运算符放在操作数之前。这种表示法由波兰数学家引入，因此常被称为波兰表示法。

示例： + A B, -CD 等。

所有这些表达式都采用前缀表示法，因为运算符位于操作数之前。

后缀表示法

后缀表示法将运算符放在操作数之后。这种表示法正好是波兰表示法的反向，也称为逆波兰表示法。

示例： AB +, CD+, 等。

所有这些表达式都采用后缀表示法，因为运算符位于操作数之后。

算术表达式转换为各种表示法

让我们以将中缀表达式转换为后缀表达式为例。

在上面的示例中，与后缀表达式的唯一区别是运算符放在操作数之前，而不是操作数之间。

评估后缀表达式

栈是评估后缀表达式的理想数据结构，因为栈顶元素始终是最新的操作数。栈上的下一个元素是第二个最新的待操作数。

在评估后缀表达式之前，必须检查以下条件。如果其中任何一个条件失败，则后缀表达式无效。

• 当扫描过程遇到运算符时，栈必须包含一对操作数或之前计算的中间结果。
• 当表达式完全评估后，栈必须只包含一个值。

示例

现在让我们考虑以下中缀表达式 2 * (4+3) - 5。

它的等效后缀表达式是 2 4 3 + * 5。

以下步骤说明了如何评估此后缀表达式。

2. 回溯

回溯是栈的另一个应用。它是一种递归算法，用于解决优化问题。

3. 分隔符检查

栈的常见应用是分隔符检查，即涉及语法分析源代码的解析。它也称为括号检查。当编译器将用C、C++等编程语言编写的源代码翻译成机器语言时，它通过从左到右扫描将程序解析成多个独立的部分，例如变量名、关键字等。翻译时遇到的主要问题是分隔符不匹配。我们使用不同类型的分隔符，包括括号（）、花括号{}和方括号[]，以及常见的注释分隔符/*和*/。每个开分隔符都必须与一个闭分隔符匹配，即每个开括号后面都应该有一个匹配的闭括号。此外，分隔符可以嵌套。源代码中后出现的开分隔符应该在先出现的开分隔符之前关闭。

为了执行分隔符检查，编译器会使用一个栈。当编译器翻译源代码时，它一次读取一个字符，如果找到一个开分隔符，它就将其压入栈中。当找到一个闭分隔符时，它会从栈顶弹出开分隔符并将其与闭分隔符匹配。

匹配时，可能会出现以下情况。

• 如果分隔符是相同类型的，则匹配被认为是成功的，并且过程继续进行。
• 如果分隔符不是相同类型的，则会报告语法错误。

当程序结束并且栈为空时，源代码的处理停止。

示例： 为了解释这个概念，让我们考虑以下表达式。

[{a -b) * (c -d)}/f]

4. 数据反转

要反转给定的一组数据，我们需要重新排列数据，使第一个元素和最后一个元素交换，第二个元素和倒数第二个元素交换，依此类推。

示例： 假设我们有一个字符串 Welcome，那么反转后将是 Emoclew。

有不同的反转应用

• 反转字符串
• 十进制转换为二进制

反转字符串

栈可用于反转字符串中的字符。这可以通过简单地将每个字符一个接一个地压入栈中来实现，然后可以一个接一个地从栈中弹出。由于栈的后进先出特性，字符串的第一个字符在栈底，最后一个字符在栈顶，执行弹出操作后，栈会按相反顺序返回字符串。

十进制转换为二进制

尽管十进制数在大多数商业应用中使用，但一些科学和技术应用要求使用二进制、八进制或十六进制数。栈可以用于将数字从十进制转换为二进制/八进制/十六进制形式。为了将任何十进制数转换为二进制数，我们反复将十进制数除以二，并将每次除法的余数压入栈中，直到该数变为 0。然后我们弹出整个栈，得到的结果就是给定十进制数的二进制等价物。

示例：将数字 14 从十进制转换为二进制

在上面的示例中，将 14 除以 2，我们得到商 7 和余数 0，余数被压入栈中。再次将 7 除以 2，我们得到商 3 和余数 1，余数再次被压入栈中。这个过程一直持续到给定数字减小到 0。当我们完全弹出栈时，我们得到等效的二进制数 1110。

5. 处理函数调用

栈在连续调用多个函数的程序中扮演着重要角色。假设我们有一个包含三个函数A、B和C的程序。函数A调用函数B，函数B调用函数C。

当我们调用函数A，其中包含对函数B的调用时，它的处理将不会完成，直到函数B完成执行并返回。函数B和C也类似。因此我们观察到函数A只有在函数B完成后才能完成，函数B只有在函数C完成后才能完成。因此，函数A是第一个开始的，最后一个完成的。综上所述，上述函数活动与后进先出行为匹配，并且可以使用栈轻松处理。

假设 addrA、addrB、addrC 分别是完成函数 A、B 和 C 后，控制返回的语句地址。

上图显示返回地址以函数调用顺序的相反顺序出现在栈中。每个函数完成后，执行弹出操作，并继续执行从栈中移除的地址处的代码。因此，连续调用多个函数的程序可以由栈数据结构最佳处理。控制以调用序列的相反顺序返回到每个函数的正确位置。