贪心算法与分治算法的区别

贪心算法简介

贪心算法是一种简单直观的解决优化问题的策略。它是一种算法范式，遵循在每个阶段做出局部最优选择，以期找到全局最优解的启发式方法。其思想是在不考虑当前决策对未来步骤的影响的情况下，在每一步做出可能最好的决定。

贪心算法的关键特征在于，它们通过在每一步选择最佳可用选项来做出一系列选择，而不重新审视或撤销先前的选择。这种方法通常会导致次优解，但在许多情况下，它能提供一个可接受的解决方案，并且具有计算效率高的优点。

以下是一些可以用贪心算法解决的问题的常见特征：

1. 最优子结构：问题的解决方案可以从子问题的最优解决方案构建而来。
2. 贪心选择性质：通过选择局部最优解（当前步骤中最佳可用选项）可以达到全局最优解。

虽然贪心算法相对简单高效，但它们有时可能无法保证某些问题的最佳解决方案。缺乏回溯和对未来后果的考虑可能导致次优解。因此，使用贪心算法的选择取决于具体的问题，以及贪心方法是否适用于该场景。

以下是一些经常用贪心算法解决的问题示例：

- 活动选择：给定一组具有开始和结束时间的活动，找出可以执行的最大非重叠活动数量。

- 分数背包问题：给定一组具有重量和价值的物品，确定将每件物品的一部分放入容量有限的背包中可以获得的最大价值。

- Dijkstra 最短路径算法：找出加权图中源顶点到所有其他顶点的最短路径。

- Huffman 编码：根据字符的频率构建一个最优的无前缀二进制树来对字符进行编码。

需要注意的是，虽然贪心算法在某些情况下非常强大且高效，但对于某些类型的优化问题，可能有更好的选择。在应用贪心方法之前，对问题的特征进行彻底分析和理解至关重要。

分治算法简介

分治算法是一种问题解决方法，它将一个问题分解成更小的子问题，独立地解决它们，然后将它们的解决方案组合起来以解决原始问题。“分治”一词概括了将复杂问题分解为更简单、更易于管理的组成部分的核心思想。

分治算法的典型结构涉及三个步骤：

1. 分解：将问题分解成更小的、更易于管理的子问题。此步骤递归地进行，直到子问题足够简单，可以直接解决。
2. 征服：解决子问题。这是递归的基例，此时问题足够小，可以直接解决，无需进一步细分。
3. 合并：合并子问题的解决方案，以获得原始问题的解决方案。

分治方法通常使用递归来实现，其中算法调用自身来解决子问题。每个递归调用都处理问题的一个更小的实例，直到达到基例，此时将解决方案合并以构建结果。

一些使用分治范例的经典算法示例包括：

1. 归并排序：它将数组分成两半，递归地对每一半进行排序，然后合并已排序的半部分以获得完全排序的数组。
2. 快速排序：它选择一个枢轴元素，根据枢轴将数组划分为两个子数组，递归地对每个子数组进行排序，然后合并它们。
3. 二分查找：给定一个已排序的数组，它将数组分成两半，将目标值与中间元素进行比较，并在适当的子数组中继续搜索。
4. Strassen 矩阵乘法：它将矩阵分成子矩阵，递归地计算乘积，并通过加法和减法将它们合并。

分治范例非常强大，因为它通常能产生时间复杂度高效的算法。但是，仔细设计算法以确保子问题不重叠且合并步骤高效至关重要。此外，分治算法的递归性质可能会由于函数调用堆栈而导致额外的空间需求。

总之，分治算法通过将复杂问题分解为更简单的子问题，独立解决它们，然后合并它们的解决方案，为解决复杂问题提供了一种有效的方法。

贪心算法的类型

贪心搜索的示例算法，以下是一些：

• 最小生成树 (MST) 的贪心算法
  • 问题：给定一个连通的无向图，边有权重，找出最小生成树 (MST)。
  • 算法：从任意顶点开始，贪婪地选择权重最小的边，该边将 MST 中的一个顶点连接到 MST 外的一个顶点。重复此过程，直到所有顶点都包含在 MST 中。
• 分数背包问题
  • 问题：给定一组物品，每件物品都有重量和价值，确定要放入容量有限的背包中的物品的最大价值。
  • 算法：根据价值与重量的比率贪婪地选择物品。选择价值-重量比最高的物品，直到背包装满为止。

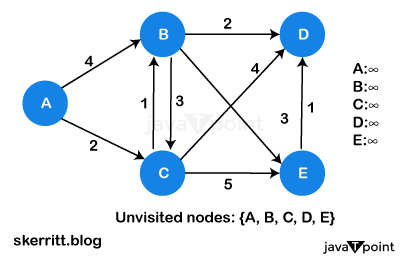
Dijkstra 最短路径算法

• 问题：给定一个带有加权边的图，找出从源顶点到所有其他顶点的最短路径。
• 算法：维护一个集合，其中包含从源的距离已知最短的顶点。在每一步，选择已知距离最小的顶点，放松其邻居的距离，并将其添加到集合中。重复此过程，直到包含所有顶点。

霍夫曼编码

• 问题：给定一组字符及其频率，找出一种二进制编码，该编码可使编码消息的总长度最小。
• 算法：通过反复组合两个频率最低的字符来构建一棵二叉树。根据树中的路径为边分配二进制代码。

活动选择问题

• 问题：给定一组具有开始和结束时间的活动，找出可以执行的最大非重叠活动数量。
• 算法：根据活动的结束时间对活动进行排序。贪婪地选择最早结束且与先前选择的活动不重叠的活动。

这些只是贪心算法的一些例子。贪心算法在每个阶段做出局部最优选择，以期找到全局最优解。需要注意的是，虽然贪心算法易于设计和实现，但它们可能并不总是保证对每个问题都能获得最优解。

实施

通过 Huffman 算法的例子来实现贪心算法。

输出

说明

提供的 Python 代码实现了用于无损数据压缩的 Huffman 编码算法。`build_huffman_tree` 函数构建了一个表示字符频率的二叉树。Huffman 码（将较短的码分配给频率较高的字符）使用 `build_huffman_codes` 函数生成。`huffman_encoding` 函数使用这些 Huffman 码对输入数据进行编码，从而产生压缩的二进制表示。编码后的数据以及 Huffman 树可用于稍后解码原始数据。该算法通过使用较短的代码表示频繁出现的字符来有效地压缩数据，从而减少了编码的总比特使用量。该实现使用优先队列和二叉树来管理 Huffman 树的构建和 Huffman 码的生成。

分治算法的应用或示例

分治是一种强大的问题解决方法，应用于各个领域。在计算机科学和算法领域，经典示例包括快速排序和归并排序算法。快速排序通过将数组划分为更小的子数组，对每个子数组进行排序并合并结果来高效地对数组进行排序。归并排序将数组分成两半；递归地对每一半进行排序，然后将它们合并以生成完全排序的数组。另一个值得注意的例子是二分查找算法，它通过重复地将已排序的数组分成两半来高效地定位特定元素。

在计算机科学之外，分治原理也应用于不同的领域。在机器人技术中，路径规划算法通常使用分治策略来导航复杂的环境。此外，在数学问题解决方法中，像快速傅立叶变换 (FFT) 这样的算法使用分治法来进行高效的信号处理。这种多功能的方法通过将复杂问题分解为更易于管理的组件来继续找到应用。

分治算法的实现。

输出

说明

提供的 Python 代码实现了二分查找算法，这是一个经典的分治策略示例。`binary_search` 函数接受一个已排序的数组 (`arr`) 和一个目标元素 (`target`) 作为参数。它分别在数组的开头和结尾初始化两个指针 (`low` 和 `high`)。然后，它迭代地计算中间索引，并将相应元素与目标进行比较。如果中间元素等于目标，则返回该索引。否则，通过根据比较结果调整指针来将搜索空间减半。此过程一直持续到找到目标或搜索空间变为空，此时返回 -1。示例用法演示了在已排序数组中搜索元素，展示了该算法在对数时间复杂度方面的效率。

分治法与贪心法的比较。

1. 分治法是一种基于解决方案的技术，而贪心法是一种优化方法。
2. 分治法可以高效地处理低复杂度问题，例如排序，而贪心法在问题复杂度增加时变得有效，例如分数背包问题和 Huffman 编码压缩。
3. 分治法通过递归来实现解决方案，而贪心法采用迭代方法来解决子问题。
4. 分治法采用自顶向下方法，即它将大问题分解为更小的子问题，然后解决它们以构建解决方案。贪心法采用自底向上方法，即它首先解决子问题，这将导致最优解决方案。
5. 分治法是递归的，因此比迭代的贪心法慢。

分治法和贪心法是两种主要的算法范式，它们具有不同的问题解决方法。

分治法的特点是将问题分解成更小、更易于管理的子问题，递归地解决它们，并将它们的解决方案合并以获得整体结果。这种范式非常适合可以自然地分解为独立子部分的问题，例如用于对数组进行排序的经典快速排序示例。它通常能产生具有对数时间复杂度的算法。

另一方面，贪心方法包括在每个阶段做出局部最优选择，并希望它们能导致全局最优解决方案。贪心算法高效且简单，但有时可能无法保证最佳解决方案。示例包括用于在图中查找最短路径的 Dijkstra 算法和用于数据压缩的 Huffman 编码。

虽然分治法强调问题分解和递归求解，但贪心法侧重于在每个步骤做出最佳选择而不重新考虑先前的决策。选择这两种方法取决于当前的问题；分治法对于更广泛的问题通常更通用，而贪心法通常因其在特定场景下的简单性和效率而受到选择。

结论

总之，分治算法和贪心算法是具有不同理念的独特问题解决方法。分治法在解决那些将问题分解为独立子问题并递归求解可获得高效解决方案（通常达到对数时间复杂度）的问题方面表现出色。相比之下，贪心算法在每个步骤做出局部最优选择，以达到全局最优解决方案。虽然贪心算法更简单、更直观，但它们可能只在某些情况下才能保证最优解决方案。在这两种范式之间进行选择取决于当前问题的性质，分治法在更广泛的场景中提供了更多的通用性，而贪心法在特定、明确定义的上下文中提供了效率。

分治法和贪心法都是被广泛使用的算法范式，它们在各种问题陈述中都有应用。我们不能说哪个比另一个更好，因为这完全取决于问题。