数据结构中的红黑树

2025 年 3 月 17 日 | 阅读 31 分钟

红黑树是一种二叉搜索树。学习红黑树的前提是我们应该了解二叉搜索树。在二叉搜索树中，左子树中节点的值应小于根节点的值，右子树中节点的值应大于根节点的值。

红黑树中的每个节点都包含一个额外的位，用于表示颜色，以确保在对树进行的任何操作（如插入、删除等）期间树都是平衡的。在二叉搜索树中，平均情况下搜索、插入和删除需要O(log2n)时间，最好情况下为O(1)，最坏情况下为O(n)。

让我们来理解二叉搜索树的不同情况。

在上图的树中，如果我们想搜索 80。我们将首先将 80 与根节点进行比较。80 大于根节点，即 10，因此搜索将在右子树中进行。再次，80 与 15 进行比较；80 大于 15，因此我们移到 15 的右侧，即 20。现在，我们到达叶节点 20，而 20 不等于 80。因此，它会显示元素在树中未找到。每次操作后，搜索都会减半。上述 BST 将花费 O(logn) 时间来搜索元素。

上图显示了右倾斜的 BST。如果我们想在树中搜索 80，我们将与所有节点进行比较，直到找到元素或到达叶节点。因此，上述右倾斜的 BST 将花费O(N)时间来搜索元素。

在上述 BST 中，第一个是平衡的 BST，而第二个是不平衡的 BST。从上述两个二叉搜索树中，我们可以得出结论，对于对树执行的任何操作，平衡树所需的时间少于不平衡树。

因此，我们需要一棵平衡树，而红黑树是一种自平衡二叉搜索树。现在，问题出现了，为什么我们需要红黑树，如果 AVL 也是一棵高度平衡树。红黑树用于因为当树很大时，AVL 树需要大量的旋转，而红黑树最多需要两次旋转来平衡树。AVL 树和红黑树之间的主要区别在于 AVL 树是严格平衡的，而红黑树不是完全高度平衡的。因此，AVL 树比红黑树更平衡，但红黑树保证所有操作（如插入、删除和搜索）的 O(log2n) 时间。

在 AVL 树中插入更容易，因为 AVL 树是严格平衡的，而红黑树中删除和搜索更容易，因为红黑树需要的旋转次数更少。

顾名思义，节点要么是红色或黑色。有时不需要旋转，只需要重新着色即可平衡树。

红黑树的性质

它是一种自平衡二叉搜索树。这里的自平衡意味着它通过旋转或重新着色节点来自己平衡树。
这种树数据结构之所以命名为红黑树，是因为每个节点都是红色或黑色的。每个节点都存储一个额外的称为位的标识符，该标识符表示节点的颜色。例如，0 位表示黑色，1 位表示红色。节点存储的其他信息与二叉树类似，即数据部分、左指针和右指针。
在红黑树中，根节点始终是黑色的。
在二叉树中，我们将没有子节点的节点视为叶节点。相比之下，在红黑树中，没有子节点的节点被视为内部节点，这些节点连接到始终为黑色的 NIL 节点。NIL 节点是红黑树中的叶节点。
如果节点是红色的，则其子节点应为黑色。换句话说，我们可以说不应该有红-红父子关系。
从节点到其任何后代 NIL 节点的每条路径都应具有相同数量的黑色节点。

每棵 AVL 树都可以是红黑树吗？

是的，每棵 AVL 树都可以是红黑树，如果我们给每个节点着色为红色或黑色。但并非每棵红黑树都是 AVL 树，因为 AVL 树是严格高度平衡的，而红黑树并非完全高度平衡。

红黑树中的插入

以下是一些用于创建红黑树的规则：

如果树为空，则将新节点创建为黑色根节点。
如果树非空，则将新节点创建为红色叶节点。
如果新节点的父节点为黑色，则退出。
如果新节点的父节点为红色，则必须检查新节点父节点的同级节点的颜色。

4a) 如果颜色为黑色，则执行旋转和重新着色。

4b) 如果颜色为红色，则重新着色节点。我们还需要检查新节点的父节点的父节点是否为根节点；如果不是根节点，我们将重新着色并重新检查节点。

让我们来理解红黑树中的插入。

10, 18, 7, 15, 16, 30, 25, 40, 60

步骤 1：最初，树是空的，所以我们创建了一个值为 10 的新节点。这是树的第一个节点，所以它将是树的根节点。正如我们已经讨论过的，根节点必须是黑色的，如下所示：

步骤 2：下一个节点是 18。由于 18 大于 10，它将放在 10 的右侧，如下所示：

我们知道红黑树的第二个规则，即如果树非空，则新创建的节点将为红色。因此，节点 18 为红色，如下所示：

现在我们验证红黑树的第三个规则，即新节点的父节点是否为黑色。在上图中，父节点为黑色；因此，它是一棵红黑树。

步骤 3：现在，我们创建了值为 7 的新节点，颜色为红色。由于 7 小于 10，它将放在 10 的左侧，如下所示：

现在我们验证红黑树的第三个规则，即新节点的父节点是否为黑色。正如我们可以观察到的，节点 7 的父节点是黑色的，并且它遵守红黑树的属性。

步骤 4：下一个元素是 15，15 大于 10 但小于 18，所以新节点将在节点 18 的左侧创建。由于树非空，节点 15 将为红色。

上图违反了红黑树的属性，因为它存在红-红父子关系。现在我们必须应用一些规则来创建一棵红黑树。规则 4 说：如果新节点的父节点是红色的，那么我们必须检查新节点父节点的同级节点的颜色。新节点是节点 15；新节点的父节点是节点 18，父节点的同级节点是节点 7。由于父节点的同级节点为红色，因此我们应用规则 4a。规则 4a 说我们必须重新着色父节点和父节点的同级节点。因此，节点 7 和 18 都将重新着色，如下所示：

我们还必须检查新节点的父节点的父节点是否为根节点。正如我们在上图中观察到的，新节点的父节点的父节点是根节点，所以我们不需要重新着色它。

步骤 5：下一个元素是 16。由于 16 大于 10 但小于 18 且大于 15，因此节点 16 将放在节点 15 的右侧。树非空；节点 16 应为红色，如下所示：

在上图中，我们可以观察到它违反了父子关系的属性，因为它存在红-红父子关系。我们必须应用一些规则来创建一棵红黑树。由于新节点的父节点为红色，并且新节点的父节点没有同级节点，因此将应用规则 4a。规则 4a 说需要在树上执行一些旋转和重新着色。

由于节点 16 是节点 15 的右侧，而节点 15 的父节点是节点 18。节点 15 是节点 18 的左侧。这里我们有一个LR关系，因此需要执行两次旋转。首先，我们将对节点 15 和 16 执行左旋转，其中节点 16 会向上移动，而节点 15 会向下移动。一旦执行了左旋转，树将如下所示：

在上图中，我们可以观察到存在LL关系。上述树存在红-红冲突，因此我们执行右旋转。当我们执行右旋转时，中位数元素将成为根节点。一旦执行了右旋转，节点 16 将成为根节点，节点 15 和 18 分别将是左子节点和右子节点，如下所示：

旋转后，节点 16 和节点 18 将重新着色；节点 16 的颜色为红色，将变为黑色，节点 18 的颜色为黑色，将变为红色，如下所示：

步骤 6：下一个元素是 30。节点 30 被插入到节点 18 的右侧。由于树非空，因此节点 30 的颜色将为红色。

新节点父节点和父节点同级节点的颜色为红色，因此应用规则 4b。在规则 4b 中，我们只需要重新着色，即不需要进行旋转。父节点（节点 18）和父节点同级节点（节点 15）的颜色都将变为黑色，如下所示：

我们还必须检查新节点的父节点的父节点是否为根节点。新节点的父节点的父节点，即节点 30 是节点 16，而节点 16 不是根节点，因此我们将重新着色节点 16 并将其更改为红色。节点 16 的父节点是节点 10，它不是红色的，所以没有红-红冲突。

步骤 7：下一个元素是 25，我们必须将其插入到树中。由于 25 大于 10、16、18 但小于 30；因此，它将放在节点 30 的左侧。由于树非空，节点 25 应为红色。此处发生红-红冲突，因为新创建节点的父节点为红色。

由于没有父节点的同级节点，因此应用规则 4a，其中会执行旋转和重新着色。首先，我们将执行旋转。由于新创建的节点在其父节点的左侧，而父节点在其父节点的右侧，因此形成了 RL 关系。首先，执行右旋转，节点 25 向上移动，而节点 30 向下移动，如下所示：

第一次旋转后，存在 RR 关系，因此执行左旋转。右旋转后，中位数元素，即 25 将成为根节点；节点 30 将在 25 的右侧，节点 18 将在 25 的左侧。

现在将对节点 25 和 18 执行重新着色；节点 25 变为黑色，节点 18 变为红色。

步骤 8：下一个元素是 40。由于 40 大于 10、16、18、25 和 30，因此节点 40 将放在节点 30 的右侧。由于树非空，节点 40 应为红色。节点 40 和 30 之间存在红-红冲突，因此将应用规则 4b。

由于新节点父节点和父节点同级节点的颜色为红色，因此将执行重新着色。两个节点都将变为黑色，如下所示：

重新着色后，我们还必须检查新节点（即 25）的父节点的父节点，它不是根节点，因此将执行重新着色，节点 25 的颜色将变为红色。

重新着色后，节点 25 和 16 之间发生红-红冲突。现在节点 25 将被视为新节点。由于节点 25 的父节点为红色，而父节点的同级节点为黑色，因此将应用规则 4a。由于 25 在节点 16 的右侧，而 16 在其父节点的右侧，因此存在 RR 关系。在 RR 关系中，执行左旋转。左旋转后，中位数元素 16 将成为根节点，如下所示：

旋转后，对节点 16 和 10 执行重新着色。节点 10 和节点 16 的颜色分别为红色和黑色，如下所示：

步骤 9：下一个元素是 60。由于 60 大于 16、25、30 和 40，因此节点 60 将放在节点 40 的右侧。由于树非空，节点 60 的颜色应为红色。

如上图所示，我们注意到存在红-红冲突。父节点为红色，并且树中不存在父节点的同级节点，因此将应用规则 4a。将执行第一次旋转。节点之间存在 RR 关系，因此将执行左旋转。

当执行左旋转时，节点 40 将向上移动，节点 30 将向下移动，如下所示：

旋转后，对节点 30 和 40 执行重新着色。节点 30 的颜色将变为红色，而节点 40 的颜色将变为黑色。

上述树是一棵红黑树，因为它遵循了所有红黑树的属性。

红黑树中的删除

让我们了解如何从红黑树中删除特定节点。以下是从树中删除特定节点的规则：

步骤 1：首先，我们应用 BST 的删除规则。

步骤 2

情况 1：如果要删除的节点是红色的，则直接删除它。

让我们通过一个例子来理解情况 1。

假设我们要从下图中所示的树中删除节点 30。

最初，我们拥有根节点的地址。首先，我们将应用 BST 来搜索节点。由于 30 大于 10 和 20，这意味着 30 是节点 20 的右子节点。节点 30 是叶节点且为红色，因此直接从树中删除。

如果要删除只有一个子节点的内部节点。首先，将内部节点的值替换为子节点的值，然后直接删除子节点。

让我们再举一个删除内部节点（即节点 20）的例子。

我们不能直接删除内部节点，只能用另一个值替换该节点的值。节点 20 在根节点的右侧，并且只有一个子节点 30。因此，节点 20 被值 30 替换，但节点颜色将保持不变，即黑色。最后，删除节点 20（叶节点）。

如果要删除有两个子节点的内部节点。在这种情况下，我们必须决定用哪个节点的值替换内部节点（要么是左子树，要么是右子树）。我们有两种方法：

中序前驱：我们将用左子树中存在的最大值替换。
中序后继：我们将用右子树中存在的最小值替换。

假设我们要从下图中所示的树中删除节点 30。

节点 30 在根节点的右侧。在这种情况下，我们将使用中序后继。值 38 是右子树中的最小值，因此我们将用 38 替换 30 的值，但节点颜色将保持不变，即红色。替换后，将从树中删除叶节点，即 30。（由于节点 30 是叶节点且为红色，因此我们无需执行任何旋转或重新着色）。

情况 2：如果根节点也是双黑，则直接删除双黑并使其成为单黑。

情况 3：如果双黑节点的同级节点为黑色，且其两个子节点均为黑色。

删除双黑节点。
将节点颜色添加到父节点 (P)。

如果 P 的颜色为红色，则变为黑色。
如果 P 的颜色为黑色，则变为双黑。

双黑节点的同级节点颜色变为红色。
如果仍然出现双黑情况，则将应用其他情况。

让我们通过一个例子来理解这种情况。

假设我们要删除下图中所示的节点 15。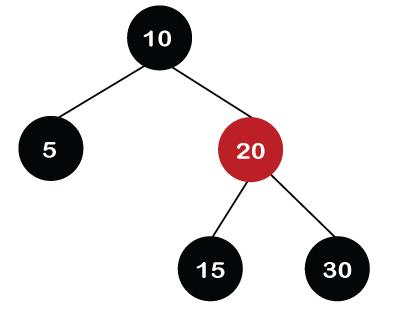

我们不能直接从树中删除节点 15，因为节点 15 是黑色的。节点 15 有两个子节点，它们是 nil。因此，我们将 15 的值替换为 nil 值。由于节点 15 和 nil 节点都是黑色的，替换后节点将变为双黑，如下所示：

在上图中，我们可以观察到双黑节点的同级节点为黑色，并且其子节点也为黑色（nil）。由于双黑节点的同级节点及其子节点都为黑色，因此它无法将其黑色传递给它们中的任何一个。现在，双黑节点的父节点为红色，因此双黑节点将其黑色添加到其父节点。节点 20 的颜色变为黑色，而 nil 节点的颜色变为单黑，如下所示：

将颜色添加到父节点后，双黑节点的同级节点，即节点 30 的颜色变为红色，如下所示：

在上图中，我们可以观察到不再存在双黑问题，并且它仍然是一棵红黑树。

情况 4：如果双黑节点的同级节点为红色。

交换其父节点和同级节点的颜色。
将父节点向双黑节点的方向旋转。
重新应用情况。

让我们通过一个例子来理解这种情况。

假设我们要删除节点 15。

最初，15 被替换为 nil 值。替换后，节点变为双黑。由于双黑节点的同级节点为红色，因此节点 20 的颜色变为红色，节点 30 的颜色变为黑色。

颜色交换完成后，将向双黑节点方向执行旋转。节点 30 将向上移动，节点 20 将向下移动，如下所示：

在上图中，我们可以观察到树中仍然存在双黑情况。它满足情况 3，其中双黑节点的同级节点为黑色，并且两个子节点也为黑色。首先，我们删除双黑节点，并将黑色添加到其父节点。最后，双黑节点的同级节点，即节点 25 的颜色变为红色，如下所示：

在上图中，我们可以观察到双黑情况已得到解决。它也满足红黑树的属性。

情况 5：如果双黑节点的同级节点为黑色，远离双黑节点的同级子节点为红色，但靠近双黑节点的同级子节点为红色。

交换双黑节点同级节点和更靠近双黑节点的同级子节点的颜色。
将同级节点向与双黑节点相反的方向旋转。
应用情况 6。

假设我们要删除下图中所示的节点 1。

首先，我们将 1 的值替换为 nil 值。节点变为双黑，因为节点 1 和 nil 节点都是黑色的。它满足情况 3，即DB 的同级节点为黑色且两个子节点均为黑色。首先，我们删除 nil 节点的双黑。由于 DB 的父节点为黑色，因此当黑色添加到父节点时，它将变为双黑。添加颜色后，双黑节点的同级节点颜色变为红色，如下所示：

我们可以在上图截图中观察到双黑问题仍然存在于树中。因此，我们将重新应用情况。我们将应用情况 5，因为节点 5 的同级节点是节点 30，它是黑色的；节点 30 的子节点，远离开节点 5 的节点为黑色；靠近节点 5 的节点 30 的子节点为红色。在这种情况下，我们首先交换节点 30 和节点 25 的颜色，因此节点 30 的颜色变为红色，节点 25 的颜色变为黑色，如下所示：

一旦完成了节点之间的颜色交换，就需要将同级节点向与双黑节点相反的方向旋转。在此旋转中，节点 30 向下移动，而节点 25 向上移动，如下所示：

正如我们在上图中观察到的，双黑情况仍然存在。因此，我们需要应用情况 6。让我们先看看情况 6 是什么。

情况 6：如果双黑节点的同级节点为黑色，远子节点为红色。

交换父节点和其同级节点的颜色。
将父节点向双黑节点方向旋转。
删除双黑节点。
将红色更改为黑色。

现在我们将应用情况 6 在上述示例中解决双黑情况。

在上例中，双黑节点是节点 5，节点 5 的同级节点是节点 25，它是黑色的。双黑节点的远子节点是节点 30，它为红色，如下所示：

首先，我们将交换父节点及其同级节点的颜色。节点 5 的父节点是节点 10，同级节点是节点 25。两个节点的颜色都是黑色，因此不会发生交换。

在第二步中，我们需要将父节点向双黑节点方向旋转。旋转后，节点 25 将向上移动，而节点 10 将向下移动。旋转完成后，树将如下所示：

在下一步中，我们将从节点 5 中删除双黑，节点 5 将将其黑色传递给远子节点，即节点 30。因此，节点 30 的颜色变为黑色，如下所示：

现在让我们用 Java 编程语言实现红黑树数据结构。

Java 代码

/*
 *  A sample Java Program to Implement the Red-Black Tree Data Structure
 */ 
 // The Scanner class from the util is imported to take input from the user 
 import java.util.Scanner;
 

 // A class named Node_Red_Black_Tree is created whose each object will work as a Node of the Red-Black Tree
 class Node_Red_Black_Tree
 {    

    // Each element of the Red Black tree node has four members.
    // Out of these four members two variables are of Node_Red_Black_Tree class type named left_node_addr and right_node_addr storing the left and right nodes of the previous node 
    Node_Red_Black_Tree left_node_addr, right_node_addr;
    // The node_data Integer variable is used to store the data present in that particular node
    int node_data;
    // The node_data Integer variable is used to store the color of that particular node
    int colour_of_node;
 
     /* Constructor of Node_Red_Black_Tree class */
     public Node_Red_Black_Tree(int thenode_data)
     {
         this( thenode_data, null, null );
     } 
     /* Constructor of Node_Red_Black_Tree class */
     public Node_Red_Black_Tree(int thenode_data, Node_Red_Black_Tree lt, Node_Red_Black_Tree rt)
     {
         left_node_addr = lt;
         right_node_addr = rt;
         node_data = thenode_data;
         colour_of_node = 1;
     }    
 }
 
 // A class named Node_Red_Black_Tree is created whose each object will work as the Red-Black Tree
 class Red_Black_Tree
 {
     private Node_Red_Black_Tree current_node;
     private Node_Red_Black_Tree parent_node;
     private Node_Red_Black_Tree grand_node;
     private Node_Red_Black_Tree great_node;
     private Node_Red_Black_Tree header_node;    
     private static Node_Red_Black_Tree node_null;
     
     /* static block to initialize the data */
     static 
     {
         node_null = new Node_Red_Black_Tree(0);
         node_null.left_node_addr = node_null;
         node_null.right_node_addr = node_null;
     }
     
     // color coding
     /* Black - 1  RED - 0 */
     static final int BLACK = 1;    
     static final int RED   = 0;
 
     /* Constructor of the Red_Black_Tree class  */
     public Red_Black_Tree(int negInf)
     {
         header_node = new Node_Red_Black_Tree(negInf);
         header_node.left_node_addr = node_null;
         header_node.right_node_addr = node_null;
     }
     /* Function to check if tree is empty */
     public boolean isEmpty()
     {
         return header_node.right_node_addr == node_null;
     }
     /* Make the tree logically empty */
     public void makeEmpty()
     {
         header_node.right_node_addr = node_null;
     }
     /* Function to insert item in the Red_Black_Tree class object */
     public void insert(int item )
     {
         current_node = parent_node = grand_node = header_node;
         node_null.node_data = item;
         while (current_node.node_data != item)
         {            
             great_node = grand_node; 
             grand_node = parent_node; 
             parent_node = current_node;
             current_node = item < current_node.node_data ? current_node.left_node_addr : current_node.right_node_addr;
             // Check if two red children and fix if so            
             if (current_node.left_node_addr.colour_of_node == RED && current_node.right_node_addr.colour_of_node == RED)
                 handleReorient( item );
         }
         // Insertion fails if already present
         if (current_node != node_null)
             return;
         current_node = new Node_Red_Black_Tree(item, node_null, node_null);
         // Attach to parent_node
         if (item < parent_node.node_data)
             parent_node.left_node_addr = current_node;
         else
             parent_node.right_node_addr = current_node;        
         handleReorient( item );
     }
     private void handleReorient(int item)
     {
         // Do the colour_of_node flip
         current_node.colour_of_node = RED;
         current_node.left_node_addr.colour_of_node = BLACK;
         current_node.right_node_addr.colour_of_node = BLACK;
 
         if (parent_node.colour_of_node == RED)   
         {
             // Have to rotate
             grand_node.colour_of_node = RED;
             if (item < grand_node.node_data != item < parent_node.node_data)
                 parent_node = rotate( item, grand_node );  // Start dbl rotate
             current_node = rotate(item, great_node );
             current_node.colour_of_node = BLACK;
         }
         // Make root black
         header_node.right_node_addr.colour_of_node = BLACK; 
     }      
     private Node_Red_Black_Tree rotate(int item, Node_Red_Black_Tree parent_node)
     {
         if(item < parent_node.node_data)
             return parent_node.left_node_addr = item < parent_node.left_node_addr.node_data ? rotateWithleft_node_addrChild(parent_node.left_node_addr) : rotateWithright_node_addrChild(parent_node.left_node_addr) ;  
         else
             return parent_node.right_node_addr = item < parent_node.right_node_addr.node_data ? rotateWithleft_node_addrChild(parent_node.right_node_addr) : rotateWithright_node_addrChild(parent_node.right_node_addr);  
     }
     /* Rotate binary tree node with left_node_addr child */
     private Node_Red_Black_Tree rotateWithleft_node_addrChild(Node_Red_Black_Tree k2)
     {
         Node_Red_Black_Tree k1 = k2.left_node_addr;
         k2.left_node_addr = k1.right_node_addr;
         k1.right_node_addr = k2;
         return k1;
     }
     /* Rotate binary tree node with right_node_addr child */
     private Node_Red_Black_Tree rotateWithright_node_addrChild(Node_Red_Black_Tree k1)
     {
         Node_Red_Black_Tree k2 = k1.right_node_addr;
         k1.right_node_addr = k2.left_node_addr;
         k2.left_node_addr = k1;
         return k2;
     }

/* Functions to count number of nodes */
     public int countNodes()
     {
         return countNodes(header_node.right_node_addr);
     }
     private int countNodes(Node_Red_Black_Tree r)
     {
         if (r == node_null)
             return 0;
         else
         {
             int l = 1;
             l += countNodes(r.left_node_addr);
             l += countNodes(r.right_node_addr);
             return l;
         }
     }
     /* Functions to search for an node_data */
     public boolean search(int val)
     {
         return search(header_node.right_node_addr, val);
     }
     private boolean search(Node_Red_Black_Tree r, int val)
     {
         boolean found = false;
         while ((r != node_null) && !found)
         {
             int rval = r.node_data;
             if (val < rval)
                 r = r.left_node_addr;
             else if (val > rval)
                 r = r.right_node_addr;
             else
             {
                 found = true;
                 break;
             }
             found = search(r, val);
         }
         return found;
     }
     /* Function for in order traversal of the Red_Black_Tree class object*/ 
     public void inorder()
     {
         inorder(header_node.right_node_addr);
     }
     private void inorder(Node_Red_Black_Tree r)
     {
         if (r != node_null)
         {
             inorder(r.left_node_addr);
             char c = 'B';
             if (r.colour_of_node == 0)
                 c = 'R';
             System.out.print(r.node_data +""+c+" ");
             inorder(r.right_node_addr);
         }
     }
     /* Function for pre-order traversal of the Red_Black_Tree class object*/ 
     public void preorder()
     {
         preorder(header_node.right_node_addr);
     }
     private void preorder(Node_Red_Black_Tree r)
     {
         if (r != node_null)
         {
             char c = 'B';
             if (r.colour_of_node == 0)
                 c = 'R';
             System.out.print(r.node_data +""+c+" ");
             preorder(r.left_node_addr);             
             preorder(r.right_node_addr);
         }
     }
     /* Function for post-order traversal of the Red_Black_Tree class object*/
     public void postorder()
     {
         postorder(header_node.right_node_addr);
     }
     private void postorder(Node_Red_Black_Tree r)
     {
         if (r != node_null)
         {
             postorder(r.left_node_addr);             
             postorder(r.right_node_addr);
             char c = 'B';
             if (r.colour_of_node == 0)
                 c = 'R';
             System.out.print(r.node_data +""+c+" ");
         }
     }     
 }
 
 /* Class Red_Black_Tree_Run */
class Red_Black_Tree_Run
 {
     public static void main(String[] args)
     {            
        Scanner scannner_object = new Scanner(System.in);
        /* Creating object of RedBlack Tree */
        Red_Black_Tree red_black_tree_object = new Red_Black_Tree(Integer.MIN_VALUE); 
        System.out.println("Red Black Tree Test\n");          
        char ch;
        /*  Perform tree operations  */
        do    
        {
            System.out.println("\nThe options list for Red Black Tree::\n");
            System.out.println("1. To add a new node in the Red-Black Tree");
            System.out.println("2. To search the Red-Black Tree for a node");
            System.out.println("3. To get node count of nodes in Red Black Tree");
            System.out.println("4. To check if the Red_Black_Tree is Empty or not?");
            System.out.println("5. To Clear the Red_Black_Tree.");
 
            int option_list_choice = scannner_object.nextInt();            
            switch (option_list_choice)
            {
            case 1 : 
                System.out.println("Enter integer node_data to insert");
                red_black_tree_object.insert( scannner_object.nextInt() );                     
                break;                          
            case 2 : 
                System.out.println("Enter integer node_data to search");
                System.out.println("Search result : "+ red_black_tree_object.search( scannner_object.nextInt() ));
                break;                                          
            case 3 : 
                System.out.println("Nodes = "+ red_black_tree_object.countNodes());
                break;     
            case 4 : 
                System.out.println("Empty status = "+ red_black_tree_object.isEmpty());
                break;     
            case 5 : 
                System.out.println("\nTree Cleared");
                red_black_tree_object.makeEmpty();
                break;         
            default : 
                System.out.println("Wrong Entry \n ");
                break;    
            }
            
            System.out.print("\nRBT in Post-order: ");
            red_black_tree_object.postorder();
            System.out.print("\nRBT in Pre-order: ");
            red_black_tree_object.preorder();
            System.out.print("\nRBT in In-order: ");
            red_black_tree_object.inorder(); 
 
            System.out.println("\nWanna proceed further(Type y or n)? \n");
            ch = scannner_object.next().charAt(0);                        
        } while (ch == 'Y'|| ch == 'y');               
     }
 }

输出

Red Black Tree Test
The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
10

RBT in Post-order: 10B 
RBT in Pre-order: 10B 
RBT in In-order: 10B 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
18

RBT in Post-order: 18R 10B 
RBT in Pre-order: 10B 18R 
RBT in In-order: 10B 18R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
45

RBT in Post-order: 10R 45R 18B 
RBT in Pre-order: 18B 10R 45R 
RBT in In-order: 10R 18B 45R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
33

RBT in Post-order: 10B 33R 45B 18B 
RBT in Pre-order: 18B 10B 45B 33R 
RBT in In-order: 10B 18B 33R 45B 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
87

RBT in Post-order: 10B 33R 87R 45B 18B 
RBT in Pre-order: 18B 10B 45B 33R 87R 
RBT in In-order: 10B 18B 33R 45B 87R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
90

RBT in Post-order: 10B 33B 90R 87B 45R 18B 
RBT in Pre-order: 18B 10B 45R 33B 87B 90R 
RBT in In-order: 10B 18B 33B 45R 87B 90R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
31

RBT in Post-order: 10B 31R 33B 90R 87B 45R 18B 
RBT in Pre-order: 18B 10B 45R 33B 31R 87B 90R 
RBT in In-order: 10B 18B 31R 33B 45R 87B 90R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
1
Enter integer node_data to insert
77

RBT in Post-order: 10B 31R 33B 77R 90R 87B 45R 18B 
RBT in Pre-order: 18B 10B 45R 33B 31R 87B 77R 90R 
RBT in In-order: 10B 18B 31R 33B 45R 77R 87B 90R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
2
Enter integer node_data to search
18
Search result: true

RBT in Post-order: 10B 31R 33B 77R 90R 87B 45R 18B 
RBT in Pre-order: 18B 10B 45R 33B 31R 87B 77R 90R 
RBT in In-order: 10B 18B 31R 33B 45R 77R 87B 90R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
3
Nodes = 8

RBT in Post-order: 10B 31R 33B 77R 90R 87B 45R 18B 
RBT in Pre-order: 18B 10B 45R 33B 31R 87B 77R 90R 
RBT in In-order: 10B 18B 31R 33B 45R 77R 87B 90R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
4
Empty status = false

RBT in Post-order: 10B 31R 33B 77R 90R 87B 45R 18B 
RBT in Pre-order: 18B 10B 45R 33B 31R 87B 77R 90R 
RBT in In-order: 10B 18B 31R 33B 45R 77R 87B 90R 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
5

Tree Cleared

RBT in Post-order: 
RBT in Pre-order: 
RBT in In-order: 
Wanna proceed further(Type y or n)? 

y

The options list for Red Black Tree::

1. To add a new node in the Red-Black Tree
2. To search the Red-Black Tree for a node
3. To get node count of nodes in Red Black Tree
4. To check if the Red_Black_Tree is Empty or not?
5. To Clear the Red_Black_Tree.
4
Empty status = true

RBT in Post-order: 
RBT in Pre-order: 
RBT in In-order: 
Wanna proceed further(Type y or n)? 

n

现在让我们看看用 C++ 语言实现 RBT 数据结构的示例。

C++ 代码

#include<iostream>

using namespace std;

struct node_of_the_red_black_tree
{
       int key;
       node_of_the_red_black_tree *parent;
       char color;
       node_of_the_red_black_tree *left;
       node_of_the_red_black_tree *right;
};
class Red_Black_Tree
{
      node_of_the_red_black_tree *root;
      node_of_the_red_black_tree *temp_node1;
   public :
      Red_Black_Tree()
      {
              temp_node1=NULL;
              root=NULL;
      }
      void insert_a_node_to_rbt();
      void insert_a_node_to_rbtfix(node_of_the_red_black_tree *);
      void leftrotate_rbt_node(node_of_the_red_black_tree *);
      void rightrotate_rbt_node(node_of_the_red_black_tree *);
      void del_rbt_node();
      node_of_the_red_black_tree* successor(node_of_the_red_black_tree *);
      void del_rbt_nodefix(node_of_the_red_black_tree *);
      void disp();
      void display( node_of_the_red_black_tree *);
      void search_rbt_node();
};
void Red_Black_Tree::insert_a_node_to_rbt()
{
     int init_value,i=0;
     cout<<"\nKey value for the node_of_the_red_black_tree to insert_a_node_to_rbt in RBT: "; cin>>init_value;
     node_of_the_red_black_tree *temp_node,*temp_node1;
     node_of_the_red_black_tree *t=new node_of_the_red_black_tree;
     t->key=init_value;
     t->left=NULL;
     t->right=NULL;
     t->color='r';
     temp_node=root;
     temp_node1=NULL;
     if(root==NULL)
     {
           root=t;
           t->parent=NULL;
     }
     else
     {
         while(temp_node!=NULL)
         {
              temp_node1=temp_node;
              if(temp_node->key<t->key)
                  temp_node=temp_node->right;
              else
                  temp_node=temp_node->left;
         }
         t->parent=temp_node1;
         if(temp_node1->key<t->key)
              temp_node1->right=t;
         else
              temp_node1->left=t;
     }
     insert_a_node_to_rbtfix(t);
}
void Red_Black_Tree::insert_a_node_to_rbtfix(node_of_the_red_black_tree *t)
{
     node_of_the_red_black_tree *u;
     if(root==t)
     {
         t->color='b';
         return;
     }
     while(t->parent!=NULL&&t->parent->color=='r')
     {
           node_of_the_red_black_tree *g=t->parent->parent;
           if(g->left==t->parent)
           {
                        if(g->right!=NULL)
                        {
                              u=g->right;
                              if(u->color=='r')
                              {
                                   t->parent->color='b';
                                   u->color='b';
                                   g->color='r';
                                   t=g;
                              }
                        }
                        else
                        {
                            if(t->parent->right==t)
                            {
                                 t=t->parent;
                                 leftrotate_rbt_node(t);
                            }
                            t->parent->color='b';
                            g->color='r';
                            rightrotate_rbt_node(g);
                        }
           }
           else
           {
                        if(g->left!=NULL)
                        {
                             u=g->left;
                             if(u->color=='r')
                             {
                                  t->parent->color='b';
                                  u->color='b';
                                  g->color='r';
                                  t=g;
                             }
                        }
                        else
                        {
                            if(t->parent->left==t)
                            {
                                   t=t->parent;
                                   rightrotate_rbt_node(t);
                            }
                            t->parent->color='b';
                            g->color='r';
                            leftrotate_rbt_node(g);
                        }
           }
           root->color='b';
     }
}

void Red_Black_Tree::del_rbt_node()
{
     if(root==NULL)
     {
           cout<<"\nEmpty Tree." ;
           return ;
     }
     int x;
     cout<<"\nEnter the key of the node_of_the_red_black_tree to be del_rbt_nodeeted: "; cin>>x;
     node_of_the_red_black_tree *temp_node;
     temp_node=root;
     node_of_the_red_black_tree *y=NULL;
     node_of_the_red_black_tree *temp_node1=NULL;
     int found=0;
     while(temp_node!=NULL&&found==0)
     {
           if(temp_node->key==x)
               found=1;
           if(found==0)
           {
                 if(temp_node->key<x) temp_node=temp_node->right;
                 else
                    temp_node=temp_node->left;
           }
     }
     if(found==0)
     {
            cout<<"\nElement Not Found.";
            return ;
     }
     else
     {
         cout<<"\ndel_rbt_nodeeted Element: "<<temp_node->key;
         cout<<"\nColour: "; if(temp_node->color=='b')
     cout<<"Black\n";
    else
     cout<<"Red\n"; if(temp_node->parent!=NULL)
               cout<<"\nParent: "<<temp_node->parent->key;
         else
               cout<<"\nno parent node_of_the_red_black_tree present "; if(temp_node->right!=NULL)
               cout<<"\nRight Child: "<<temp_node->right->key;
         else
               cout<<"\nno right child node_of_the_red_black_tree present. "; if(temp_node->left!=NULL)
               cout<<"\nLeft Child: "<<temp_node->left->key;
         else
               cout<<"\nno left child node_of_the_red_black_tree present.  ";
         cout<<"\nnode_of_the_red_black_tree del_rbt_nodeeted."; if(temp_node->left==NULL||temp_node->right==NULL)
              y=temp_node;
         else
              y=successor(temp_node);
         if(y->left!=NULL)
              temp_node1=y->left;
         else
         {
              if(y->right!=NULL)
                   temp_node1=y->right;
              else
                   temp_node1=NULL;
         }
         if(temp_node1!=NULL)
              temp_node1->parent=y->parent;
         if(y->parent==NULL)
              root=temp_node1;
         else
         {
             if(y==y->parent->left)
                y->parent->left=temp_node1;
             else
                y->parent->right=temp_node1;
         }
         if(y!=temp_node)
         {
             temp_node->color=y->color;
             temp_node->key=y->key;
         }
         if(y->color=='b')
             del_rbt_nodefix(temp_node1);
     }
}

void Red_Black_Tree::del_rbt_nodefix(node_of_the_red_black_tree *temp_node)
{
    node_of_the_red_black_tree *s;
    while(temp_node!=root&&temp_node->color=='b')
    {
          if(temp_node->parent->left==temp_node)
          {
                  s=temp_node->parent->right;
                  if(s->color=='r')
                  {
                         s->color='b';
                         temp_node->parent->color='r';
                         leftrotate_rbt_node(temp_node->parent);
                         s=temp_node->parent->right;
                  }
                  if(s->right->color=='b'&&s->left->color=='b')
                  {
                         s->color='r';
                         temp_node=temp_node->parent;
                  }
                  else
                  {
                      if(s->right->color=='b')
                      {
                             s->left->color=='b';
                             s->color='r';
                             rightrotate_rbt_node(s);
                             s=temp_node->parent->right;
                      }
                      s->color=temp_node->parent->color;
                      temp_node->parent->color='b';
                      s->right->color='b';
                      leftrotate_rbt_node(temp_node->parent);
                      temp_node=root;
                  }
          }
          else
          {
                  s=temp_node->parent->left;
                  if(s->color=='r')
                  {
                        s->color='b';
                        temp_node->parent->color='r';
                        rightrotate_rbt_node(temp_node->parent);
                        s=temp_node->parent->left;
                  }
                  if(s->left->color=='b'&&s->right->color=='b')
                  {
                        s->color='r';
                        temp_node=temp_node->parent;
                  }
                  else
                  {
                        if(s->left->color=='b')
                        {
                              s->right->color='b';
                              s->color='r';
                              leftrotate_rbt_node(s);
                              s=temp_node->parent->left;
                        }
                        s->color=temp_node->parent->color;
                        temp_node->parent->color='b';
                        s->left->color='b';
                        rightrotate_rbt_node(temp_node->parent);
                        temp_node=root;
                  }
          }
       temp_node->color='b';
       root->color='b';
    }
}

void Red_Black_Tree::leftrotate_rbt_node(node_of_the_red_black_tree *temp_node)
{
     if(temp_node->right==NULL)
           return ;
     else
     {
           node_of_the_red_black_tree *y=temp_node->right;
           if(y->left!=NULL)
           {
                  temp_node->right=y->left;
                  y->left->parent=temp_node;
           }
           else
                  temp_node->right=NULL;
           if(temp_node->parent!=NULL)
                y->parent=temp_node->parent;
           if(temp_node->parent==NULL)
                root=y;
           else
           {
               if(temp_node==temp_node->parent->left)
                       temp_node->parent->left=y;
               else
                       temp_node->parent->right=y;
           }
           y->left=temp_node;
           temp_node->parent=y;
     }
}
void Red_Black_Tree::rightrotate_rbt_node(node_of_the_red_black_tree *temp_node)
{
     if(temp_node->left==NULL)
          return ;
     else
     {
         node_of_the_red_black_tree *y=temp_node->left;
         if(y->right!=NULL)
         {
                  temp_node->left=y->right;
                  y->right->parent=temp_node;
         }
         else
                 temp_node->left=NULL;
         if(temp_node->parent!=NULL)
                 y->parent=temp_node->parent;
         if(temp_node->parent==NULL)
               root=y;
         else
         {
             if(temp_node==temp_node->parent->left)
                   temp_node->parent->left=y;
             else
                   temp_node->parent->right=y;
         }
         y->right=temp_node;
         temp_node->parent=y;
     }
}

node_of_the_red_black_tree* Red_Black_Tree::successor(node_of_the_red_black_tree *temp_node)
{
      node_of_the_red_black_tree *y=NULL;
     if(temp_node->left!=NULL)
     {
         y=temp_node->left;
         while(y->right!=NULL)
              y=y->right;
     }
     else
     {
         y=temp_node->right;
         while(y->left!=NULL)
              y=y->left;
     }
     return y;
}

void Red_Black_Tree::disp()
{
     display(root);
}
void Red_Black_Tree::display(node_of_the_red_black_tree *temp_node)
{
     if(root==NULL)
     {
          cout<<"\nEmpty Tree.";
          return ;
     }
     if(temp_node!=NULL)
     {
                cout<<"\n\t node_of_the_red_black_tree: ";
                cout<<"\n Key: "<<temp_node->key;
                cout<<"\n Colour: "; if(temp_node->color=='b')
     cout<<"Black";
    else
     cout<<"Red"; if(temp_node->parent!=NULL)
                       cout<<"\n Parent: "<<temp_node->parent->key;
                else
                       cout<<"\n no parent node_of_the_red_black_tree present "; if(temp_node->right!=NULL)
                       cout<<"\n Right Child: "<<temp_node->right->key;
                else
                       cout<<"\n no right child node_of_the_red_black_tree present. "; if(temp_node->left!=NULL)
                       cout<<"\n Left Child: "<<temp_node->left->key;
                else
                       cout<<"\n no left child node_of_the_red_black_tree present.  ";
                cout<<endl; if(temp_node->left)
    {
                 cout<<"\n\nLeft:\n"; display(temp_node->left);
    }
    /*else
     cout<<"\nNo Left Child.\n";*/ if(temp_node->right)
    {
     cout<<"\n\nRight:\n"; display(temp_node->right);
    }
    /*else
     cout<<"\nNo Right Child.\n"*/
     }
}
void Red_Black_Tree::search_rbt_node()
{
     if(root==NULL)
     {
           cout<<"\nEmpty Tree\n" ;
           return  ;
     }
     int x;
     cout<<"\n Enter key of the node_of_the_red_black_tree to be search_rbt_nodeed: "; cin>>x;
     node_of_the_red_black_tree *temp_node=root;
     int found=0;
     while(temp_node!=NULL&& found==0)
     {
            if(temp_node->key==x)
                found=1;
            if(found==0)
            {
                 if(temp_node->key<x) temp_node=temp_node->right;
                 else
                      temp_node=temp_node->left;
            }
     }
     if(found==0)
          cout<<"\nElement Not Found.";
     else
     {
                cout<<"\n\t FOUND node_of_the_red_black_tree: ";
                cout<<"\n Key: "<<temp_node->key;
                cout<<"\n Colour: "; if(temp_node->color=='b')
     cout<<"Black";
    else
     cout<<"Red"; if(temp_node->parent!=NULL)
                       cout<<"\n Parent: "<<temp_node->parent->key;
                else
                       cout<<"\n no parent node_of_the_red_black_tree present"; if(temp_node->right!=NULL)
                       cout<<"\n Right Child: "<<temp_node->right->key;
                else
                       cout<<"\n no right child node_of_the_red_black_tree present. "; if(temp_node->left!=NULL)
                       cout<<"\n Left Child: "<<temp_node->left->key;
                else
                       cout<<"\n no left child node_of_the_red_black_tree present";
                cout<<endl;

     }
}
int main()
{
    int ch,y=0;
    Red_Black_Tree obj;
    do
    {
                cout<<"\nThe options list for Red Black Tree::" ;
                cout<<"\n1. To add a new node_of_the_red_black_tree in the Red-Black Tree";
                cout<<"\n2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree";
                cout<<"\n3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree";
                cout<<"\n4. To display all the node_of_the_red_black_trees of the Red-Black Tree ";
                cout<<"\n5. To exit the code execution." ;
                cout<<"\nInput: ";
                cin>>ch;
                switch(ch)
                {
                          case 1 : obj.insert_a_node_to_rbt();
                                   cout<<"\nNew node_of_the_red_black_tree added.\n";
                                   break;
                          case 2 : 
                                obj.search_rbt_node();
                                   break;
                          case 3 : 

                                    obj.del_rbt_node();
                                   break;
                          case 4 : obj.disp();
                                   break;
                          case 5 : y=1;
                                   break;
                          default : cout<<"\nEnter a Valid Choice.";
                }
                cout<<endl;

    }while(y!=1);
    return 0;
}

输出

The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 1

Key value for the node_of_the_red_black_tree to insert_a_node_to_rbt in RBT: 12

New node_of_the_red_black_tree added.


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 1

Key value for the node_of_the_red_black_tree to insert_a_node_to_rbt in RBT: 45

New node_of_the_red_black_tree added.


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 1

Key value for the node_of_the_red_black_tree to insert_a_node_to_rbt in RBT: 23

New node_of_the_red_black_tree added.


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 1

Key value for the node_of_the_red_black_tree to insert_a_node_to_rbt in RBT: 98

New node_of_the_red_black_tree added.


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 4

     node_of_the_red_black_tree: 
 Key: 23
 Colour: Black
 Parent: 12
 Right Child: 45
 Left Child: 12


Left:

     node_of_the_red_black_tree: 
 Key: 12
 Colour: Black
 Parent: 23
 no right child node_of_the_red_black_tree present. 
 no left child node_of_the_red_black_tree present.  


Right:

     node_of_the_red_black_tree: 
 Key: 45
 Colour: Black
 Parent: 23
 Right Child: 98
 no left child node_of_the_red_black_tree present.  


Right:

     node_of_the_red_black_tree: 
 Key: 98
 Colour: Red
 Parent: 45
 no right child node_of_the_red_black_tree present. 
 no left child node_of_the_red_black_tree present.  


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 2

 Enter key of the node_of_the_red_black_tree to be search_rbt_nodeed: 98

     FOUND node_of_the_red_black_tree: 
 Key: 98
 Colour: Red
 Parent: 45
 no right child node_of_the_red_black_tree present. 
 no left child node_of_the_red_black_tree present


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 3

Enter the key of the node_of_the_red_black_tree to be del_rbt_nodeeted: 45

del_rbt_nodeeted Element: 45
Colour: Black

Parent: 23
Right Child: 98
no left child node_of_the_red_black_tree present.  
node_of_the_red_black_tree del_rbt_nodeeted.

The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 4

     node_of_the_red_black_tree: 
 Key: 23
 Colour: Black
 Parent: 12
 Right Child: 98
 Left Child: 12


Left:

     node_of_the_red_black_tree: 
 Key: 12
 Colour: Black
 Parent: 23
 no right child node_of_the_red_black_tree present. 
 no left child node_of_the_red_black_tree present.  


Right:

     node_of_the_red_black_tree: 
 Key: 98
 Colour: Red
 Parent: 23
 no right child node_of_the_red_black_tree present. 
 no left child node_of_the_red_black_tree present.  


The options list for Red Black Tree::
1. To add a new node_of_the_red_black_tree in the Red-Black Tree
2. To search_rbt_node the Red-Black Tree for a node_of_the_red_black_tree
3. To del_rbt_nodeete an existing Red-Black tree node_of_the_red_black_tree
4. To display all the node_of_the_red_black_trees of the Red-Black Tree 
5. To exit the code execution.
Input: 5

下一个主题Aa-tree-in-data-structure

← 上一个下一个 →

我们提供所有技术（如 Java 教程、Android、Java 框架）的教程和面试问题

联系信息

G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India

hr@tpointtech.com

+91-9599086977

关注我们

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

数据结构中的红黑树

红黑树的性质

每棵 AVL 树都可以是红黑树吗？

红黑树中的插入

红黑树中的删除

Java 代码

C++ 代码

相关帖子

二叉树

树 (数据结构)

B 树

数据结构中的 AA 树

二叉搜索树

B+ 树

AVL 树

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器