AVL 树

AVL 树由 GM Adelson - Velsky 和 EM Landis 于 1962 年发明。该树以其发明者的名字命名为 AVL。

AVL 树可以定义为一种高度平衡的二叉搜索树，其中每个节点都关联一个平衡因子，该因子是通过从其左子树的高度中减去其右子树的高度来计算的。

如果每个节点的平衡因子都在 -1 到 1 之间，则该树被认为是平衡的；否则，该树将不平衡，需要进行平衡。

平衡因子 (k) = 高度 (左(k)) - 高度 (右(k))

如果任何节点的平衡因子为 1，则表示左子树比右子树高一级。

如果任何节点的平衡因子为 0，则表示左子树和右子树的高度相等。

如果任何节点的平衡因子为 -1，则表示左子树比右子树低一级。

下图所示为一棵 AVL 树。我们可以看到，每个节点的平衡因子都在 -1 和 +1 之间。因此，它是一棵 AVL 树的例子。

复杂度

AVL 树上的操作

由于 AVL 树也是一种二叉搜索树，因此所有操作的执行方式与二叉搜索树中的操作相同。搜索和遍历不会导致 AVL 树属性的违反。但是，插入和删除可能会违反此属性，因此需要重新审视。

为什么选择 AVL 树？

AVL 树通过防止二叉搜索树变得倾斜来控制其高度。高度为 h 的二叉搜索树的各项操作所需时间为 **O(h)**。但是，如果 BST 变得倾斜（即最坏情况），则可以扩展到 **O(n)**。通过将此高度限制为 log n，AVL 树对每次操作施加了 **O(log n)** 的上限，其中 n 是节点数。

AVL 旋转

只有当平衡因子不是 **-1、0 或 1** 时，我们才在 AVL 树中执行旋转。基本上有四种类型的旋转，如下所示：

1. LL 旋转：插入的节点位于 A 的左子树的左子树中
2. RR 旋转：插入的节点位于 A 的右子树的右子树中
3. LR 旋转：插入的节点位于 A 的左子树的右子树中
4. RL 旋转：插入的节点位于 A 的右子树的左子树中

其中节点 A 是平衡因子不为 -1、0、1 的节点。

前两种旋转 LL 和 RR 是单次旋转，后两种旋转 LR 和 RL 是双次旋转。要使树不平衡，最小高度必须至少为 2。让我们来理解每种旋转。

1. RR 旋转

当 BST 由于节点插入到 A 的右子树的右子树中而不平衡时，我们将执行 RR 旋转。 RR 旋转是一种逆时针旋转，应用于平衡因子为 -2 的节点下方的边。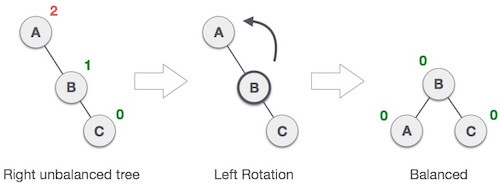

在上面的示例中，节点 A 的平衡因子为 -2，因为节点 C 被插入到 A 的右子树的右子树中。我们在 A 下方的边上执行 RR 旋转。

2. LL 旋转

当 BST 由于节点插入到 C 的左子树的左子树中而不平衡时，我们将执行 LL 旋转。 LL 旋转是一种顺时针旋转，应用于平衡因子为 2 的节点下方的边。

在上面的示例中，节点 C 的平衡因子为 2，因为节点 A 被插入到 C 的左子树的左子树中。我们在 A 下方的边上执行 LL 旋转。

3. LR 旋转

双旋转比上面解释的单次旋转要复杂一些。LR 旋转 = RR 旋转 + LL 旋转，即首先对子树执行 RR 旋转，然后对整个树执行 LL 旋转，整个树是指从插入节点的路径开始的第一个平衡因子不为 -1、0 或 1 的节点。

让我们非常清楚地理解每一步。

国家	操作
	节点 B 已插入到 C 的左子树的右子树中，因此 C 成为一个不平衡节点，平衡因子为 2。这种情况是 LR 旋转，其中：插入的节点位于 C 的左子树的右子树中。
	由于 LR 旋转 = RR + LL 旋转，因此首先对以 A 为根的子树执行 RR（逆时针）旋转。通过执行 RR 旋转，节点 **A** 已成为 **B** 的左子树。
	执行 RR 旋转后，节点 C 仍然不平衡，即平衡因子为 2，因为插入的节点 A 在 C 的左左子树中。
	现在我们对整个树（即节点 C）执行 LL 顺时针旋转。节点 **C** 现在已成为节点 B 的右子树，A 是 B 的左子树。
	现在每个节点的平衡因子都是 -1、0 或 1，即 BST 现在是平衡的。

4. RL 旋转

如前所述，双旋转比上面解释的单次旋转要复杂一些。 RL 旋转 = LL 旋转 + RR 旋转，即首先对子树执行 LL 旋转，然后对整个树执行 RR 旋转，整个树是指从插入节点的路径开始的第一个平衡因子不为 -1、0 或 1 的节点。

国家	操作
	节点 **B** 已插入到 A 的右子树的左子树中，因此 A 成为一个不平衡节点，平衡因子为 -2。这种情况是 RL 旋转，其中：插入的节点位于 A 的右子树的左子树中。
	由于 RL 旋转 = LL 旋转 + RR 旋转，因此首先对以 **C** 为根的子树执行 LL（顺时针）旋转。通过执行 RR 旋转，节点 **C** 已成为 **B** 的右子树。
	执行 LL 旋转后，节点 **A** 仍然不平衡，即平衡因子为 -2，这是因为节点 A 的右子树的右子树。
	现在我们对整个树（即节点 A）执行 RR 旋转（逆时针旋转）。节点 **C** 现在已成为节点 B 的右子树，节点 A 已成为节点 B 的左子树。
	现在每个节点的平衡因子都是 -1、0 或 1，即 BST 现在是平衡的。

问：构造一个包含以下元素的 AVL 树

H, I, J, B, A, E, C, F, D, G, K, L

1. 插入 H, I, J

插入上述元素后，特别是在 H 的情况下，BST 会变得不平衡，因为 H 的平衡因子为 -2。由于 BST 是右倾斜的，我们将对节点 H 执行 RR 旋转。

最终的平衡树是

2. 插入 B, A

插入上述元素后，特别是在 A 的情况下，BST 会变得不平衡，因为 H 和 I 的平衡因子为 2，我们考虑从最后一个插入的节点（即 H）开始。由于从 H 开始的 BST 是左倾斜的，我们将对节点 H 执行 LL 旋转。

最终的平衡树是

3. 插入 E

插入 E 后，BST 会变得不平衡，因为 I 的平衡因子为 2。由于从 E 到 I 的路径表明它被插入到 I 的右子树的左子树中，我们将对节点 I 执行 LR 旋转。LR = RR + LL 旋转。

3 a) 我们首先对节点 B 执行 RR 旋转。

RR 旋转后的树形是

3b) 我们首先对节点 I 执行 LL 旋转。

LL 旋转后的平衡树形是

4. 插入 C, F, D

插入 C、F、D 后，BST 会变得不平衡，因为 B 和 H 的平衡因子为 -2。由于从 D 到 B 的路径表明它被插入到 B 的左子树的右子树中，我们将对节点 I 执行 RL 旋转。RL = LL + RR 旋转。

4a) 我们首先对节点 E 执行 LL 旋转。

LL 旋转后的树形是

4b) 然后我们对节点 B 执行 RR 旋转。

RR 旋转后的平衡树形是

5. 插入 G

插入 G 后，BST 会变得不平衡，因为 H 的平衡因子为 2。由于从 G 到 H 的路径表明它被插入到 H 的右子树的左子树中，我们将对节点 I 执行 LR 旋转。LR = RR + LL 旋转。

5 a) 我们首先对节点 C 执行 RR 旋转。

RR 旋转后的树形是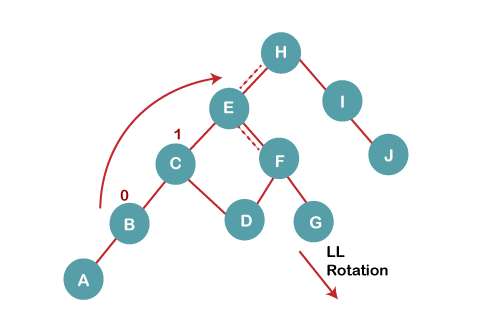

5 b) 然后我们对节点 H 执行 LL 旋转。

LL 旋转后的平衡树形是

6. 插入 K

插入 K 后，BST 会变得不平衡，因为 I 的平衡因子为 -2。由于从 I 到 K 的 BST 是右倾斜的，因此我们将对节点 I 执行 RR 旋转。

RR 旋转后的平衡树形是

7. 插入 L

插入 L 后，树仍然是平衡的，因为每个节点的平衡因子现在都是 -1、0 或 +1。因此，该树是一棵平衡的 AVL 树。