桶排序算法（含Python/Java/C/C++程序）

2025年7月15日 | 阅读13分钟

桶排序是一种排序算法，它将元素分成多个组，称为桶。桶排序中的元素首先被均匀地分成称为桶的组，然后使用任何其他排序算法进行排序。之后，按排序方式收集元素。

算法

Bucket Sort(A[])  
Let B[0....n-1] be a new array  
n=length[A]  
for i=0 to n-1  
make B[i] an empty list  
for i=1 to n  
do insert A[i] into list B[n * a[i]]  
for i=0 to n-1  
do sort list B[i] with insertion-sort  
Concatenate lists B[0], B[1],........, B[n-1] together in order  
End  

桶排序的步骤

步骤1：创建s个大小的空列表（或桶），其中s是数组的大小。

步骤2：将inputArr[j]插入到bucket[s * inputArr[j]]中

步骤3：使用插入排序对各个桶进行排序。

步骤4：按顺序从桶中收集已排序的元素，并将它们存储在输入数组中。

步骤5：打印已排序的列表。

桶排序算法的工作原理

我们将使用散布-收集方法来理解桶排序算法。在此方法中，给定的元素首先被分发到桶中。分发工作完成后，每个桶中的元素使用插入排序算法进行排序。最后，按顺序收集已排序的元素。

让我们采用一个未排序的数组来理解桶排序的过程。通过示例理解桶排序会更容易。

我们将输入数组设为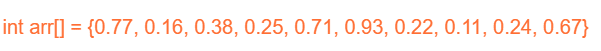

Bucket Sort Algorithm (With Program in Python/Java/C/C++)

现在，我们创建一个大小为10的数组，其中每个元素都充当一个桶。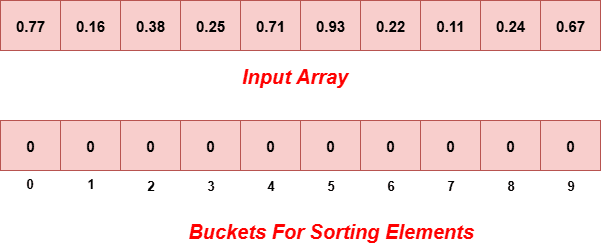

现在，我们需要根据范围将元素分类到桶中。例如，如果我们想插入元素0.77，那么我们将0.77乘以10，即0.77 × 10 = 7.7。现在，取7.7的整数部分，即7。因此，0.77落在索引为7的桶中。同样，我们可以放置输入数组中的其他元素。添加所有数组元素后，桶将如下所示。

现在，我们对每个桶应用插入排序。之后，桶将如下所示。

最后，我们按顺序从桶中收集已排序的元素，并将它们存储在输入数组中。现在，输入数组将如下所示。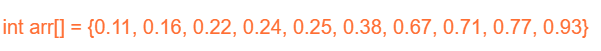

我们可以看到数组已完全排序。

Python/Java/C/C++/C# 中桶排序的实现

Python 程序

def insertion_sort(bukt):
    for j in range(1, len(bukt)):
        val = bukt[j]
        k = j - 1
        while k >= 0 and bukt[k] > val:
            bukt[k + 1] = bukt[k]
            k -= 1
        bukt[k + 1] = val
def bucket_sort(inputArr):
    s = len(inputArr)
    bucketArr = [[] for _ in range(s)]
    # Placing the array elements into various buckets
    for j in inputArr:
        bi = int(s * j)
        bucketArr[bi].append(j)
    # Sorting every bucket with the help of Insertion Sort
    for bukt in bucketArr:
        insertion_sort(bukt)
    # Concatenating all of the sorted buckets into the input array
    idx = 0
    for bukt in bucketArr:
        for j in bukt:
            inputArr[idx] = j
            idx += 1
inputArr = [0.77, 0.16, 0.38, 0.25, 0.71, 0.93, 0.22, 0.11, 0.24, 0.67]
print("Array before sorting is:")
print(" ".join(map(str, inputArr)))
bucket_sort(inputArr)
print("Array after sorting is:")
print(" ".join(map(str, inputArr)))

立即执行

Java 程序

import java.util.List;
import java.util.ArrayList;
public class Main {
    // Insertion sort method for sorting individual buckets
    public static void insertionSort(List<Float> bukt) {
        for (int j = 1; j < bukt.size(); ++j) {
            float val = bukt.get(j);
            int k = j - 1;
            while (k >= 0 && bukt.get(k) > val) {
                bukt.set(k + 1, bukt.get(k));
                k = k - 1;
            }
            bukt.set(k + 1, val);
        }
    }
    // Method to do sorting of inputArr[] of the size s using Bucket Sort
    public static void bucketSort(float[] inputArr) {
        int s = inputArr.length;
        // Creating s empty buckets
        List<Float>[] bucketArr = new ArrayList[s];
        for (int i = 0; i < s; i++) {
            bucketArr[i] = new ArrayList<>();
        }
        // Putting input array elements into various buckets
        for (int j = 0; j < s; j++) {
            int bi = (int) (s * inputArr[j]);
            bucketArr[bi].add(inputArr[j]);
        }
        // Sorting every bucket with the help of Insertion Sort
        for (int j = 0; j < s; j++) {
            insertionSort(bucketArr[j]);
        }
        // Concatenating all of the buckets into the input array
        int idx = 0;
        for (int j = 0; j < s; j++) {
            for (int k = 0; k < bucketArr[j].size(); k++) {
                inputArr[idx] = bucketArr[j].get(k);
				idx = idx + 1;
            }
        }
    }
    // Main Method
    public static void main(String[] args) {
        float[] inputArr = {0.77f, 0.16f, 0.38f, 0.25f, 0.71f, 0.93f, 0.22f, 0.11f, 0.24f, 0.67f};
        System.out.println("Array before sorting is:");
        for (float val : inputArr) {
            System.out.print(val + " ");
        }
        System.out.println();
        bucketSort(inputArr);
        System.out.println("Array after sorting is:");
        for (float val : inputArr) {
            System.out.print(val + " ");
        }
    }

编译并运行

C++ 程序

#include <iostream>
#include <vector>
using namespace std;
// Insertion sort method for sorting individual buckets
void insertionSort(vector<float>& bukt) {
    for (int j = 1; j < bukt.size(); ++j) {
            float val = bukt[j];
            int k = j - 1;
            while (k >= 0 && bukt[k] > val) {
                bukt[k + 1] = bukt[k];
                k = k - 1;
            }
            bukt[k + 1] = val;
        }
}
// Method to do sorting of inputArr[] of the size s using Bucket Sort
void bucketSort(float inputArr[], int s) {
    // Creating s empty buckets
    vector<float> bucketArr[s];
    // Putting input array elements into various buckets
    for (int j = 0; j < s; j++) {
        int bi = s * inputArr[j];
        bucketArr[bi].push_back(inputArr[j]);
    }
    // Sorting every bucket with the help of Insertion Sort
    for (int j = 0; j < s; j++) {
        insertionSort(bucketArr[j]);
    }
    // Concatenating all of the buckets into the input array
    int idx = 0;
    for (int j = 0; j < s; j++) {
        for (int k = 0; k < bucketArr[j].size(); k++) {
            inputArr[idx] = bucketArr[j][k];
			idx = idx + 1;
        }
    }
}
// Main function
int main() {
    float inputArr[] = {0.77f, 0.16f, 0.38f, 0.25f, 0.71f, 0.93f, 0.22f, 0.11f, 0.24f, 0.67f};
    int s = sizeof(inputArr) / sizeof(inputArr[0]);
    cout <<"Array before sorting is: \n";
    for (int j = 0; j < s; j++) {
        cout << inputArr[j] << " ";
    }
    cout<<endl;
    bucketSort(inputArr, s);
    cout <<"Array after sorting is: \n";
    for (int j = 0; j < s; j++) {
        cout << inputArr[j] << " ";
    }
    return 0;
}

编译并运行

C 语言程序

#include <stdio.h>
#include <stdlib.h>
struct Node {
  float val;
  struct Node *nxt;
};
void BucketSort(float inputArr[], int s);
struct Node *InsertionSort(struct Node *l);
void displayArr(float inputArr[], int s); // to display the array elements
int getBucketIndex(int val, int s);
// Sorting function
void BucketSort(float inputArr[], int s) {
  int j, k;
  struct Node **bucketArr;
  // Creating buckets and allocating memory size
  bucketArr = (struct Node **)malloc(sizeof(struct Node *) * s);
  // Initialize empty buckets
  for (j = 0; j < s; j++) {
    bucketArr[j] = NULL;
  }
  // Filling the buckets with elements
  for (j = 0; j < s; j++) {
    struct Node *curr;
    int idx = getBucketIndex(inputArr[j], s);
    curr = (struct Node *)malloc(sizeof(struct Node));
    curr->val = inputArr[j];
    curr->nxt = bucketArr[idx];
    bucketArr[idx] = curr;
  }
  // Sorting the elements of each bucket
  for (j = 0; j < s; j++) {
    bucketArr[j] = InsertionSort(bucketArr[j]);
  }
  // Putting sorted elements into the input array
  for (k = 0, j = 0; j < s; ++j) {
    struct Node *node;
    node = bucketArr[j];
    while (node) {
      inputArr[k] = node->val;
      node = node->nxt;
	  k = k + 1;
    }
  }
  return;
}
// Function to do sorting of elements of each bucket
struct Node *InsertionSort(struct Node *l) {
  struct Node *kl, *ndeList;
  if (l == 0 || l->nxt == 0) {
    return l;
  }
  ndeList = l;
  kl = l->nxt;
  ndeList->nxt = 0;
  while (kl != 0) {
    struct Node *ptr;
    if (ndeList->val > kl->val) {
      struct Node *temp;
      temp = kl;
      kl = kl->nxt;
      temp->nxt = ndeList;
      ndeList = temp;
      continue;
    }
    for (ptr = ndeList; ptr->nxt != 0; ptr = ptr->nxt) {
      if (ptr->nxt->val > kl->val)
        break;
    }
    if (ptr->nxt != 0) {
      struct Node *temp;
      temp = kl;
      kl = kl->nxt;
      temp->nxt = ptr->nxt;
      ptr->nxt = temp;
      continue;
    } else {
      ptr->nxt = kl;
      kl = kl->nxt;
      ptr->nxt->nxt = 0;
      continue;
    }
  }
  return ndeList;
}
int getBucketIndex(int val, int s) {
  return val / s;
}
void displayArr(float inputArr[], int s) {
  int j;
  for (int j = 0; j < s; j++) {
    printf("%0.2f ", inputArr[j]);
  }
  printf("\n");
}
// Main function
int main(void) { 
  float inputArr[] = {0.77f, 0.16f, 0.38f, 0.25f, 0.71f, 0.93f, 0.22f, 0.11f, 0.24f, 0.67f};
  int s = sizeof(inputArr) / sizeof(inputArr[0]);
  printf("Array before sorting is: \n ");
  displayArr(inputArr, s);
  BucketSort(inputArr, s);
  printf("Array after sorting is: \n ");
  displayArr(inputArr, s);
  return 0;
}

编译并运行

C# 程序

using System;
using System.Collections.Generic;
class BucketSort {
    // Insertion sort method for sorting individual buckets
    static void InsertionSort(List<float> bukt)  {
        for (int j = 1; j < bukt.Count; ++j)  {
            float val = bukt[j];
            int k = j - 1;
            while (k >= 0 && bukt[k] > val)  {
                bukt[k + 1] = bukt[k];
                k = k - 1;
            }
            bukt[k + 1] = val;
        }
    }
    // Method to do sorting of inputArr[] of the size s using Bucket Sort
    static void BucktSort(float[] inputArr, int s) {
        // Creating s empty buckets
        List<float>[] bucketArr = new List<float>[s];
        for (int j = 0; j < s; j++) {
            bucketArr[j] = new List<float>();
        }
        // Putting  input array elements into various buckets
        for (int j = 0; j < s; j++) {
	        int bi = (int)(s * inputArr[j]);
	        bucketArr[bi].Add(inputArr[j]);
    	}
        // Sorting every bucket with the help of Insertion Sort
        for (int j = 0; j < s; j++) {
            InsertionSort(bucketArr[j]);
        }
        // Concatenating all of the buckets into the input array
        int idx = 0;
	    for (int j = 0; j < s; j++) {
	        for (int k = 0; k < bucketArr[j].Count; k++) {
	            inputArr[idx] = bucketArr[j][k];
				idx = idx + 1;
	        }
	    }
    }
    // Main Method
    static void Main(string[] args) {
        float[] inputArr = {0.77f, 0.16f, 0.38f, 0.25f, 0.71f, 0.93f, 0.22f, 0.11f, 0.24f, 0.67f};
        int s = inputArr.Length;   
        Console.WriteLine("Array before sorting is: ");
        foreach (float val in inputArr)  {
            Console.Write(val + " ");
        } 
        BucktSort(inputArr, s);
        Console.WriteLine();
        Console.WriteLine("Array after sorting is: ");
        foreach (float val in inputArr) {
            Console.Write(val + " ");
        }
    }
}

编译并运行

输出

Array before sorting is:
0.77 0.16 0.38 0.25 0.71 0.93 0.22 0.11 0.24 0.67
Array after sorting is:
0.11 0.16 0.22 0.24 0.25 0.38 0.67 0.71 0.77 0.93

复杂度分析

现在，让我们看看桶排序在最佳情况、平均情况和最坏情况下的时间复杂度。我们还将查看桶排序的空间复杂度。

时间复杂度

最佳情况复杂度：最佳情况发生在不需要排序时，即输入数组已排序。在桶排序中，当元素在桶中均匀分布时，会出现最佳情况。当元素已经在桶中排序时，复杂度会更好。

假设有人使用插入排序来对桶元素进行排序。在这种情况下，总时间复杂度将是线性的，即 O(n + k)，其中 O(n) 用于创建桶，O(k) 用于使用在最佳情况下具有线性时间复杂度的算法对桶元素进行排序。桶排序的最佳情况时间复杂度为O(n + k)。

平均情况复杂度：平均情况发生在数组元素杂乱无章时，即既不完全降序也不完全升序。桶排序的平均情况时间复杂度为O(n + K)。

最坏情况复杂度：当一个桶接收输入数组的所有元素时，就会发生最坏情况。在这种情况下，插入排序将在数组的所有元素上运行。因此，时间复杂度为O(n²)。请注意，如果使用合并排序或堆排序对各个桶进行排序，则可以降低这种情况下的时间复杂度。

情况	时间复杂度
最佳情况	O(n + k)
平均情况	O(n + k)
最坏情况	O(n²)

空间复杂度

桶排序的空间复杂度为O(n + k)，其中'n'是要排序的输入数组中的元素总数，'k'是桶的总数。这是因为还需要额外的空间来存储桶本身（O(k))，以及将数组元素保存在这些桶内（最坏情况下为 O(n)，如果每个元素都落入特定桶中）。因此，总体空间复杂度是这两者的总和。

空间复杂度	O(n + k)
稳定版	取决于使用的排序算法

桶排序可能是一个稳定的排序算法，也可能不是。因为我们使用插入排序来对存储在桶中的元素进行排序，而插入排序是一种稳定的算法。因此，在本教程中，我们可以说桶排序是一种稳定的算法。如果我们使用一种不稳定的排序算法，那么桶排序也将不稳定。

桶排序的优点

对均匀分布的数据高效：当输入数据在范围内均匀分布时，桶排序效果很好。在这种情况下，桶排序可以实现接近线性的时间复杂度，使其比快速排序或合并排序等其他比较排序更快。

线性时间复杂度（最佳情况）：当数据分布良好时，桶排序可以实现 O(n + k) 的最佳情况时间复杂度，其中 n 是元素数量，k 是桶的数量。这使得桶排序对于特定类型的数据集非常快速。

提供并行化：如果我们观察桶排序的排序性质，我们会发现每个桶都可以独立排序，这有利于并行处理。因此，它可以在拥有多个处理器或内核的系统中提高性能。

易于实现和简单：与快速排序等更复杂的算法相比，桶排序的实现和理解相对简单。这可能是一个巨大的优势，尤其是在开发时间有限的情况下。

可应用于不同的排序算法：为了对桶内的数组元素进行排序，桶排序可以与其他排序算法结合使用，如插入排序或合并排序。因此，桶排序在选择适合特定数据类型的排序方法方面提供了灵活性。

桶排序的缺点

不适合非均匀数据：我们已经看到，如果输入数据分布不均匀，桶排序效果不佳。在这种情况下，一些桶将拥有更多元素，而其他桶可能保持为空。这可能导致工作负载分布不均，进而导致性能下降，使其可能比其他排序算法慢。在最坏的情况下（当所有输入元素都进入特定桶时），桶排序时间复杂度会上升到 O(n²) 时间复杂度。

需要额外空间：在此排序算法中，选择合适的桶数非常重要。过少的桶可能导致元素分布不均和桶内排序缓慢，而过多的桶可能导致空间浪费。

选择桶的排序算法：用于对每个桶内的元素进行排序的算法会影响整体性能。如果为桶排序选择的算法效率较低，则会阻碍整个排序过程。此外，决定选择合适的桶数需要对数据分布有所了解，这在事先确定时可能很麻烦。

仅限于特定数据类型：桶排序对于数值数据类型，特别是浮点数更为有效。桶排序不适用于所有数据类型。

桶创建和管理开销：桶的创建和管理会带来开销，尤其是对于具有大量元素或广泛值范围的数据集。

结论

桶排序主要用于以下两种情况之一。第一种是提高排序过程的速度。将元素放入桶中然后应用排序算法的过程比气泡排序等线性算法快得多。但是，代价是桶排序比线性算法消耗更多的内存。

桶排序选择题

1) 桶排序最有效的情况是 __________。

输入分布不均匀。
输入分布均匀。
输入分布随机。
输入范围很大。

答案： b)

解释：当输入数据在范围内均匀分布时，桶排序效果很好。在这种情况下，桶排序可以实现接近线性的时间复杂度。

2) 桶排序的最坏情况时间复杂度是多少（k 是桶的数量）？

O(n + k)
O(n * k²)
O(n²)
O(n * log(n))

答案：c)

解释：当一个桶接收输入数组的所有元素时，就会发生最坏情况。在这种情况下，插入排序将在数组的所有元素上运行。因此，时间复杂度为 O(n²)。这里，请注意，桶的数量没有起任何重要作用，因为一个桶接收了所有元素。

3) 下列哪一项不会影响桶排序的时间复杂度？

用于对各个桶进行排序的算法实现
使用的桶数
输入分布
输入值

答案： d)

解释：各种因素都会影响桶排序的时间复杂度。这些因素包括用于对各个桶进行排序的算法的实现、使用的桶数以及桶中输入值的分布。它不依赖于输入值。

4) 下列哪一个不一定是一个稳定的排序算法？

合并排序
桶排序
计数排序
无

答案： b)

解释：合并排序和计数排序是稳定的排序算法。然而，桶排序不能保证如此。桶排序的稳定性主要取决于用于对桶中的元素进行排序的排序算法。如果使用的排序算法是稳定的，那么桶排序就是稳定的；否则不是。

5) 下列哪种排序不使用比较排序算法？

冒泡排序
插入排序
选择排序
桶排序

答案： d)

解释：气泡排序、插入排序和选择排序使用比较排序进行排序。桶排序利用元素在桶中的分布来完成排序工作。

下一主题排序算法的时间复杂度

桶排序算法（含Python/Java/C/C++程序）

算法

桶排序的步骤

桶排序算法的工作原理

Python/Java/C/C++/C# 中桶排序的实现

Python 程序

Java 程序

C++ 程序

C 语言程序

C# 程序

复杂度分析

时间复杂度

空间复杂度

桶排序的优点

桶排序的缺点

结论

桶排序选择题

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

桶排序算法（含Python/Java/C/C++程序）

算法

桶排序的步骤

桶排序算法的工作原理

Python/Java/C/C++/C# 中桶排序的实现

Python 程序

Java 程序

C++ 程序

C 语言程序

C# 程序

复杂度分析

时间复杂度

空间复杂度

桶排序的优点

桶排序的缺点

结论

桶排序选择题

相关帖子

希尔排序算法

归并排序算法

插入排序算法

计数排序算法

选择排序算法

堆排序算法

冒泡排序算法

基数排序算法

排序算法的时间复杂度

快速排序算法

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器