希尔排序算法（附带 Python/Java/C/C++ 程序）

2025 年 7 月 7 日 | 阅读 11 分钟

希尔排序是一种原地比较排序算法，由Donald Shell发明。它是插入排序的泛化，通过比较间隔数个位置的元素来克服插入排序的缺点。在插入排序中，元素一次只能向前移动一个位置。它也称为递减增量排序。

希尔排序算法

ShellSort(arr)
    size = length of arr
    gapSize = size / 2
    while gapSize > 0 do
        for j = gapSize to size - 1 do
            temp = arr[j]
            k = j
            while k >= gapSize and arr[k - gapSize] > temp do
                arr[k] = arr[k - gapSize]
                k = k - gapSize
            arr[k] = temp
        gapSize = gapSize / 2 

希尔排序的步骤

步骤 1：将 gapSize（间隔大小）设置为 size / 2，其中 size 是数组的长度。

步骤 2：将给定的数组划分为更小的子部分。每个部分必须与 gapSize 具有相等的间隔。

步骤 3：使用插入排序对这些子列表进行排序。

步骤 4：通过设置 gap = gap / 2 来减小间隔，并重复步骤 2 和 3。

步骤 5：打印排序后的列表。

希尔排序算法的工作原理

现在，让我们看看希尔排序算法的工作原理。为此，我们取一个未排序的数组。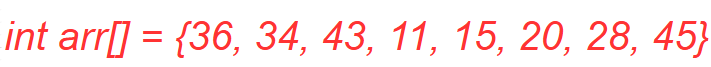

Shell Short Algorithm (With Program in Python/Java/C/C++)

在该数组中，间隔序列为 N/2, N/4, ...., 一直到 1 作为间隔。

在第一个循环中，n 等于 8（数组大小），因此元素位于间隔 4（N/2 = 4）的位置。将比较元素，并在它们未按顺序排列时交换它们。

在这里，在第一个循环中，第 0 个位置的元素将与第 4 个位置的元素进行比较。如果第 0 个元素较大，则会与第 4 个位置的元素交换。否则，它保持不变。这个过程将继续处理剩余的元素。

在间隔为 4 时，子列表为 {36, 15}, {34, 20}, {43, 28}, {11, 45}。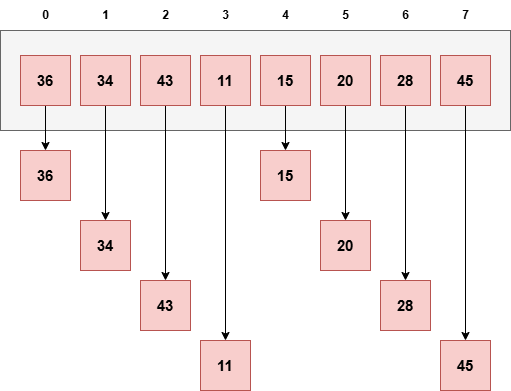

现在，我们必须比较每个子列表中的值。比较后，如果需要在原始数组中进行交换，则进行交换。比较和交换后，更新后的数组将如下所示：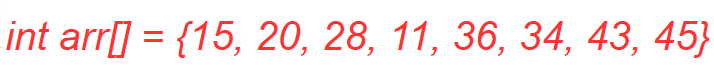

在第二个循环中，元素位于间隔 2（n/4 = 2）的位置，其中 n = 8。

现在，我们取间隔 2 来对数组的其余部分进行排序。间隔为2时，将生成两个子列表：{15, 28, 36, 43} 和 {20, 11, 34, 45}。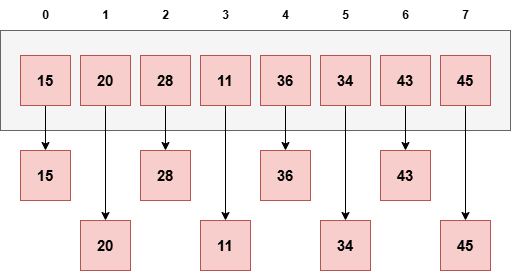

现在，我们必须再次比较每个子列表中的值。比较后，如果需要在原始数组中进行交换，则进行交换。比较和交换后，更新后的数组将如下所示：

在第三个循环中，元素位于间隔 1（n/8 = 1）的位置，其中 n = 8。最后，我们使用值为 1 的间隔来对数组的其余元素进行排序。在此步骤中，希尔排序使用插入排序来对数组元素进行排序。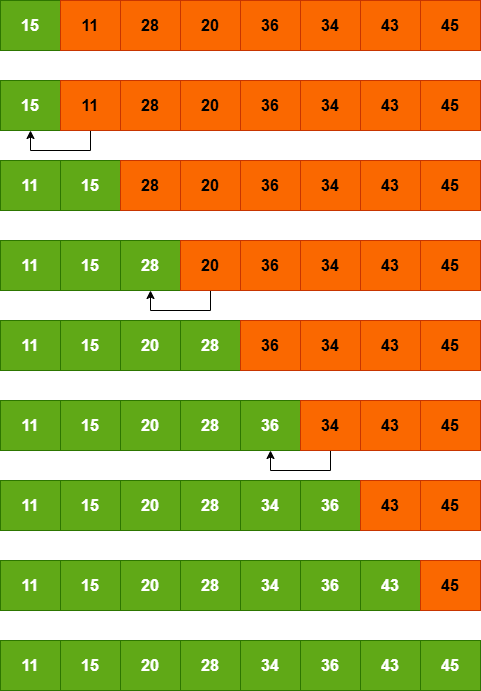

我们可以看到数组最终被排序了。

Python/Java/C/C++/C# 中希尔排序的实现

Python 程序

class ShellSort:
    # A utility function to print an array of size n
    @staticmethod
    def displayArr(inpuptArr):
        for k in inputArr:
            print(k, end=" ")
        print()
    # Function to sort inputArr using Shell Sort
    def sort(self, inpuptArr):
        size = len(inpuptArr)
        # Start with a big gap, then reduce the gap
        gapSize = size // 2
        while gapSize > 0:
            # We are implementing a gapped Insertion Sort with a specified gap size.
            # The first gap elements of the array inputArr [0..gap-1] 
            # are already in the gapped order. Now, we have to keep adding
            # one more element till the complete array is gap-sorted
            # until the entire array is gap-sorted
            for j in range(gapSize, size):
                val = inpuptArr[j]
                k = j
                while k >= gapSize and inpuptArr[k - gapSize] > val:
                    inpuptArr[k] = inpuptArr[k - gapSize]
                    k = k - gapSize
                inpuptArr[k] = val
            gapSize = gapSize // 2
        return 0
# Driver code
if __name__ == "__main__":
    inputArr = [36, 34, 43, 11, 15, 20, 28, 45]
    print("Array before sorting is: ")
    ShellSort.displayArr(inpuptArr)
    obj = ShellSort()
    obj.sort(inpuptArr)
    print("Array after sorting is: ")
    ShellSort.displayArr(inpuptArr)

编译并运行

Java 程序

public class Main {
    // A utility method for printing the elements of the array 
    static void displayArray(int inputArr[]) {
        int size = inputArr.length;
        for (int i=0; i < size; ++i)
            System.out.print(inputArr[i] + " ");
        System.out.println();
    }
    // method for sorting inputArr[] using Shell Sort 
    int sort(int inputArr[]) {
        int size = inputArr.length;
        //We begin with a big gap, then with every 
        // iteration we reduce the gap
        for (int gapSize = size / 2; gapSize > 0; gapSize /= 2) {
            // We are implementing a gapped Insertion Sort with a specified gap size.
            // The first gap elements of the array inputArr[0..gapSize - 1] 
            // are already in the gapped order. Now, we have to keep adding
            // one more element till the complete array is gap-sorted
            // until the entire array is gap-sorted.
            for (int i = gapSize; i < size; i += 1) {
                int val = inputArr[i];
                // shifting in earlier gap-sorted elements till
                //We find the correct position for inputArr[i]
                int k;
                for (k = i; k >= gapSize && inputArr[k - gapSize] > val; k -= gapSize)
                    inputArr[k] = inputArr[k - gapSize];
                // put val (the original a[i]) in its correct
                // location
                inputArr[k] = val;
            }
        }
        return 0;
    }
    // Main method
    public static void main(String args[]) {
        int inputArr[] = {36, 34, 43, 11, 15, 20, 28, 45};
        System.out.println("Array before sorting is: ");
        displayArray(inputArr);
        // creating an object of the Main class
        Main obj = new Main();
        obj.sort(inputArr);
        System.out.println("Array after sorting is: ");
        displayArray(inputArr);
    }
}  

编译并运行

C++ 程序

#include  <iostream>
using namespace std;
// method for sorting inputArr using Shell Sort
int shellSort(int inputArr[], int size){
    // We begin with a big gap. After that, we reduce the size of the gap
    for (int gapSize = size / 2; gapSize > 0; gapSize /= 2){
        // We are implementing a gapped Insertion Sort with a specified gap size.
        // The first gap elements of the array inputArr[0..gap-1] 
        // are already in the gapped order. Now, we have to keep adding
        // one more element till the complete array is gap-sorted
        // until the entire array is gap-sorted.
        for (int i = gapSize; i < size; i += 1)  {
            // We are adding inputArr[i] to the elements that have been gap sorted
            // Saving inputArr[i] in val, and we create a hole at position i
            int val = inputArr[i];
            // Shifting earlier elements that are gap-sorted till the appropriate 
            // location for inputArr[i] is found
            int k;            
            for (k = i; k >= gapSize && inputArr[k - gapSize] > val; k -= gapSize)
                inputArr[k] = inputArr[k - gapSize];
            //  putting val (the original inputArr[i]) at its appropriate location
            inputArr[k] = val;
        }
    }
    return 0;
}
// A utility method for printing the elements of the array
void displayArray(int inputArr[], int size){
    for (int i = 0; i < size; i++)
        cout << inputArr[i] << " ";
}
int main(){
    int inputArr[] = {36, 34, 43, 11, 15, 20, 28, 45};
    int size = sizeof(inputArr)/sizeof(inputArr[0]);
    cout << "Array before sorting is: \n";
    displayArray(inputArr, size);
    shellSort(inputArr, size);
    cout << "\nArray after sorting is: \n";
    displayArray(inputArr, size);
    return 0;
}  

编译并运行

C 语言程序

#include<stdio.h>
// method for sorting inputArr using Shell Sort
int shellSort(int inputArr[], int size){
    // We begin with a big gap. After that, we reduce the size of the gap
    for (int gapSize = size / 2; gapSize > 0; gapSize /= 2) {
        // We are implementing a gapped Insertion Sort with a specified gap size.
        // The first gap elements of the array inputArr[0.. gap - 1] 
        // are already in the gapped order. Now, we have to keep adding
        // one more element till the complete array is gap-sorted
        // until the entire array is gap-sorted.
        for (int i = gapSize; i < size; i += 1)   {
            // We are adding inputArr[i] to the elements that have been gap sorted
            // Saving inputArr[i] in val, and we create a hole at position i
            int val = inputArr[i];
            // Shifting earlier elements that are gap-sorted till the appropriate 
            // location for inputArr[i] is found
            int k;            
            for (k = i; k >= gapSize && inputArr[k - gapSize] > val; k -= gapSize)
                inputArr[k] = inputArr[k - gapSize];
            //  putting val (the original inputArr[i]) at its appropriate location
            inputArr[k] = val;
        }
    }
    return 0;
}
// A utility function for printing the elements of the array
void displayArray(int inputArr[], int size){
    for (int i = 0; i < size; i++) {
        printf("%d", inputArr[i]);
        printf(" ");
    }
}
int main(){
    int inputArr[] = {36, 34, 43, 11, 15, 20, 28, 45};
    int size = sizeof(inputArr)/sizeof(inputArr[0]);
    printf("Array before sorting is: \n");
    displayArray(inputArr, size);
    shellSort(inputArr, size);
    printf("\nArray after sorting is: \n");
    displayArray(inputArr, size);
    return 0;
}  

编译并运行

C# 程序

using System;
class ShellSort {
    // A utility method for printing the elements of the array 
    static void printArray(int []inputArr)  {
        int size = inputArr.Length;
        for (int k = 0; k < size; ++k)
        Console.Write(inputArr[k] + " ");
        Console.WriteLine();
    }
    // method for sorting inputArr using Shell Sort
    int sort(int []inputArr)  {
        int size = inputArr.Length;
        // We begin with a big gap. After that, we reduce the size of the gap
        for (int gapSize = size / 2; gapSize > 0; gapSize /= 2)    {
            // We are implementing a gapped Insertion Sort with a specified gap size.
            // The first gap elements of the array inputArr[0.. gap - 1] 
            // are already in the gapped order. Now, we have to keep adding
            // one more element till the complete array is gap-sorted
            // until the entire array is gap-sorted.
            for (int i = gapSize; i < size; i += 1){
        // We are adding inputArr[i] to the elements that have been gap sorted
                // Saving inputArr[i] in val, and we create a hole at position i
                int val = inputArr[i];
                // Shifting earlier elements that are gap-sorted till the appropriate 
                // location for inputArr[i] is found
                int k;            
                for (k = i; k >= gapSize && inputArr[k - gapSize] > val; k -= gapSize)
                    inputArr[k] = inputArr[k - gapSize];
                // putting val (the original inputArr[i]) at its appropriate location
                inputArr[k] = val;
            }
        }
        return 0;
    }
    // Main method
    public static void Main() {
        int []inputArr = {36, 34, 43, 11, 15, 20, 28, 45};
        Console.Write("Array before sorting is: \n");
        printArray(inputArr);
        // creating an object of the class ShellSort
        ShellSort obj = new ShellSort();
        obj.sort(inputArr);
        Console.Write("Array after sorting is: \n");
        printArray(inputArr);
    }
} 

编译并运行

输出

 
Array before sorting is: 
36 34 43 11 15 20 28 45 
Array after sorting is: 
11 15 20 28 34 36 43 45

复杂度分析

时间复杂度

最佳情况复杂度：当不需要排序时，即数组已排序。希尔排序的最佳情况时间复杂度为 O(n log n)。

平均情况复杂度：当数组元素处于混乱顺序时，既不是完全升序也不是完全降序。希尔排序的平均情况时间复杂度为O(n log n)。

最坏情况复杂度：当数组元素需要按反序排序时发生。也就是说，假设我们要按升序对数组元素进行排序，但其元素是降序的。希尔排序的最坏情况时间复杂度为O(n²)。

情况	时间复杂度
最佳情况	O(n * logn)
平均情况	O(n * logn)
最坏情况	O(n²)

空间复杂度

希尔排序的空间复杂度为O(1)。这是因为希尔排序算法不需要额外的空间进行排序。

另外请注意，希尔排序不是稳定的算法。

希尔排序的应用

希尔排序通常用作插入排序的替代方法，在插入排序需要更长时间来完成给定任务时使用。
当递归超过特定限制时，我们使用希尔排序。
希尔排序对中等大小的数据集效果很好。
希尔排序也用于插入排序以减少操作次数。

希尔排序的优点

比简单排序算法更有效：希尔排序比插入排序和冒泡排序等简单算法更有效，尤其适用于中等大小的数据集。这是因为它允许元素在初始传递中移动更远的距离，从而减少了后期所需的移动次数。
原地排序：希尔排序算法在给定数组内对数据进行排序。因此，对额外内存（O(1) 空间复杂度）的需求最小。因此，希尔排序适用于内存受限的环境。
适应性：希尔排序的性能取决于数据的初始排列方式。当数据接近排序时，它的效果更好，因为它可以快速地将元素放置在其适当的位置。
易于实现：与快速排序或合并排序等更复杂的排序算法相比，希尔排序相对容易实现和理解。

希尔排序的缺点

不稳定：希尔排序不能保证相同值的元素在排序后保留其原始顺序。在需要相等元素的原始顺序的情况下，这可能是一个问题。
依赖于间隔序列：希尔排序使用间隔序列技术来完成排序工作。如果间隔选择不当，则选择的间隔序列可能导致性能下降。
不适合大型数据集：对于非常大的数据集，希尔排序可能比快速排序或合并排序等更高级的算法慢得多。这些算法具有更好的平均和最坏情况时间复杂度。
实现复杂性：尽管希尔排序不像某些其他算法那样复杂，但确定希尔排序的最佳间隔序列需要仔细考虑，在某些情况下可能更繁琐。

结论

总之，希尔排序在易于实现和效率之间取得了很好的平衡。因此，它成为排序任务的宝贵工具，尤其是在处理中等大小的数据集时，其相对于选择排序或冒泡排序等简单算法的优势变得显而易见。

希尔排序算法选择题

1. 谁发明了希尔排序算法？

John Von Neumann
Donald Shell
Tony Hoare
Alan Shell

答案：b)

解释：希尔排序算法由 Donald Shell 发明。

2. 希尔排序的另一个名称是什么？

递减增量排序
递减递减排序
插入排序
选择排序

答案：a)

解释：希尔排序算法也称为递减递减排序。

3. 使用 Shell 的原始增量时的最坏情况时间复杂度是多少？

O(n)
O(n log n)
O(n²)
O(log n)

答案：c)

解释：最坏情况发生在数组元素需要按反序排序时。也就是说，假设我们要按升序对数组元素进行排序，但其元素是降序的。希尔排序的最坏情况时间复杂度为 O(n²)。

4. 哪种排序算法与希尔排序最接近？

合并排序
选择排序
插入排序
桶排序

答案：c)

解释：希尔排序本质上是插入排序的改进版本。它通过允许交换远距离的元素来改进插入排序，从而快速减少大量的混乱。然后，随着间隔的缩小，它以常规插入排序结束——但在更排序的列表中，这使其速度更快。

5. 为什么希尔排序被认为是插入排序的泛化？

它允许交换远距离的元素
它使用递归
它更有效
它使用外部内存

答案：a)

解释：它是插入排序的泛化，它通过比较间隔数个位置的元素来克服插入排序的缺点。在插入排序中，元素一次只能向前移动一个位置。

下一个主题桶排序

希尔排序算法（附带 Python/Java/C/C++ 程序）