堆与树的比较

数据结构在计算机科学中起着重要作用，它促进了数据的组织和操作。树和堆是两种既有相似之处又有独特特征的数据结构。树非常灵活，可以采用各种形状来表示关系和递归结构。

它们常用于文件系统、数据库、编译器和算法中。另一方面，堆是基于树的结构，遵循堆属性，该属性对父节点和子节点的值施加了特定的顺序约束。堆对于实现优先队列尤其有价值，优先队列对于任务调度、数据压缩和图算法（如 Dijkstra 的最短路径算法）至关重要。理解这两种数据结构之间的区别对于开发人员和学生选择合适的结构并提高应用程序的性能至关重要。

什么是堆？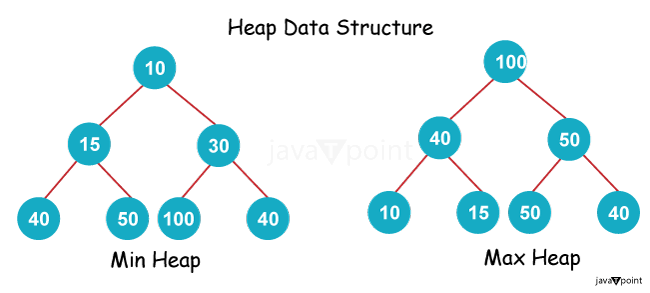

• 堆是一种遵循规则的树状结构；
  
  1. 在最大堆中：每个节点的值都大于或等于其子节点。
  2. 在最小堆中：每个节点的值都小于或等于其子节点。
• 堆的组织方式是树状的，其中：
  
  1. 大多数级别都已完全填充，除了最后一个级别。
  2. 最后一个级别从左到右填充。
  3. 完全二叉树在空间利用方面效率很高，因为所有节点都得到了有效利用。
• 表示
  
  1. 堆通常使用数组来表示。
  2. 对于位置为 i 的节点，其子节点位于位置 2i+1 和 2i+2。
  3. 根节点始终位于位置 0。
• 操作
  
  • 插入：在保持堆属性的同时添加新元素到堆中。
    
    • 新元素被添加到下一个可用位置（数组末尾）。
    • 然后，它会“冒泡向上”，如果违反了堆属性，则与其父节点交换，直到满足堆属性为止。
  • 删除：删除根元素（最大堆中的最大值，最小堆中的最小值）并重构堆。
    
    • 堆中的最后一个元素被移到根位置。
    • 然后它会“冒泡向下”，与其较大的（最大堆）或较小的（最小堆）子节点交换，直到满足堆属性为止。
  • 获取最大/最小值：访问根元素，该元素包含最大值（最大堆）或最小值（最小堆）。
  • 堆化：重构二叉树以满足堆属性，通常在删除后使用。
• 时间复杂度
  
  • 插入：O(log n)
  • 删除：O(log n)
  • 获取最大/最小值：O(1)
  • 堆化：O(log n)
• 应用
  
  • 高效实现优先队列。
  • 用于图算法，如 Dijkstra 的最短路径。
  • 堆排序算法。
  • 操作系统中的作业调度。
  • 事件驱动仿真和数值计算。

堆结构提供了一种有效维护部分排序数据结构的方法，使其适用于优先队列实现以及需要频繁访问最大或最小元素的算法。

输出

什么是树？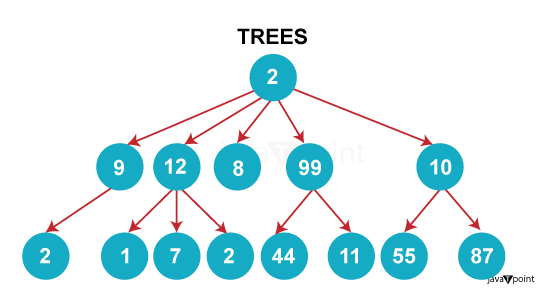

树是一种线性的分层数据结构，其中节点通过边相互连接。

关键要素

• 节点：节点是树的一个单元，它包含数据并指向其子节点。
• 根节点：根节点是树层级结构中没有父节点的节点。
• 父节点：具有一个或多个子节点的节点。
• 子节点：连接到父节点的节点。
• 叶节点：没有任何子节点的节点称为叶节点或外部节点。
• 内部节点：具有至少一个子节点的节点。
• 边：父节点与其子节点之间的链接。

特性

1. 树中的每个节点（根节点除外）都有一个父连接。
2. 节点可以有子节点。
3. 树中的每个节点都有从根节点开始的一条路径。
4. 树遵循一种模式，其中每个子节点成为其子树的根。

树的类型

• 二叉树：每个节点最多可以有两个子节点的树，称为左子节点和右子节点。
• 二叉搜索树：一棵二叉树，其中每个节点的值都大于其左子树中的所有值，并且小于其右子树中的所有值。
• 平衡树：一棵树，其中任何节点的两个子树的高度最多相差一。例如 AVL 树和红黑树。
• N叉树：每个节点最多可以有 N 个子节点的树，其中 N 是一个固定的正整数。

遍历算法

• 深度优先遍历：在回溯之前，沿着每个分支尽可能深地探索来遍历树。
  
  • 前序遍历。根 -> 左子树 -> 右子树
  • 中序遍历。左子树 -> 根 -> 右子树（用于二叉搜索树）
  • 后序遍历。左子树 -> 右子树 -> 根
• 广度优先遍历（层序遍历）：逐层遍历树，在移动到下一层之前访问当前层的所有节点。

应用程序的不同使用方式

• 文件系统：以一种结构化的方式组织文件和文件夹。
• 数据库索引：提高数据搜索和检索效率。
• 编译器：分析编程语言语法和解析。
• 人工智能：实现决策树、游戏树和搜索树。
• 网络：利用路由和生成树算法进行通信。
• 数据压缩：使用霍夫曼编码和前缀树来存储数据。

输出

堆与树的比较；

结构

• 树的每个父节点可以有任意数量的子节点，从而创建具有不同深度和宽度的结构。树中的值不需要遵循顺序约束。
• 堆是二叉树的一种形式，其中每个节点最多可以有两个子节点。它们遵循堆属性，该属性强制对父节点和子节点的值施加顺序约束（最大堆或最小堆）。

形状

• 树的形状可能不同，根据插入顺序和特定的树实现，从倾斜树到完全树不等。
• 堆始终保持树状结构，这意味着所有级别都已填充，除了最后一个级别可能需要从左到右填充。这种形状属性在插入和删除过程中保持一致。

值顺序；

• 通常，树不强制父节点或子节点与其值之间的顺序约束。
• 在最大堆中，每个父节点的值都大于或等于其子节点。在最小堆中，每个父节点的值都小于或等于其子节点。

起点；

• 在树结构中，根节点不一定与其他节点有任何显着性或连接性。
• 在最大堆中，根节点包含整个堆中的最大值。在最小堆中，根节点包含整个堆中的最小值。

操作

• 树的常见操作包括插入、删除、搜索和遍历（前序、中序、后序、层序）。
• 堆的常见操作包括插入、删除和访问最大/最小值（根节点）。这些操作具有高效的时间复杂度（插入和删除为 O(log n)，访问最大/最小值为 O(1)）。

应用；

• 树用于表示各种应用程序中的分层数据结构，例如文件系统、数据库索引、编译器、决策树、游戏树和搜索树。
• 堆经常用于实现优先队列，用于任务调度、数据压缩算法和图算法（如 Dijkstra 的最短路径算法）等任务。

时间复杂度；

• 树操作的时间复杂度可能因树的结构和实现而有很大差异。例如，平衡树的插入和删除复杂度可能为 O(log n)。倾斜树的复杂度可能为 O(n)。
• 由于其二叉树结构，堆具有保证的时间复杂度；插入和删除操作为 O(log n)，访问最大/最小值 O(1)。

虽然堆和树都用作数据结构，但堆专门用于高效地维护排序结构和快速访问极端值。树在表示具有不同形状和结构的关系方面提供了灵活性，而没有特定的顺序约束。在权衡堆或树时，这完全取决于问题的需求 - 例如，如果您需要快速的优先队列操作，您处理的数据类型以及您希望不同操作运行的速度。

以下是树和堆之间的表格差异