前序遍历

在本文中，我们将讨论数据结构中的前序遍历。像栈、数组、队列等线性数据结构只有一种遍历数据的方式。但在像树这样的层次化数据结构中，有多种遍历数据的方式。

在前序遍历中，首先访问根节点，然后是左子树，之后再访问右子树。前序遍历的过程可以表示为 -

在前序遍历中，根节点总是最先被遍历，而在后序遍历中，根节点是最后一个被遍历的项。前序遍历用于获取树的前缀表达式。

执行前序遍历的步骤如下 -

• 首先，访问根节点。
• 然后，访问左子树。
• 最后，访问右子树。

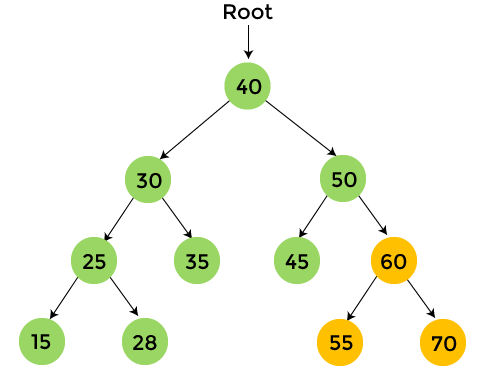
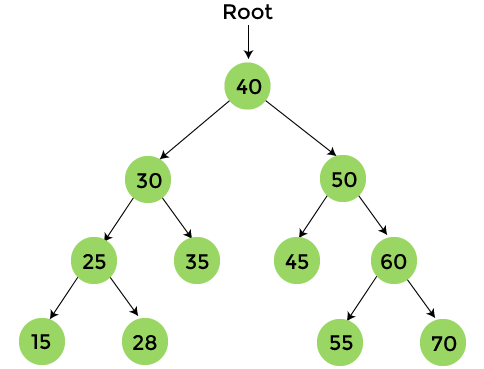
前序遍历技术遵循根-左-右的策略。前序（Preorder）这个名字本身就表明根节点会首先被遍历。

算法

现在，让我们看看前序遍历的算法。

前序遍历示例

现在，我们来看一个前序遍历的例子。通过一个例子，理解前序遍历的过程会更容易。

黄色节点是尚未访问的节点。现在，我们将使用前序遍历来遍历上图树中的节点。

• 从根节点 40 开始。首先，打印 40，然后递归遍历左子树。
  
• 现在，移动到左子树。对于左子树，根节点是 30。打印 30，然后移动到 30 的左子树。
  
• 在 30 的左子树中，有一个元素 25，所以打印 25，然后遍历 25 的左子树。
  
• 在 25 的左子树中，有一个元素 15，且 15 没有子树。所以，打印 15，然后移动到 25 的右子树。
  
• 在 25 的右子树中，有 28，且 28 没有子树。所以，打印 28，然后移动到 30 的右子树。
  
• 在 30 的右子树中，有 35，它没有子树。所以打印 35，然后遍历 40 的右子树。
  
• 在 40 的右子树中，有 50。打印 50，然后遍历 50 的左子树。
  
• 在 50 的左子树中，有 45，它没有任何子节点。所以，打印 45，然后遍历 50 的右子树。
  
• 在 50 的右子树中，有 60。打印 60，然后遍历 60 的左子树。
  
• 在 60 的左子树中，有 55，它没有任何子节点。所以，打印 55，然后移动到 60 的右子树。
  
• 在 60 的右子树中，有 70，它没有任何子节点。所以，打印 70 并停止该过程。
  

完成前序遍历后，最终输出为 -

40, 30, 25, 15, 28, 35, 50, 45, 60, 55, 70

前序遍历的复杂度

前序遍历的时间复杂度是 O(n)，其中 'n' 是二叉树的大小。

而前序遍历的空间复杂度是 O(1)，如果我们不考虑函数调用的栈大小。否则，前序遍历的空间复杂度是 O(h)，其中 'h' 是树的高度。

前序遍历的实现

现在，让我们看看在不同编程语言中前序遍历的实现。

程序：编写一个程序，用 C 语言实现前序遍历。

输出

执行上述代码后，输出将是 -

程序：编写一个程序，用 C++ 实现前序遍历。

输出

执行上述代码后，输出将是 -

程序：编写一个程序，用 C# 实现前序遍历。

输出

执行上述代码后，输出将是 -

程序：编写一个程序，用 Java 实现前序遍历。

输出

执行上述代码后，输出将是 -

所以，这就是关于本文的全部内容。希望本文能对您有所帮助并提供信息。