伸展树

Splay Tree 是一种自平衡或自适应的二叉搜索树。换句话说，我们可以说 Splay Tree 是二叉搜索树的变体。Splay Tree 的先决条件是我们应该了解二叉搜索树。

正如我们已经知道的，二叉搜索树在各种情况下的时间复杂度。二叉搜索树在平均情况下的时间复杂度是 O(logn)，在最坏情况下的时间复杂度是 O(n)。在二叉搜索树中，左子树的值小于根节点，右子树的值大于根节点；在这种情况下，时间复杂度为 O(logn)。如果二叉树是左倾斜或右倾斜的，则时间复杂度为 O(n)。为了限制倾斜，AVL 和 Red-Black tree 出现了，在所有情况下，所有操作的时间复杂度都为 O(logn)。我们还可以通过进行更多实际实现来改进此时间复杂度，因此设计了一种新的树 数据结构，称为 Splay tree。

什么是 Splay Tree？

Splay tree 是一种自平衡树，但 AVL 和 Red-Black trees 也是自平衡树。是什么使 Splay tree 与这两种树不同？它有一个额外的属性使其独特，那就是 splaying（伸展）。

Splay tree 包含与 二叉搜索树 相同的操作，即插入、删除和搜索，但它还包含一个额外的操作，即 splaying。因此，Splay tree 中的所有操作之后都会进行 splaying。

Splay tree 不是严格平衡树，而是大致平衡的树。让我们来理解 Splay tree 中的搜索操作。

假设我们要搜索图中所示的 7 这个元素。

要搜索 Splay tree 中的任何元素，首先，我们将执行标准的二叉搜索树操作。由于 7 小于 10，我们将移到根节点的左侧。执行搜索操作后，我们需要执行 splaying。这里的 splaying 意味着我们对任何元素执行的操作，在执行一些重排后，该元素应该成为根节点。树的重排将通过旋转来完成。

注意：Splay tree 可以定义为自适应树，其中对元素执行的任何操作都会重排树，使执行操作的元素成为树的根节点。

旋转

用于 splaying 的旋转有六种类型

1. Zig 旋转（右旋转）
2. Zag 旋转（左旋转）
3. Zig zag（先 Zig 后 Zag）
4. Zag zig（先 Zag 后 Zig）
5. Zig zig（两次右旋转）
6. Zag zag（两次左旋转）

选择旋转类型的所需因素

以下是用于选择旋转类型的因素

• 我们要旋转的节点是否有祖父节点？
• 该节点是父节点的左子节点还是右子节点？
• 该节点是祖父节点的左子节点还是右子节点？

旋转情况

情况 1：如果节点没有祖父节点，并且它是父节点的右子节点，则执行左旋转；否则，执行右旋转。

情况 2：如果节点有祖父节点，则根据以下场景执行旋转：

场景 1：如果节点是父节点的右子节点，并且父节点也是其父节点的右子节点，则执行 zig zig 右右旋转。

场景 2：如果节点是父节点的左子节点，但父节点是其父节点的右子节点，则执行 zig zag 右左旋转。

场景 3：如果节点是父节点的右子节点，并且父节点是其父节点的右子节点，则执行 zig zig 左右旋转。

场景 4：如果节点是父节点的右子节点，但父节点是其父节点的左子节点，则执行 zig zag 右左旋转。

现在，让我们通过示例来理解上述旋转。

为了重排树，我们需要执行一些旋转。Splay tree 中的旋转类型如下：

• Zig 旋转

当要搜索的项是根节点或根节点的子节点（即左子节点或右子节点）时，使用 Zig 旋转。

在 Splay tree 中搜索时可能出现的场景如下：

情况 1：如果搜索项是树的根节点。

情况 2：如果搜索项是根节点的子节点，则会出现两种场景：

1. 如果子节点是左子节点，则执行右旋转，称为 zig 右旋转。
2. 如果子节点是右子节点，则执行左旋转，称为 zig 左旋转。

让我们通过一个示例来看上面的两种场景。

考虑下面的示例

在上面的例子中，我们要搜索树中的 7 这个元素。我们将遵循以下步骤：

步骤 1：首先，我们将 7 与根节点进行比较。由于 7 小于 10，所以它是根节点的左子节点。

步骤 2：找到元素后，我们将执行 splaying。执行右旋转，使 7 成为树的根节点，如下所示：

让我们看另一个例子。

在上面的例子中，我们要搜索树中的 20 这个元素。我们将遵循以下步骤：

步骤 1：首先，我们将 20 与根节点进行比较。由于 20 大于根节点，所以它是根节点的右子节点。

步骤 2：找到元素后，我们将执行 splaying。执行左旋转，使 20 元素成为树的根节点。

• Zig zig 旋转

有时会出现这种情况，即要搜索的项同时具有父节点和祖父节点。在这种情况下，我们需要执行四次旋转来进行 splaying。

让我们通过一个示例来理解这种情况。

假设我们要搜索下面树中的 1 这个元素。

步骤 1：首先，我们要执行标准的 BST 搜索操作以搜索 1 这个元素。由于 1 小于 10 和 7，所以它会在节点 7 的左侧。因此，元素 1 拥有一个父节点，即 7，以及一个祖父节点，即 10。

步骤 2：在此步骤中，我们需要执行 splaying。我们需要借助一些旋转使节点 1 成为根节点。在这种情况下，我们不能简单地执行 zig 或 zag 旋转；我们必须实现 zig zig 旋转。

为了使节点 1 成为根节点，我们需要执行两次右旋转，称为 zig zig 旋转。当我们执行右旋转时，10 将向下移动，节点 7 将向上移动，如下面的图所示：

再次，我们将执行 zig 右旋转，节点 7 将向下移动，节点 1 将向上移动，如下所示：

正如我们在上面的图中观察到的，节点 1 已成为树的根节点；因此，搜索已完成。

假设我们要搜索下面树中的 20。

为了搜索 20，我们需要执行两次左旋转。以下是搜索 20 节点所需的步骤：

步骤 1：首先，我们执行标准的 BST 搜索操作。由于 20 大于 10 和 15，所以它会在节点 15 的右侧。

步骤 2：第二步是执行 splaying。在这种情况下，将执行两次左旋转。在第一次旋转中，节点 10 将向下移动，节点 15 将向上移动，如下所示：

在第二次左旋转中，节点 15 将向下移动，节点 20 成为树的根节点，如下所示：

正如我们所观察到的，执行了两次左旋转；因此，它被称为 zig zig 左旋转。

• Zig zag 旋转

到目前为止，我们已经了解到父节点和祖父节点要么是 RR 关系，要么是 LL 关系。现在，我们将看到父节点和祖父节点之间的 RL 或 LR 关系。

让我们通过一个示例来理解这种情况。

假设我们要搜索下面树中的 13 这个元素。

步骤 1：首先，我们执行标准的 BST 搜索操作。由于 13 大于 10 但小于 15，所以节点 13 将是节点 15 的左子节点。

步骤 2：由于节点 13 在 15 的左侧，而节点 15 在节点 10 的右侧，因此存在 RL 关系。首先，我们对节点 15 执行右旋转，15 将向下移动，13 将向上移动，如下所示：

仍然，节点 13 不是根节点，并且 13 在根节点的右侧，所以我们将执行左旋转，称为 zag 旋转。节点 10 将向下移动，13 成为根节点，如下所示：

正如我们在上面的树中观察到的，节点 13 已成为根节点；因此，搜索已完成。在这种情况下，我们首先执行了 zig 旋转，然后执行了 zag 旋转；因此，它被称为 zig zag 旋转。

• Zag zig 旋转

让我们通过一个示例来理解这种情况。

假设我们要搜索下面树中的 9 这个元素。

步骤 1：首先，我们执行标准的 BST 搜索操作。由于 9 小于 10 但大于 7，所以它将是节点 7 的右子节点。

步骤 2：由于节点 9 在节点 7 的右侧，而节点 7 在节点 10 的左侧，因此存在 LR 关系。首先，我们对节点 7 执行左旋转。节点 7 将向下移动，节点 9 向上移动，如下所示：

节点 9 仍然不是根节点，并且 9 在根节点的左侧，所以我们将执行右旋转，称为 zig 旋转。执行右旋转后，节点 9 成为根节点，如下所示：

正如我们可以观察到的，节点 13 是根节点；因此，搜索已完成。在这种情况下，我们首先执行了 zag 旋转（左旋转），然后执行了 zig 旋转（右旋转），因此它被称为 zag zig 旋转。

Splay tree 的优点

• 在 Splay tree 中，我们不需要存储额外的信息。相比之下，在 AVL 树中，我们需要存储每个节点的平衡因子，这需要额外的空间，而 Red-Black trees 也需要存储一个额外的位信息来表示节点的颜色，即红色或黑色。
• 它是各种实际应用中最快的二叉搜索树类型。它用于 Windows NT 和 GCC 编译器。
• 它提供了更好的性能，因为经常访问的节点会移近根节点，从而可以在 Splay trees 中快速访问元素。它用于缓存实现，因为最近访问的数据存储在缓存中，这样我们就无需访问内存来获取数据，从而节省了时间。

Splay tree 的缺点

Splay tree 的主要缺点是树不是严格平衡的，即它们大致平衡。有时 Splay trees 是线性的，因此它将需要 O(n) 的时间复杂度。

Splay tree 中的插入操作

在插入操作中，我们首先将元素插入树中，然后对插入的元素执行 splaying 操作。

15, 10, 17, 7

步骤 1：首先，我们将节点 15 插入树中。插入后，我们需要执行 splaying。由于 15 是根节点，所以我们不需要执行 splaying。

步骤 2：下一个元素是 10。由于 10 小于 15，所以节点 10 将是节点 15 的左子节点，如下所示：

现在，我们执行splaying。为了使 10 成为根节点，我们将执行右旋转，如下所示：

步骤 3：下一个元素是 17。由于 17 大于 10 和 15，所以它将成为节点 15 的右子节点。

现在，我们将执行 splaying。由于 17 具有父节点和祖父节点，所以我们将执行 zig zig 旋转。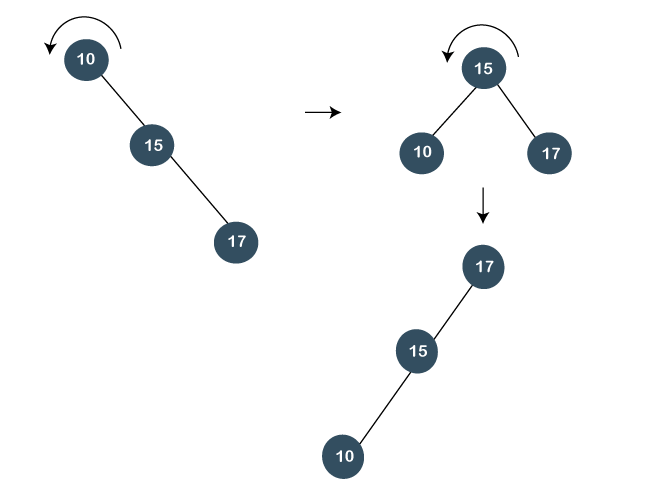

在上面的图中，我们可以观察到 17 已成为树的根节点；因此，插入已完成。

步骤 4：下一个元素是 7。由于 7 小于 17、15 和 10，所以节点 7 将是 10 的左子节点。

现在，我们需要 splay 树。由于 7 具有父节点和祖父节点，所以我们将执行两次右旋转，如下所示：

节点 7 仍然不是根节点，它是根节点 17 的左子节点。所以，我们需要对根节点执行一次右旋转，即 17，使节点 7 成为根节点，如下所示：

插入操作的算法

在上面的算法中，T 是树，n 是我们要插入的节点。我们创建了一个临时变量，其中包含根节点的地址。我们将运行 while 循环，直到 temp 的值变为 NULL。

插入完成后，将执行 splaying。

Splaying 操作的算法

在上面的实现中，x 是执行旋转的节点，而 y 是节点 x 的左子节点。

left.rotation(T, x) 的实现

在上面的实现中，x 是执行旋转的节点，而 y 是节点 x 的右子节点。

Splay tree 中的删除

我们知道 Splay trees 是二叉搜索树的变体，所以 Splay tree 中的删除操作将与 BST 类似，但唯一的区别是 Splay trees 中的删除操作之后会进行 splaying 操作。

删除类型

Splay tree 中有两种删除类型：

1. 自底向上 splaying
2. 自顶向下 splaying

自底向上 splaying

在自底向上 splaying 中，我们首先从树中删除元素，然后对删除的节点执行 splaying。

让我们通过示例来理解 Splay tree 中的删除。

假设我们要从下面显示的树中删除 12 和 14。

• 首先，我们简单地执行标准的 BST 删除操作来删除 12 这个元素。由于 12 是叶节点，所以我们只需从树中删除该节点。

删除尚未完成。我们需要 splay 被删除节点的父节点，即 10。我们必须在树上执行 Splay(10)。正如我们在上面的树中观察到的，10 在节点 7 的右侧，而节点 7 在节点 13 的左侧。所以，首先，我们对节点 7 执行左旋转，然后我们对节点 13 执行右旋转，如下所示：

节点 10 仍然不是根节点；节点 10 是根节点的左子节点。所以，我们需要对根节点（即 14）执行右旋转，以使节点 10 成为根节点，如下所示：

• 现在，我们必须从树中删除 14 这个元素，如下所示：

我们知道我们不能简单地删除内部节点。我们将使用中序前驱或中序后继来替换节点的值。假设我们使用中序后继，其中我们将值替换为右子树中存在的最小值。节点 14 的右子树中的最小值是 15，所以我们将 14 的值替换为 15。由于节点 14 成为叶节点，所以我们可以像下面这样简单地删除它：

删除尚未完成。我们需要执行另一个操作，即 splaying，我们需要将删除节点的父节点设为根节点。删除之前，节点 14 的父节点是根节点，即 10，所以我们不需要在这种情况下执行任何 splaying。

自顶向下 splaying

在自顶向下 splaying 中，我们首先对要执行删除的节点执行 splaying，然后从树中删除节点。一旦元素被删除，我们将执行 join 操作。

让我们通过一个示例来理解自顶向下 splaying。

假设我们要删除下面树中的 16。

步骤 1：在自顶向下 splaying 中，我们首先对节点 16 执行 splaying。节点 16 同时具有父节点和祖父节点。节点 16 在其父节点的右侧，并且父节点在其父节点的右侧，所以这是一个 zag zag 情况。在这种情况下，首先，我们将对节点 13 执行左旋转，然后是 14，如下所示：

节点 16 仍然不是根节点，并且它是根节点的右子节点，所以我们需要对节点 12 执行左旋转，以使节点 16 成为根节点。

一旦节点 16 成为根节点，我们将删除节点 16，并且我们将得到两个不同的树，即左子树和右子树，如下所示：

我们知道左子树的值总是小于右子树的值。左子树的根是 12，右子树的根是 17。第一步是找到左子树中的最大元素。在左子树中，最大元素是 15，然后我们需要对 15 执行 splaying 操作。

正如我们在上面的树中观察到的，元素 15 具有父节点和祖父节点。一个节点在其父节点的右侧，并且父节点在其父节点的右侧，所以我们需要执行两次左旋转才能使节点 15 成为根节点，如下所示：

在对树执行两次旋转后，节点 15 成为根节点。正如我们所看到的，15 的右子节点是 NULL，所以我们将 17 附加到 15 的右侧，如下所示，这个操作被称为join操作。

注意：如果要删除的元素不存在于 Splay tree 中，则将执行 splaying。Splaying 将在到达 NULL 之前对最后访问的元素执行。

Delete 操作的算法

在上面的算法中，我们首先检查根是否为 Null；如果根为 NULL，则表示树为空。如果树不为空，我们将对要删除的元素执行 splaying 操作。一旦 splaying 操作完成，我们将比较根数据与要删除的元素；如果两者不相等，则表示元素不存在于树中。如果相等，则可能出现以下情况：

情况 1：根的左边是 NULL，根的右边成为根节点。

情况 2：如果左边和右边都存在，那么我们 splay 左子树中的最大元素。当 splaying 完成后，最大元素成为左子树的根。右子树将成为左子树根节点的右子节点。