数据结构中的雨水收集问题

引言

如果你注意到两侧（左侧和右侧）有更高的障碍物，那么数组中的一个组件可以蓄水。两侧障碍物的高度可用于确定每个位置需要储存多少水。

每个索引所包含的总水量是液体所包含的总量。在立式高度图上，每个单独障碍物的尺寸为 1。计算地形映射障碍物的高度，正整数和小数可以表示这些高度，以获得下雨时可以储存的水量。

示例

输入

输出

8

让我们检查上面案例的推理

下面提供了一张地形图，以象征上面提到的高度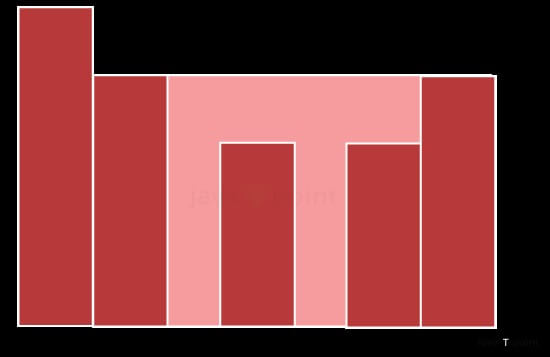

其中

第一个块可以容纳三个单位的雨水。

第二个空间块可以容纳一个单位的水。

第三个结构可以容纳三个单位的水。

第四个块可以容纳一个单位的水。

因此，容器内水占据的面积等于

解决雨水收集挑战的基本概念是，只有当当前块的左右两侧都存在更高高度的块时，雨水才能以单个单位的形式被储存。

因此，雨水被困在当前块的最高点。因此，很明显，在流动块的左右两侧可以找到的最大和最小高度，减去块的整体高度，决定了可能被困住的液体体积。

解决雨水收集问题有五种方法；这些方法如下所述。

1. 暴力法
2. 前缀和后缀数组
3. 使用堆
4. 水平扫描系统
5. 使用双指针

方法 1 (暴力法)

遍历数组的每个成员，以识别数组两侧最大的障碍物。

选择两个高度中较短的一个。此数组组件可以容纳的水量等于其当前最大高度与其减小高度之间的区别。为了将此概念付诸实践，请采取以下步骤：从头到尾遍历数组

关于每个组件：从这个索引开始，探索值数组以获得尽可能高的最大高度 (a)，并通过从当前索引到最终位置遍历集合来获得最大高度 (b)。添加此数字以确定已保存的总水量。这些列中将保存的液体总量是 min(a,b) - array[i]。保存总水量。

下面提供了收集雨水的第一个方法——暴力法。我们需要为数组中的每个组件（即块）获取左右两侧的最高高度，因此遍历数组 [] 中的每个元素。对于每个组件（即块），找到左侧的最高点和另一侧的最高点。在当前块中，添加 min(right_max_height, left_max_height) - Arr[i] 作为结果（捕获的流体）。

此方法的算法步骤如下所示

• 创建一个名为 res 的变量并将其起点设置为 0。
• 对于每个值，从 1 到 n 遍历数组 Arr[]
• 在启动时，将 max_left 和 max_right 都设置为 0。
• 将 Arr[i] 移动到集合的开头以修改左侧最大值
• max_left = max(Arr[i], max_left)
• 以相同的方式修改右侧最大值，将 A[i] 移动到结果数组的最后一段。right_maximum = max(Arr[i], max_right)
• 将 Arr[i] - min(left_maximum, max_right) 纳入 res。

使用暴力法实现

//使用暴力法实现雨水收集的 Python 代码

输出

上述代码的输出是

说明

该程序确定了可能被一系列不同高度的房屋捕获的降水量。它通过从可能被限制在每个建筑物表面的最大水量中减去建筑物的高度来实现这些。

程序代码最初将每个建筑物左侧和右侧可能被限制的最大水高度分别存储在名为 left_max 和 right_max 的数组中。通过从左到右重复遍历数组并记录迄今为止可见的最大数字，填充 left_max 数组。

right_max 数组通过从右到左重复遍历数组并记录迄今为止可见的天顶来填充。一旦 left_max 和 right_max 数组填充完毕，该定律再次遍历数组。对于每个结构，它通过取该结构的 left_max 和 right_max 值中的最小值并减去结构本身的高度来计算可能被捕获的水量。

被困水的典型体积也一再积累。下面是一个说明该定律如何适用于数组 (4, 3, 0, 2, 0, 2, 3) 的例子。

left_max 数组填充了值 (4, 4, 4, 4, 4, 4)。

right_max 数组填充了值 (3, 3, 3, 3, 2, 2)。

该定律遍历数组并计算每个结构可能被捕获的水量。

• 对于构建 0，可能被捕获的水量为 min(4, 3) - 0 = 3。
• 对于构建 1，可能被捕获的水量为 min(4, 3) - 3 = 0。
• 对于结构 2，可能被捕获的水量为 min(4, 3) - 0 = 3。
• 对于构建 3，可能被捕获的水量为 min(4, 3) - 2 = 1。
• 对于构建 4，可能被捕获的水量为 min(3, 2) - 0 = 2。
• 对于构建 5，可能被捕获的水量为 min(3, 2) - 2 = 0。
• 对于构建 6，可能被捕获的水量为 min(2, 2) - 3 = -1（但我们不能有负水，所以我们将其设置为零）。
• 因此，可能被捕获的总水量为 3+0+3+1+2+0+0 = 9。

时间复杂度

O (n^2)，因为每个值都覆盖了左右两侧。

空间复杂度

O (1)，因为在执行此方法时没有使用新的空间。

方法 2 (前缀和后缀数组或预计算)

下面给出了使用前缀和后缀数组的另一种雨水收集方法。现在，我们将效率从 O(N^2) 提高到 O(N)。请记住，在使用暴力法时，我们为每个元素都覆盖了左侧和右侧。但是，如果我们存储这些数据，我们可以通过一次遍历来解决问题，从而有效地将时间复杂度降低到 O(N)。

建议假设两个数组，左侧最大值和右侧最大值，其中左侧最大值 (i) 将存储直到指示器左侧的最高点。类似地，右侧最大值 (i) 将跟踪直到指示器 i 右侧的最大高度。

算法

• 生成两个数组，即右侧最大值和左侧最大值，大小相同。
• 生成一个变量 m = 0。
• 继续从左到右覆盖，更新 mix = maximum(mix, Arr(i))，并将左侧外部 = mix 设置为每个指示器。类似地，从 N 到 1 剪切一个圆并更新 mxi = maximum(mxi, Arr(i)) 并为每个指示器分配右侧外部 = mxi。
• 将变量的初始值设置为 0，然后从 0 到 N-1 遍历。将 min(left_outside(i), right_outside(i)) - Arr(i) 添加到每个指示器。
• 这是基于预计算概念的有效结果。
• 在以前的方法中，对于每个元素，我们需要计算左侧和右侧的最高元素。
• 因此，为了降低时间复杂度。
• 对于每个元素，我们可以预先计算并存储左侧和右侧的最高条（例如，存储在数组 left() 和 right() 中）。
• 此外，重复数组并使用预先计算的值来查找此指示器中存储的水量。这与 (min(left(i), right(i)) - arr(i)) 相同。
• 请参阅下面的示例以更好地理解。
• 图解

考虑 arr() = { 3, 0, 2, 0, 4}

因此，left() = { 3, 3, 3, 3, 4}，right() = { 4, 4, 4, 4, 4}。

现在考虑使用 i 从 0 到末尾重复。

对于 i = 0，

> left(0, 0) = 3，right(0, 0) = 4，arr(0, 0) = 3。

=> 储存的水量 = min(left_wing(0), right_wing(0)) - arr(0) = min(3, 4) - 3 = 3 - 3 = 0

=> 总计 = 0 + 0 = 0

对于 i = 1，

=> left(1) = 3，right(1) = 4，arr(1) = 0。

=> 储存的水量 = min(left_wing(1), right(1)) - arr(1) = min(3, 4) - 0 = 3 - 0 = 3

=> 总计 = 0 + 3 = 3

对于 i = 2，

=> left(2) = 3，right(2) = 4，arr(2) = 2。

=> 储存的水量 = min(left_wing(2), right_wing(2)) - arr(2) = min(3, 4) - 2 = 3 - 2 = 1

=> 总计 = 3 + 1 = 4

对于 i = 3，

=> left(3) = 3，right(3) = 4，arr(3) = 0。

=> 储存的水量 = min(left_wing(3), right_wing(3)) - arr(3) = min(3, 4) - 0 = 3 - 0 = 3

=> 总计 = 4 + 3 = 7

对于 i = 4，

=> left(4) = 4，right(4) = 4，arr(4) = 4。

=> 储存的水量 = min(left_wing(4), right_wing(4)) - arr(4) = min(4, 4) - 4 = 4 - 4 = 0

=> 总计 = 7 + 0 = 7

因此，捕获的总雨水量 = 7

请按照以下步骤应用此方法。

生成大小为 N 的两个数组（left() 和 right()）。生成一个变量（例如，maximum）来存储遍历过程中直到某个指示器的外部设置。

从开始到结束运行一个循环。

在每次复制中，更新最大值并分配 left(i) = max。

从结束到开始运行另一个循环。

在每次复制更新中，设置到目前为止的最大设置并分配 right(i) = max。

从开始到结束遍历数组。

该列中将存储的水量为 min(left(i), right(i)) - array(i)。

将此值添加到存储的水总量中。

发布存储的水总量。

Python 中该方法的实现

输出

说明

该定律计算了可能被一系列以高度数组表示的房屋捕获的雨水量。它通过找到每个结构两侧可能被捕获的水的高度，并减去结构本身的高度来实现这一点。

该定律首先初始化数组 left_max 和 right_max，以分别保持每个结构左侧和右侧可能被捕获的最大水高度。left_max 数组是通过从左到右重复遍历数组并记录迄今为止可见的最大顶部来填充的。right_max 数组是通过从右到左重复遍历数组并记录迄今为止可见的天顶来填充的。

一旦 left_max 和 right_max 数组被填充，该定律再次遍历数组。对于每个构造，它通过取该构造的 left_max 和 right_max 值中的最小值并减去构造本身的高度来计算可能被捕获的水量。捕获水的标准量子也从下部反向收集。

接着是一个关于定律如何作用于数组 (0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1) 的例子。

left-max 数组填充了值 (0, 1, 1, 2, 2, 2, 3, 3)。

rightmax 数组填充了值 (3, 3, 3, 3, 2, 2, 2, 2, 1, 1, 1)。

该定律遍历数组并计算每个构造中可能被捕获的水量。

• 对于结构 0，可能被捕获的水量是 min(0, 3) - 0 = 3。
• 对于构造 1，可能被捕获的水量是 min(1, 3) - 1 = 0。
• 对于构造 2，可能被捕获的水量是 min(1, 3) - 0 = 1。
• 对于结构 3，可能被捕获的水量是 min(2, 3) - 2 = 0。
• 对于结构 4，可能被捕获的水量是 min(2, 2) - 1 = 1。
• 对于构造 5，可能被捕获的水量是 min(2, 2) - 0 = 2。
• 对于构造 6，可能被捕获的水量是 min(2, 2) - 1 = 1。
• 对于结构 7，可能被捕获的水量是 min(3, 2) - 1 = 1。
• 对于结构 8，可能被捕获的水量是 min(3, 1) - 2 = 0。
• 对于结构 9，可能被捕获的水量是 min(3, 1) - 1 = 0。
• 对于构造 10，可能被捕获的水量是 min(3, 1) - 2 = 0。
• 对于结构 11，可能被捕获的水量是 min(3, 1) - 1 = 0。
• 因此，可能被捕获的水的总量是 0+0+1+0+1+2+1+1+0+0+0+0 = 6。

该定律的时间复杂度为 O(n)，其中 n 是输入数组的长度。这是因为该定律在三种情况下遍历数组：一次填充 left_max 数组，一次填充 right_max 数组，以及一次计算每个结构中可能被捕获的水量。

该定律的空间复杂度为 O(n)，其中 n 是输入数组的长度。这是因为该定律使用了两个数组，left_max 和 right_max，每个数组的大小都为 n。

方法 3（使用堆栈）

使用堆栈解决问题的思路如下

我们可以使用一个堆栈来跟踪由高级左右条形图限制的条形图。这只需一次复制即可完成。

为此，我们将不断将元素推入堆栈，直到找到一个值比堆栈顶部更高的元素。这表示当前元素左侧有可能存储位置，当前条形图是末端。

因此，移除左侧较低的元素并找到左侧条形图（即堆栈的当前顶部）和左侧末端条形图存储的水量，当前条形图是右侧末端。继续此操作，直到堆栈不为空或找到更高值的元素。

请参阅下面的示例以更好地理解。

算法

考虑数组 arr() = { 3, 0, 2, 0, 4} 和一个空堆栈。

对于 i = 0，

堆栈是空的。所以，没有元素，左侧的值更高。

=> 将指示器推入堆栈。st = { 0}（用于跟踪两者之间的距离）

对于 i = 1，

=> arr(1) 小于 arr(stack top)。因此 arr(1) 具有更高的左翼边界。

=> 将指示器推入堆栈。st = { 0, 1}

对于 i = 2，

=> arr(2) 小于 arr(stack top)。因此 arr(2) 是当前堆栈顶部的更高右边界。

=> 计算堆栈顶部左右边界之间储存的水量。

堆栈顶部是左右边界之间的基础高度。

=> 弹出堆栈顶部。因此 st = { 0}。

=> 当 arr(0) 和 arr(2) 是边界时，之间储存的水量 = { min(arr(0), arr(2)) - arr(1)} * (2 - 0 - 1) = 2。

=> arr(0) 小于 arr(2)。将指示器推入堆栈。st = { 0, 2}。

=> 储存的总水量 = 0 + 2 = 2。

对于 i = 3，

=> arr(3) 小于 arr(2)。因此 Arr(3) 具有更高的左翼边界。

=> 将指示器推入堆栈。st = { 0, 2, 3}。

对于 i = 4，

=> arr(4) 小于 arr(stack top)。因此 arr(4) 是当前堆栈顶部的更高右边界。

=> 以与 i = 2 相同的方式计算储存的水量。基础高度为 ~3。

=> 弹出堆栈顶部。因此 st = { 0, 2}。

=> 当 arr(4) 和 arr(2) 是边界时，之间储存的水量 = { min(arr(4), arr(2)) - arr(3)} * (4 - 2 - 1) = 2。

=> arr(4) 小于 arr(2)。

=> 弹出堆栈。st = { 0}。

=> 储存的水量在 arr(0) 和 arr(4) 之间

当 arr(2) 是基础高度时 = { min(3, 4) - 2} * (4 - 0 - 1) = 3

=> arr(0) 小于 arr(4)。因此弹出堆栈。st = {}。

由于堆栈中没有元素，将指示器推入。st = { 4}。

=> 储存的总水量 = 2 + 2 + 3 = 7。

因此，储存的水总量为 7。

请按照以下步骤应用该想法。

遍历条形数组的指标。

对于每个条形图，执行以下操作：

循环，直到堆栈不为空且当前条形图的高度小于堆栈的顶部条形图。

将顶部条形图的指示器存储在 pop_height 中，并将其从堆栈中弹出。

找到弹出条形图的左侧条形图（当前顶部）与当前条形图之间的距离。

找到顶部条形图和当前条形图之间的最小高度。

可以捕获的最大水量是距离 * min_height。

捕获的水量，包括弹出的条形图，是 (距离 * min_height) 减去 (pop_height)。

将其添加到答案中。

返回输入的量子作为水的总量子。

实施

输出

说明

该定律定义了一个名为 maximum_Water 的特征，该特征以表示条形高度的整数表作为输入。

该特征初始化一个空堆栈 stack 和一个变量 maximum_water，用于存储可能存储的最大水量。

该函数遍历高度表中的每个条形图。

当堆栈不为空且当前条形图高于堆栈顶部的条形图时，特定操作执行以下操作。

弹出堆栈顶部的条形图。

计算弹出条形图的左右条形图之间的空间。

计算左右条形图之间的最小顶部。

将一些条形图捕获的水域面积添加到 maximum_water 中。

该特征将当代条形图的指示器推入堆栈。

最终，该特征返回 maximum_water。

简单来说，该定律通过寻找可以在它们之间显示水的条形高度来发挥作用。每个条形图的左侧和右侧的条形图都应该比最大条形图更高，以便捕获水。可以捕获的水量等于两个条形图之间的最小峰值乘以它们之间的距离。

该定律使用一个堆栈来跟踪迄今为止可见的条形图。堆栈被异常地弹出，确实，当一个条形图被设置时。这比堆栈顶部的条形图更高。这是因为任何低于堆栈下方条形图的条形图都不能用超现代高度条形图诱捕任何水。

方法 4（垂直检查系统）

思路如下

如果 max_height 是最高块的高度，那么它将是任何被困雨水可能达到的最大高度。

如果对于每个单位的高度，我们找到该高度的左翼和最右侧边界，我们可以考虑所有中间的块都包含该水量子。

但这也会考虑条形图的高度。因此，我们必须从被困水的总量中减去它。

这可以这样解释：假设某个高度的段是 {i1, i2}, {i2, i3}, ..., {ik-1, ik}。

因此，单个高度单位之间存储的水量是指标之间的差值。

= (i2 - i1 - 1)(i3 - i2 - 1)...(ik - ik-1 - 1}) = ik - i1 - (k - 1)，其中 k 是中间条形图的数量。

但是由于我们考虑了左右边界之间的所有块，它也考虑了所有条形图。

因此，单个单位的被困水变为 (ik - i1)。

请参阅下面的示例以更好地理解。

图解

考虑数组 arr() = { 3, 0, 2, 0, 4}。

= 4，所有块的总和为 2 + 3 + 4 = 9。

对于高度 = 1，

> 最左边界 = 0，最右边界 = 4。

所有中间的块都包含 1 米的水。

=> 因此，捕获的水量 = (4 - 0) = 5

=> 捕获的总水量 = 0 + 5 = 5

对于高度 = 2

> 最左边界 = 0，最右边界 = 4。

> 所有中间的块都包含两个高度的水。

> 之前，我们考虑了高度为 1 的水柱。因此，高度增加了 1 个单位。

=> 因此，捕获的水量 = (4 - 0) = 5

=> 捕获的总水量 = 5 + 5 = 10

对于高度 = 3，

> 最左边界 = 0，最右边界 = 4。

> 所有中间的块都包含三个高度的水。

之前，我们考虑了高度为 2 的水柱。因此，高度增加了 1 个单位。

=> 因此，捕获的水量 = (4 - 0) = 5

=> 捕获的总水量 = 10 + 5 = 15

对于高度 = 4

> 最左边界 = 4，最右边界 = 4。

所有中间的块都包含 4 米的水。

之前，我们考虑了高度为 3 的水柱。因此，高度增加了 1 个单位。

=> 因此，捕获的水量 = (4 - 4 + 1) = 1

=> 捕获的总水量 = 15 + 1 = 16

因此，捕获的总水量 = 16 减去条形图占据的总空间 = 16 减去 9 = 7。

请按照以下步骤应用该想法。

找到块的总数，即 heights 数组的总和，num_blocks。

找到最大高度。

将总水量存储在一个变量中，aggregate = 0。

保留两个指针，left = 0 和 right = N-1，以存储每个高度单位的左翼和最右侧边界。

对于从 1 到 max_height 的每个高度，执行以下操作：

找到当前高度的左翼和最右侧边界。

如前所述，我们可以认为这些中间的所有块至少包含一个单位的水。

将此水量添加到捕获的总水量中。

复制完成后，从总量中减去 num_blocks，因为在计算过程中我们已将它们视为水高。

实施

上述方法的实现如下

输出

说明

Python 代码实现“水平扫描”技术，以确定在由一组高程区域表示的全景图中，块之间捕获了多少水

1. 任务定义

函数 `Water_trapped(array)` 接收一个表示块高度的行数组，并返回这些块中捕获的水的总量。

2. 背景

初始化变量，如 `number_of_blocks`、`size`、`size` 和 `maximum_height`。- `number_of_blocks` 记录块的总范围（最高范围之和）；`size` 存储数组的持续时间；`maximum_height` 存储块的最大高度。

3. 在更高层次上重复。

该属性迭代从 1 到 `maximum_height` 的每个可能的顶点。

4. 可用性扫描

对于每个高度 `i`，它从左到右垂直扫描，并相应地向左扫描，以找到两侧的高度大于或等于 `i` 的左侧和右侧。- 这是通过 while 循环递增或递减左右指令 (`left_array` 和 `right_array`) 来完成的，直到引用具有最高最大值或等于 `i` 的块。

5. 捕获水计算

对于每个 `i`，计算该层中捕获的流，由于 `right_array` 和 `left_array` 之间的差异，加上 1（表示当前块）。- 这适用于所有水体。

6. 最终计数

通过迭代所有高程，该功能从计算的总捕水量中移除块的总数，并仅将块从计算中排除。

7. 结果正在发布

最终，质量返回整个阵列中最重的水。

方法 5（使用双指针）

生成两个指针，一个在数组的左侧，一个在数组的右侧。但是，如果左侧有一个块，则捕获的水的总量将取决于从右到左和从左到右的方向。

算法

生成并设置 left_pointer = 0, right_pointer = n-1, ans = 0。

生成两个变量 left_maximum 和 right_maximum，并将它们设置为 0。

当 left_pointer <= right_pointer 时，继续覆盖数组并

如果 Arr(left_pointer) < Arr(right_pointer) 且 left_maximum > Arr(left_maximum)，

将 left_maximum - Arr(left_pointer) 添加到 ans

如果 left_maximum < Arr(left_pointer)

将 left_maximum 更新为 Arr(left_pointer)。

将左指针增加 1

以类似的方式，如果 Arr(left_pointer) > Arr(right_pointer) 且 Arr(right_maximum) > Arr(right_pointer)，

将 right_maximum - Arr(right_maximum) 添加到 ans

如果 right_maximum < Arr(right_maximum)

将 right_maximum 更新为 Arr(right_pointer)。

将指针增加 1。

发布文章。

实施

输出

结论

双指针方法效果最好，因为它具有 O(N) 的时间复杂度和 O(1) 的空间复杂度。

最高块的高度将决定任何被困雨水可能达到的最大高度。

被困水的总量是通过从总和的最大高度中减去块数来计算的。