广度优先搜索 (BFS) 算法

在本文中，我们将讨论数据结构中的 BFS 算法。广度优先搜索是一种图遍历算法，它从根节点开始遍历图，并探索所有相邻节点。然后，它选择最近的节点并探索所有未探索的节点。在使用 BFS 进行遍历时，图中的任何节点都可以被视为根节点。

遍历图的方法有很多种，但其中 BFS 是最常用的方法。它是一种递归算法，用于搜索树或图数据结构的所有顶点。BFS 将图的每个顶点分为两类 - 已访问和未访问。它选择图中的一个节点，然后访问与所选节点相邻的所有节点。

BFS 算法的应用

广度优先算法的应用如下：

• BFS 可用于从给定源位置查找相邻位置。
• 在对等网络中，BFS 算法可以用作遍历方法来查找所有相邻节点。大多数洪流客户端，例如 BitTorrent、uTorrent 等，都采用此过程来查找网络中的“种子”和“对等点”。
• BFS 可用于网络爬虫以创建网页索引。它是可用于索引网页的主要算法之一。它从源页面开始遍历并遵循与该页面相关的链接。在这里，每个网页都被视为图中的一个节点。
• BFS 用于确定最短路径和最小生成树。
• BFS 也用于 Cheney 技术来复制垃圾回收。
• 它可用于 Ford-Fulkerson 方法，以计算流网络中的最大流量。

算法

BFS 算法探索图的步骤如下：

步骤 1： 将 G 中每个节点的 STATUS 设置为 1（就绪状态）

步骤 2： 将起始节点 A 入队并将其 STATUS 设置为 2（等待状态）

步骤 3： 重复步骤 4 和 5，直到 QUEUE 为空

步骤 4： 将节点 N 出队。处理它并将其 STATUS 设置为 3（已处理状态）。

步骤 5： 将 N 的所有处于就绪状态（其 STATUS = 1）的邻居入队并设置

它们的 STATUS = 2

（等待状态）

[循环结束]

步骤 6： 退出

BFS 算法示例

现在，让我们通过一个示例来了解 BFS 算法的工作原理。在下面的示例中，有一个具有 7 个顶点的有向图。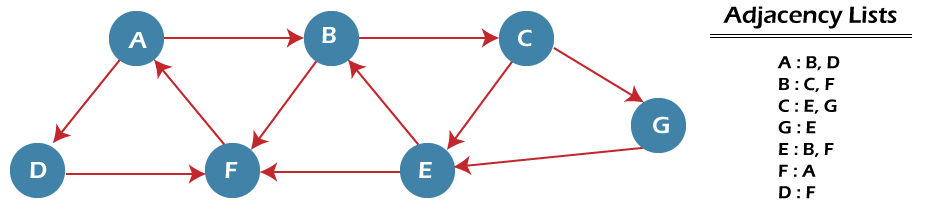

在上面的图中，可以使用 BFS 找到最短路径“P”，它将从节点 A 开始到节点 E 结束。该算法使用两个队列，即 QUEUE1 和 QUEUE2。QUEUE1 包含所有要处理的节点，而 QUEUE2 包含所有已处理并从 QUEUE1 中删除的节点。

现在，让我们从节点 A 开始检查图。

步骤 1 - 首先，将 A 添加到 queue1，将 NULL 添加到 queue2。

步骤 2 - 现在，从 queue1 中删除节点 A 并将其添加到 queue2。将节点 A 的所有邻居插入 queue1。

步骤 3 - 现在，从 queue1 中删除节点 B 并将其添加到 queue2。将节点 B 的所有邻居插入 queue1。

步骤 4 - 现在，从 queue1 中删除节点 D 并将其添加到 queue2。将节点 D 的所有邻居插入 queue1。节点 D 的唯一邻居是 F，因为它已插入，所以不会再次插入。

步骤 5 - 从 queue1 中删除节点 C 并将其添加到 queue2。将节点 C 的所有邻居插入 queue1。

步骤 5 - 从 queue1 中删除节点 F 并将其添加到 queue2。将节点 F 的所有邻居插入 queue1。由于节点 F 的所有邻居都已存在，我们将不会再次插入它们。

步骤 6 - 从 queue1 中删除节点 E。由于它的所有邻居都已添加，所以我们不会再次插入它们。现在，所有节点都已访问，并且目标节点 E 出现在 queue2 中。

BFS 算法的复杂度

BFS 的时间复杂度取决于用于表示图的数据结构。BFS 算法的时间复杂度为 O(V+E)，因为在最坏的情况下，BFS 算法会遍历每个节点和每条边。在图中，顶点数为 O(V)，而边数为 O(E)。

BFS 的空间复杂度可以表示为 O(V)，其中 V 是顶点的数量。

BFS 算法的实现

现在，让我们看看 BFS 算法在 Java 中的实现。

在此代码中，我们使用邻接列表来表示我们的图。在 Java 中实现广度优先搜索算法使得处理邻接列表变得容易得多，因为我们只需要在节点从队列头部（或开始）出队后，遍历连接到每个节点的节点列表一次。

在此示例中，我们用于演示代码的图如下：

输出

结论

在本文中，我们讨论了广度优先搜索技术及其示例、复杂度和在 Java 编程语言中的实现。在这里，我们还看到了 BFS 的实际应用，这表明它是一个重要的数据结构算法。

那么，关于这篇文章就到这里。希望它能对您有所帮助和启发。

BFS 算法的 MCQ 练习

问题 1： 以下哪项准确描述了 BFS 算法的初始步骤？

1. 将起始节点入队并将其状态设置为已处理。
2. 将起始节点入队并将其状态设置为等待。
3. 将起始节点入队并将其状态设置为就绪。
4. 将起始节点出队并将其状态设置为等待。

问题 2： BFS 通常被优先用于在无权重图中寻找最短路径的主要原因是什么？

1. BFS 总是以深度优先的方式探索节点。
2. BFS 保证首先探索最浅的节点。
3. BFS 使用优先级队列来寻找最短路径。
4. 在所有情况下，BFS 都比 DFS 快。

问题 3： 在 BFS 的上下文中，“已处理状态”表示什么？

1. 节点已准备好入队。
2. 节点已出队，其所有邻居都已入队。
3. 节点当前正在探索中。
4. 节点已被标记为已访问但尚未处理。

问题 4： 布尔数组“nodes”在 BFS 的 Java 实现中扮演什么角色？

1. 跟踪队列中当前节点。
2. 存储从起始节点到最短距离。
3. 记录节点是否已被访问。
4. 存储每个节点的父节点。

问题 5： 关于 BFS 算法的时间复杂度，哪个说法是正确的？

1. 时间复杂度为 O(V)，因为 BFS 只遍历每个顶点一次。
2. 时间复杂度为 O(E)，因为 BFS 只遍历每条边一次。
3. 时间复杂度为 O(V^2)，因为嵌套循环。
4. 时间复杂度为 O(V + E)，因为 BFS 只遍历每个顶点和每条边一次。