第 k1 小和第 k2 小元素之间的元素之和

我们需要找到给定向量中第 k1 小和第 k2 小元素之间的元素总和。

用户提供两个索引和输入向量。

让我们通过一个例子来理解。

如果向量是 [ 1 4 2 6 8 11 10] 并且 k1, k2 为 2,5。

在这里，我们必须找到 k1 和 k2 索引之间的数字总和。

但首先，我们需要对给定的向量进行排序，然后对从 k1 到 k2 索引的值求和。

因此，排序后，向量变成如下：

[1 2 4 6 8 10 11].

如果我们从 0 开始考虑索引，则从索引 2 到索引 5 的值的总和为 4+6+8+10 = 28。

现在我们需要实现一个代码来找到 k1 和 k2 索引之间的值之和，包括 k1 和 k2 索引。

代码

输出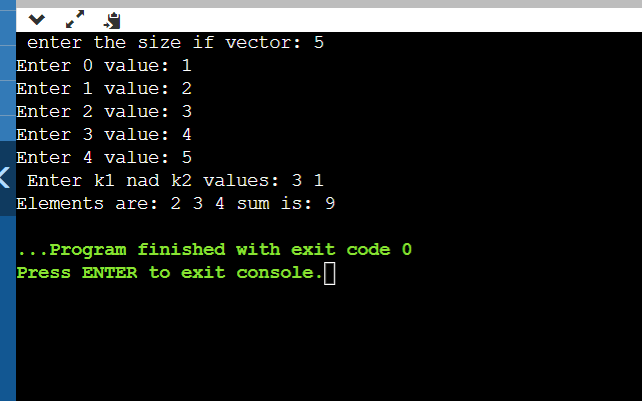

说明

首先，我们包含了执行代码所需的库。

代码的这部分将以输入的形式获取向量元素，并存储在名为 vec 的向量中。

接下来，我们需要对向量进行排序，以便轻松遍历其中最小的元素。

上面的代码行将对给定的输入向量进行排序，其中 sort 是一个内置函数，它接受向量的开始和结束地址作为参数。

接下来，我们需要提示用户输入 k1 和 k2 索引，以查找 k1 和 k2 索引之间的元素总和。

这部分代码将处理 ka 和 k2 值的输入，如果 k2<k1，我们还会交换 k1 和 k2，因为如果 k2<k1，我们将无法通过循环迭代。

所以，我们交换了两个元素。

接下来，我们需要计算从索引 k1 到索引 k2 的总和，我们还将打印构成该总和的值。

上面的循环计算从 k1 到 k2 索引之间的元素总和，包括 k1 和 k2 索引。

它还将打印构成总和的元素。

最后，我们将打印从索引 k1 到 k2 的值的总和。

我们还将处理用户给出的 k1 或 k2 值大于或等于 n 的情况。在这种情况下，我们无法计算总和，因为我们会遇到一个错误，称为向量索引越界，即我们正在尝试访问向量中不存在的元素。

下面的代码负责处理这些情况。

处理这种情况的输出是：

时间和空间复杂度

时间复杂度：对向量进行排序以计算总和的时间复杂度为 O(N*log(N))，在最坏情况下为 O(N)。

总时间复杂度为 O(N)+O(N*log(N))。

空间复杂度：如果不考虑输入的空间，则代码占用恒定空间。