快速排序算法 (附 Python/Java/C/C++ 程序)

2025 年 5 月 7 日 | 阅读 12 分钟

快速排序是一种利用分治技术的排序算法。它选择一个基准元素，并将其放在已排序数组的适当位置。

分治法是一种将算法分解为子问题，然后解决子问题，并将结果组合起来以解决原始问题的方法。

分治：首先，选择一个基准元素。然后，将数组分区或重新排列成两个子数组，使得左子数组中的每个元素都小于或等于基准元素，右子数组中的每个元素都大于基准元素。
解决：使用快速排序递归地对两个子数组进行排序。
合并：合并已排序的数组。

步骤：

步骤 1：选择基准元素。通常选择第一个、最后一个或中位数元素作为基准元素。

步骤 2：对数组进行分区。为此，请围绕基准元素重新排列数组的元素。分区后，基准元素左侧的元素（左子数组）小于基准元素，基准元素右侧的元素（右子数组）大于基准元素。

步骤 3：对左子数组和右子数组重复上述步骤。这可以通过递归完成。当子数组只剩下一个元素时，递归停止。因为单个元素已经是排序好的。

算法

function quickSort(arr, low, high):
    if low < high:
        pivotIndex = partition(arr, low, high)
        quickSort(arr, low, pivotIndex - 1)  // Sort left half
        quickSort(arr, pivotIndex + 1, high) // Sort right half
function partition(arr, low, high):
    pivot = arr[high]  // Choose the last element as the pivot
    i = low - 1        // Pointer for greater element
    for j from low to high - 1:
        if arr[j] ≤ pivot:
            i = i + 1
            swap(arr[i], arr[j])
    swap(arr[i + 1], arr[high])  // Move pivot to its correct position
    return i + 1

快速排序算法的工作原理

实现快速排序的简单步骤如下。

步骤 1：选择基准元素。通常选择第一个、最后一个或中位数元素作为基准元素。在本例中，我们选择最后一个元素作为基准。此外，取两个指针 j 和 k，其中 j 的值为 -1，k 指向数组的第 0 个索引。移动 j 指针，使得 j 指针指向的元素及其左侧的元素都小于基准元素。

步骤 2：将 a[k]，即 19，与基准元素进行比较。我们看到 a[k] > 基准元素。因此，将 k 增加 1。现在，k 指向第 1 个索引。

步骤 3：将 a[k]，即 4，与基准元素进行比较。我们看到 a[k] < 基准元素。因此，将 j 增加 1。现在，j 指向第 0 个索引。

步骤 4：交换 a[j] 和 a[k]，并将 k 增加 1。现在，k 指向第 2 个索引。

步骤 5：将 a[k]，即 13，与基准元素进行比较。我们看到 a[k] < 基准元素。因此，将 j 增加 1。现在，j 指向第 1 个索引。

步骤 6：交换 a[j] 和 a[k]，并将 k 增加 1。现在，k 指向第 3 个索引。

步骤 7：将 a[k]，即 18，与基准元素进行比较。我们看到 a[k] > 基准元素。因此，将 k 增加 1。现在，k 指向第 4 个索引。

步骤 8：将 a[k]，即 10，与基准元素进行比较。我们看到 a[k] < 基准元素。因此，将 j 增加 1。现在，j 指向第 2 个索引。

步骤 9：交换 a[j] 和 a[k]，并将 k 增加 1。现在，k 指向第 5 个索引。

步骤 10：将 a[k]，即 10，与基准元素进行比较。我们看到 a[k] < 基准元素。因此，将 j 增加 1。现在，j 指向第 3 个索引。

步骤 11：交换 a[j] 和 a[k]，并将 k 增加 1。现在，k 指向第 6 个索引。

步骤 12：将 a[k]，即 15，与基准元素进行比较。我们看到 a[k] < 基准元素。因此，将 j 增加 1。现在，j 指向第 4 个索引。

步骤 13：交换 a[j] 和 a[k]。由于 k 指向最后一个元素，因此进一步的检查和交换停止在此处。请注意，j 索引左侧的所有元素以及 j 索引处的元素都小于基准元素。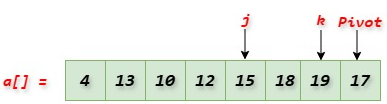

步骤 14：将 a[j + 1] 与基准元素交换（交换 18 和 17）。

我们看到基准元素已放置在排序数组的正确位置。

步骤 15：根据基准元素将数组划分为左子数组和右子数组。位于基准元素左侧的元素是左子数组的一部分，位于基准元素右侧的元素是右子数组的一部分。

步骤 16：对左子数组和右子数组重复所有步骤。

Python/Java/C/C++/C# 中的快速排序实现

Python 程序

# Partition function
def partition(a, l, h):
    # pick the pivot
    pvt = a[h]
    # j is the index of the elements that are smaller than  
    # pivot element. It also indicates the right position of the pivot found so far
    j = l - 1
    # Traverse a[l..h] and move all smaller
    # elements to the left side. Elements from l to 
    # j is smaller after every iteration
    for k in range(l, h):
        if a[k] < pvt:
            j += 1
            swap(a, j, k)
    # Move pivot after smaller elements and
    # return its position
    swap(a, j + 1, h)
    return j + 1
# Swap function
def swap(a, j, k):
    a[j], a[k] = a[k], a[j]
# The QuickSort function implementation
def qckSort(a, l, h):
    if l < h:
        # pi is the partition return index of pivot
        pi = partition(a, l, h)
        # Recursion calls for smaller elements
        # and greater than or equal to elements
        qckSort(a, l, pi - 1)
        qckSort(a, pi + 1, h)
# Main driver code
if __name__ == "__main__":
    a = [10, 7, 8, 9, 1, 5]
    size = len(a)
    print("The array before sorting is: ")
    for v in a:
        print(v, end=" ")
    print()  
    qckSort(a, 0, size - 1)
    print("The array after sorting is: ")
    for v in a:
       print(v, end=" ")

立即执行

Java 程序

public class Main {
          // Partition method
         static int partitionArray (int[] a, int l, int h) {
        // Choose the pvt
        int pvt = a[h];
        // The index j decides the position of the pivot. 
        int j = l - 1;
        // Traverse all the elements from l to h-1 
        // and shift all the smaller elements to the left side of the array
        // elements. From low to j are the elements that are lesser than the
        // pivot element. Therefore, the elements that are larger than the pivot
        // automatically takes the right side of the array.		
        for (int k = l; k <= h - 1; k++) {
            if (a[k] < pvt) {
           // lesser element found, so 
	// increase j by 1
                j = j + 1;
                swapEle(a, j, k);
            }
        }
        // Move the pivot to its appropriate position
        swapEle(a, j + 1, h); 
        // return the position of the pivot, that will
        //helps to partition the array into two halves.		
        return j + 1;
    }
    // Swap method for swapping elements located
    // at index j and index k in the array
    static void swapEle(int[] a, int j, int k) {
        int tmp = a[j];
        a[j] = a[k];
        a[k] = tmp;
    }
    // Implementation of the QuickSort method
    static void quickSort(int[] a, int l, int h) {
         // base case: when the number of elements in the array
         // is only one, the array is already sorted.
        if (l < h) {
            // pIndex is the partition return index of the pivot element in the sorted array
            int pIndex = partitionArry(a, l, h);
            // Recursive calls for the elements that are smaller than the pivot element
            quickSort(a, l, pIndex - 1);
	// Recursive calls for the elements that are greater than or equal to the pivot element
            quickSort(a, pIndex + 1, h);
        }
    }
    // main method
    public static void main(String[] args) {
        int[] a = {10, 7, 8, 9, 1, 5};
        int n = a.length;
        System.out.println("The array before sorting is: ");
        for (int k = 0; k < n; k++) {
            System.out.print(a[k] + " ");  
        }
        quickSort(a, 0, n - 1);
        System.out.println();
        System.out.println("The array after sorting is: ");
        for (int k = 0; k < n; k++) {
            System.out.print(a[k] + " ");  
        }
    }
}

编译并运行

C++ 程序

#include <bits/stdc++.h>
using namespace std;
int partition(vector<int>& arr, int low, int high) {
    // Choose the pivot
    int pivot = arr[high];
    // Index of smaller element and indicates 
    //The right position of the pivot found so far
    int i = low - 1;
    // Traverse arr[low..high] and move all smaller
    // elements on the left side. Elements from low to 
    // i are smaller after every iteration
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(arr[i], arr[j]);
        }
    }
    // Move pivot after smaller elements and
    // return its position
    swap(arr[i + 1], arr[high]);  
    return i + 1;
}
// The QuickSort function implementation
void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        // pi is the partition return index of pivot
        int pi = partition(arr, low, high);
        // Recursion calls for smaller elements
        // and greater than or equal to elements
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}
int main() {
    vector<int> arr = {10, 7, 8, 9, 1, 5};
    int n = arr.size();
    cout<<"The array before sorting is: \n";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout<<endl;
    quickSort(arr, 0, n - 1);
    cout<<"The array after sorting is: \n";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    return 0;
}

编译并运行

C 语言程序

#include <stdio.h>
// function used for swapping elements
void swapEle(int *e, int *g) {
  int s = *e;
  *e = *g;
  *g = s;
}
// function that returns the position of the partition 
int partition(int a[], int l, int h) {
  // picking the rightmost element as the pivot element
  int pvt = a[h];
  // pointer for larger element
  int j = (l - 1);
  // traversing each element of the array
  // and comparing them with the pivot element
  for (int k = l; k < h; k++) {
    if (a[k] <= pvt) {
      // If the element is less than the pivot is found
      // Swap it with the larger element pointed by j
      j = j + 1;
      // swapping element at j with the element at k
      swapEle(&a[j], &a[k]);
    }
  }
  // Swapping the pivot element 
  // with the larger element located at j + 1
  swapEle(&a[j + 1], &a[h]);
  // return the point of partition 
  return (j + 1);
}
void qckSort(int a[], int l, int h) {
  if (l < h) {
    // finding the pivot element in such a way that
    // elements less than the pivot element are on the left of the pivot
    // elements larger than the pivot element are on the right of the pivot
    int p = partition(a, l, h);
    // recursive call on the left of the pivot
    qckSort(a, l, p - 1);
    // recursive call on the right of pivot
    qckSort(a, p + 1, h);
  }
}
// function to print array elements
void displayArray(int a[], int s) {
  for (int j = 0; j < s; ++j) {
    printf("%d ", a[j]);
  }
  printf("\n");
}
// main function
int main() {
  int a[] = {10, 7, 8, 9, 1, 5};
  int s = sizeof(a) / sizeof(a[0]);
  printf("The array before sorting is: \n");
  displayArray(a, s);
  // perform quicksort on the array
  qckSort(a, 0, s - 1);
  printf("The array after sorting is: \n");
  displayArray(a, s);
}

编译并运行

C# 程序

using System;
class QuickSort {
    // function for doing the Partition
    static int Partition(int[] a, int l, int h) {
        //The last element is chosen as the pivot
        int pvt = a[h];
        // Index of the lesser element and indicates 
        //The appropriate position of the pivot found so far
        int j = l - 1;
        // Traversing a[l..h] and move all the elements 
     // that are than the pivot on the left side.
        // Elements from l to j are smaller after every iteration
        for (int k = l; k <= h - 1; k++) {
            if (a[k] < pvt) {
                j = j + 1;
                SwapEle(a, j, k);
            }
        }
        // shifting the pivot after the lesser elements and
        // returning its index
        SwapEle(a, j + 1, h);  
        return j + 1;
    }
    // function for swapping element located at j and k index
    static void SwapEle(int[] a, int j, int k) {
        int t = a[j];
        a[j] = a[k];
        a[k] = t;
    }
    // Implementating the QuickSort function 
    static void QckSort(int[] a, int l, int h) {
        if (l < h) {
            // p contains the location index where pivot is located
            int p = Partition(a, l, h);
            // Recursive calls for lesser elements
            // and larger or equals elements
            QckSort(a, l, p - 1);
            QckSort(a, p + 1, h);
        }
    }
    static void Main(string[] args) {
        int[] a = {10, 7, 8, 9, 1, 5};
        int s = a.Length;
		Console.Write("The array before sorting is: \n");
		foreach (int val in a) {
            Console.Write(val + " "); 
        }
        Console.Write("\n");
        QckSort(a, 0, s - 1);
        Console.Write("The array after sorting is: \n");
        foreach (int val in a) {
            Console.Write(val + " "); 
        }
    }
}

编译并运行

复杂度分析

场景	时间复杂度
最佳情况	(Ω(n log n)：最佳情况发生在基准元素将数组分成两半时。
平均情况	(θ(n log n))：平均而言，基准元素将数组分成两部分，但不一定是相等的部分。
最坏情况	(O(n²)) 发生的情况是，当选择最大元素或最小元素作为已排序数组的基准元素时。

空间复杂度：空间复杂度为 **O(n)**，因为递归调用堆栈，其中 n 是输入数组中元素的总数。

快速排序的应用

许多政府和私营部门实体使用商业计算来组织不同类型的数据，例如按名称/日期/价格排列文件、按学号对学生进行排序以及按指定 ID 组织账户配置文件，因为它是处理大型数据集最快的通用算法。
在不需要稳定排序的地方，可以使用快速排序。要实现稳定性，可以使用归并排序。
在编程语言的库函数中，快速排序用于对数组进行排序。例如，Java 中的 Arrays.sort()、C 中的 qsort 和 C++ 中的 sort 使用混合排序，其中快速排序是主要的排序算法。
快速排序的不同版本用于识别 K 个最大或最小的元素。

快速排序的优点

快速排序使用分治算法，这使得解决问题更加容易。
快速排序在大型数据集上效果很好。
快速排序的开销很低。这是因为它只需要少量的内存即可工作。
快速排序对缓存友好。这是因为排序工作是在同一数组上完成的。它不会从任何辅助数组复制数据。
对于稳定性不是问题的的大型数据集，快速排序是最快的通用算法。
快速排序使用尾部递归。因此，可以进行所有尾部调用优化。
可以使用快速排序进行并行处理，因为两个子数组可以独立处理。

快速排序的缺点

快速排序的时间复杂度为 O(n²)，当基准选择不当时会出现这种情况。
快速排序不适合小型数据集。
快速排序不是稳定排序。这意味着，（快速排序的结果）两个键相同的元素的相对顺序不会被保留。观察代码中交换元素时未考虑其原始位置。

结论

由于其速度和简单性，快速排序是最广泛使用和最高效的排序算法之一。其原地排序能力与分治方法的结合，使其适用于内存受限的系统和大型数据集。

下一主题归并排序

快速排序算法 (附 Python/Java/C/C++ 程序)

步骤：

算法

快速排序算法的工作原理

Python/Java/C/C++/C# 中的快速排序实现

Python 程序

Java 程序

C++ 程序

C 语言程序

C# 程序

复杂度分析

快速排序的应用

快速排序的优点

快速排序的缺点

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

快速排序算法 (附 Python/Java/C/C++ 程序)

步骤：

算法

快速排序算法的工作原理

Python/Java/C/C++/C# 中的快速排序实现

Python 程序

Java 程序

C++ 程序

C 语言程序

C# 程序

复杂度分析

快速排序的应用

快速排序的优点

快速排序的缺点

结论

相关帖子

排序算法的时间复杂度

选择排序算法

插入排序算法

冒泡排序算法

桶排序算法

堆排序算法

排序算法

计数排序算法

归并排序算法

希尔排序算法

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器