B 树和二叉树的区别

在了解二叉树和 B 树的区别之前，我们应该分别了解二叉树和B 树。

什么是 B 树？

B 树是一种自平衡树，因为其节点按中序遍历排序。与二叉树不同，B 树中的节点可以有两个以上的子节点。B 树的高度是 logMN，其中 M 是树的阶数，N 是节点的数量。B 树的高度自动调整，并且 B 树的高度按特定顺序排序，左侧值最低，右侧值最高。

B 树主要用于存储无法放入主内存的大量数据。当键的数量增加时，数据以块的形式从磁盘读取。众所周知，磁盘访问时间比内存访问时间长。使用 B 树的主要思想是减少磁盘访问次数。B 树上实现的大多数操作，如搜索、删除、插入、最大值、最小值等，都有 O(h) 次磁盘访问，其中 h 是树的高度。B 树是一种非常宽的树。构造 B 树的思想是通过在 B 树节点中附加最大数量的键来尽可能降低树的高度。B 树节点的大小主要等于磁盘块大小。由于树的高度相当低，因此与平衡二叉搜索树（如 AVL 树、红黑树等）相比，磁盘访问显着减少。

下面列出了一些与 B 树相关的重要事实

• B 树中的所有叶节点必须位于同一级别。
• 叶节点上方不应存在任何空子树。
• B 树的高度应尽可能保持较低。

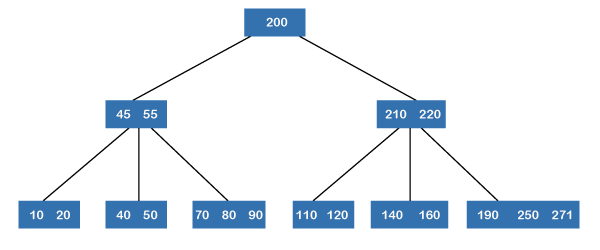在上面的图中，我们可以观察到所有叶节点都存在于同一级别，并且所有非叶节点都是非空子树，其键比其子节点的数量少一个。

什么是二叉树？

二叉树是一种最多包含两个子节点的树。二叉树对节点的度数有一个限制，因为二叉树中的节点不能包含两个以上的子节点。二叉树中最顶部的节点称为根节点，节点主要由两个子树组成，称为左子树和右子树。如果二叉树中的节点不包含任何子节点，则称为叶节点。因此，节点可以有 0、1 或 2 个子节点。可以在二叉树上执行的操作是插入、删除和遍历。

二叉树可分为以下类型

• 满二叉树：二叉树中的每个节点可以有零个或两个子节点。
• 完全二叉树：完全二叉树是一种满二叉树，但有一个条件是所有叶节点都存在于同一深度级别。
• 完全二叉树：完全二叉树是一种所有叶节点都尽可能左对齐的树。
• 平衡二叉树：如果树的高度尽可能小，则称二叉树是平衡的。
• 二叉搜索树：二叉搜索树是一种所有键都已排序以提供更快搜索的树。

它可用于实现表达式求值、解析器、数据压缩算法、存储路由器表、加密应用程序等。

让我们以表格形式了解二叉树和 B 树之间的区别。