DSA 中的超级鸡蛋掉落问题

2025年2月7日 | 阅读 9 分钟

问题陈述

在此问题陈述中，您有一个标有 1 到 n 的 n 层高的建筑，并且我们有 k 个相同的鸡蛋。任何在高于 f 的楼层丢下的鸡蛋都会破裂，任何在或低于楼层 f 丢下的鸡蛋都不会破裂，因为我们知道存在一个楼层 f，其中 0 <= f <= n。在每次移动中，您可以从任何楼层 x（其中 1 <= x <= n）丢下一个完好的鸡蛋。如果鸡蛋破裂，它将不再可用。如果鸡蛋没有破裂，您可以在后续的移动中再次使用它。
返回确定 f 值所需的最小步骤数，以确保准确性。

示例 1

输入： k = 1, n = 2

输出 2

说明

从第一层（第 1 层）开始丢下鸡蛋。
- 如果鸡蛋破裂，则 f = 0。
- 如果鸡蛋没有破裂，则继续下一步。
如果从第一层丢下的鸡蛋没有破裂，则从第二层（第 2 层）丢下鸡蛋。
- 如果鸡蛋破裂，则 f = 1。
- 如果鸡蛋没有破裂，则 f = 2。
在最坏的情况下，我们可能需要两次移动才能确切知道 f 的值。
因此，需要两次移动是最小的。

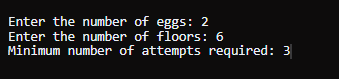
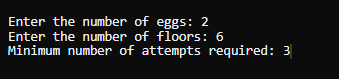
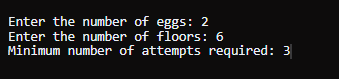
示例 2

输入： k = 2, n = 6

输出 3

说明

首先，从第二层（第 2 层）丢下第一个鸡蛋。

如果鸡蛋破裂，则 f = 1。
如果鸡蛋没有破裂，则继续下一步。

剩下一个鸡蛋，我们可以通过采用二分查找策略来减少查找 f 所需的移动次数。我们可以从一个将剩余楼层分成两半的楼层丢下第二个鸡蛋。在这种情况下，我们可以从第四层（第 4 层）丢下鸡蛋。

如果鸡蛋破裂，则 f = 3。
如果鸡蛋没有破裂，则继续下一步。
如果从第四层丢下的第二个鸡蛋没有破裂，我们可以确定 f = 5。
在最坏的情况下，可能需要 3 次移动才能准确地确定 f 的值。

因此，需要 3 次移动是最小的。

Java 动态规划方法

im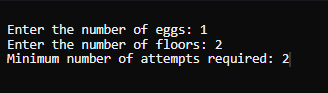port java. util.Scanner; 
public class Solution {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);  
System.out.println("Enter the number of eggs:");
        int k = scanner.nextInt();
System.out.println("Enter the number of floors:");
        int n = scanner.nextInt();
        Solution solution = new Solution();
        System.out.println("Minimum number of attempts required: " + solution.superEggDrop(k, n)); 
scanner.close();
    }
    public int superEggDrop(int k, int n) {
        int[][] dp = new int[k + 1][n + 1];        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= k; j++) {
dp[j][i] = dp[j - 1][i - 1] + dp[j][i - 1] + 1;
                if (dp[j][i] >= n) return i;
            }
        }
        return -1;
    }
}

输出

代码解释

计算最小尝试次数的方法

我们需要初始化一个二维数组 dp 来存储数组子问题的结果。

遍历从 1 到 n 的每一层

迭代从 1 到 k 的每个鸡蛋
- 使用动态规划来计算当前配置的鸡蛋和楼层所需的最小尝试次数。
- 动态规划公式为 dp[j][i] = dp[j - 1][i - 1] + dp[j][i - 1] + 1，表示
  - dp[j - 1][i - 1]：鸡蛋在第 i 层破裂时的尝试次数，少一个鸡蛋和一个楼层
  - dp[j][i - 1]：鸡蛋在第 i 层没有破裂时的尝试次数，鸡蛋数量相同，楼层数少一个。
  - 1：当前尝试
检查当前尝试次数是否超过或等于楼层数。如果是，则返回当前尝试次数。

如果尝试次数未超过楼层数，则返回 -1。

时间复杂度

SuperEggDrop 方法的时间复杂度为 O(k * n)，其中 k 是鸡蛋的数量，n 是楼层的数量。这是因为存在嵌套循环。

空间复杂度

空间复杂度为 O(k * n)，因为它还包含一个维度为 (k+1)* (n+1) 的二维数组 dp，用于存储子问题结果。这会创建一个空间复杂度，其增长与鸡蛋和楼层的数量成正比，从而导致二次空间复杂度。

使用记忆化的 Java 实现

im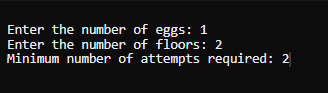port java. util.Scanner; 
public class Solution {
    Integer dp[][];
        public int superEggDrop(int k, int n) {
        dp = new Integer[k + 1][n + 1];
        return sol(k, n);
    }
    public int sol(int k, int n) {
        if (k == 1 || n == 0 || n == 1)
            return n;
                if (dp[k][n] != null)
            return dp[k][n]; 
        int l = 1, h = n;
        int ans = Integer.MAX_VALUE; 
                while (l <= h) {
            int mid = (l + h) / 2;
                        int k1 = sol(k - 1, mid - 1);
            int k2 = sol(k, n - mid);
                        int temp = 1 + Math.max(k1, k2); 
            if (k1 < k2)	
                l = mid + 1;
            else
                h = mid - 1;
            ans = Math.min(temp, ans);
        }
                return dp[k][n] = ans;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in); 
System.out.println("Enter the number of eggs:");
        int k = scanner.nextInt();
System.out.println("Enter the number of floors:");
        int n = scanner.nextInt();
        Solution solution = new Solution();
        System.out.println("Minimum number of attempts required: " + solution.superEggDrop(k, n)); 
scanner.close();
    }
}

输出

代码解释

计算最小尝试次数的方法

初始化一个二维数组 dp 来存储子问题的结果。
调用 sol 方法以递归方式查找解决方案。
返回 sol 方法获得的结果。

递归方法 (sol)

基本情况
- 如果只有一个鸡蛋（k == 1），或者没有楼层（n == 0 或 n == 1），则返回 n（楼层数）。
如果当前状态的解决方案已计算完毕（记忆化），则返回它。
初始化二分查找的下界（l）和上界（h）。
初始化答案（ans）为一个很大的值（Integer.MAX_VALUE）。
执行二分查找以找到最优解
- 计算下界和上界之间的中点（mid）。
- 递归查找鸡蛋破裂和鸡蛋未破裂两种情况的解决方案。
- 计算当前 mid 所需的移动次数。
- 根据二分查找的结果更新答案并调整边界。
记忆化结果并返回它。

时间复杂度

该算法的时间复杂度为 O(k * n * log n)，其中 k 是鸡蛋的数量，n 是楼层的数量。然而，困难来自于嵌套循环，它们处理所有可能的组合，以及这些循环中的二分查找。

空间复杂度

空间复杂度为 O (k n)，因为存储子问题结果的 dp 数组是动态的，需要空间。该数组由元素组成，其维度与鸡蛋和楼层的数量成正比。此外，由于需要重复所有嵌套的鸡蛋和楼层组合的时间，递归栈空间受 O(k * n) 的限制。

使用递归和二分查找的 Java 实现

im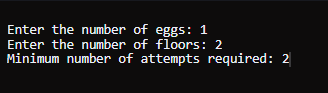port java. util.Scanner; 
public class Solution {
    int dp[][];
        public int superEggDrop(int k, int n) {
                dp = new int[k + 1][n + 1];
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
dp[i][j] = -1;
            }
        }
                int ans = helperBs(k, n);
        return ans;
    }
    public int helper(int eggs, int floors) {
        if (eggs == 1) return floors;
        if (floors == 0 || floors == 1) return floors;
        int ans = Integer.MAX_VALUE;
                for (int k = 1; k <= floors; k++) {
            int ans1 = helper(eggs - 1, k - 1); 
            int ans2 = helper(eggs, floors - k); 
            int ans3 = 1 + Math.max(ans1, ans2); 
            ans = Math.min(ans, ans3);
        }
        return ans;
    }
    public int helperDp(int eggs, int floors) {        
        if (eggs == 1) return floors;
        if (floors == 0 || floors == 1) return floors;
        if (dp[eggs][floors] != -1) return dp[eggs][floors];
                int ans = Integer.MAX_VALUE;
                for (int k = 1; k <= floors; k++) {
            int ans1 = helperDp(eggs - 1, k - 1); 
            int ans2 = helperDp(eggs, floors - k);
            int ans3 = 1 + Math.max(ans1, ans2);
                        ans = Math.min(ans, ans3);
        }
        return dp[eggs][floors] = ans;
    }
    // Memoization technique  with binary search helper method function
    public int helperBs(int eggs, int floors) {
        // Base cases for the helper methiod
        if (eggs == 1) return floors;
        if (floors == 1 || floors == 0) return floors;
        // If we have already calculated, then return the result
        if (dp[eggs][floors] != -1) return dp[eggs][floors];
        // set an  ans with maximum value
        int ans = Integer.MAX_VALUE;
        int low = 1, high = floors, mid = 0;
        // we have to do the Binary search for optimal solution
        while (low <= high) {
            mid = low + (high - low) / 2;
            // then we have to Calculate moves if the egg breaks
            int ans1 = helperBs(eggs - 1, mid - 1);
            //then we have to  Calculate moves if the egg does not break
            int ans2 = helperBs(eggs, floors - mid);
            // we have to Take the maximum moves and add 1 (current move)
            int ans3 = Math.max(ans1, ans2) + 1;
            // we need to Update ans with a minimum value
            ans = (ans > ans3) ? ans3 : ans;
            if (ans1 < ans2) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        // We have to Store the result in the memoization array
        return dp[eggs][floors] = ans;
    }
        public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in); 
System.out.println("Enter the number of eggs:");
        int k = scanner.nextInt();
System.out.println("Enter the number of floors:");
        int n = scanner.nextInt();
        Solution solution = new Solution();
        int result = solution.superEggDrop(k, n); 
System.out.println("Minimum number of attempts required :" + result); 
scanner.close();
    }
}

输出

代码说明

递归辅助方法 (helper)

基本情况
- 如果只有一个鸡蛋（k == 1），则返回楼层数（n）。
- 如果没有楼层（n == 0）或只有一层（n == 1），则返回楼层数（n）。
初始化 ans
- 初始化一个变量 ans 来存储最小尝试次数，从最大值开始。
遍历所有楼层
- 迭代每个楼层（k）以查找最小移动次数。
- 对于每个楼层，计算鸡蛋破裂（ans1）和鸡蛋未破裂（ans2）的最小移动次数。
- 计算总移动次数（ans3）为 ans1 和 ans2 之间的最大移动次数，再加上 1（当前移动）。
- 将 ans 更新为当前值与先前 ans 之间的最小值。
返回最小移动次数（ans）。

记忆化辅助方法 (helperDp)

基本情况和记忆化
- 与 helper 方法相同。
- 如果当前状态的结果已计算，则从记忆化数组中返回它。
递归计算
- 与 helper 方法相同。
记忆化结果
- 将结果记忆化到记忆化数组中。
- 返回记忆化的结果。

带有二分查找的记忆化辅助方法 (helperBs)

基本情况和记忆化
- 与 helperDp 方法相同。
通过二分查找优化解决方案
- 执行二分查找以找到最优解决方案。
- 根据递归调用的结果调整搜索范围。
记忆化结果
- 将结果记忆化到记忆化数组中。
- 返回记忆化的结果。

时间复杂度

该算法的时间复杂度陈述为 O(k * n * log n) 的乘积，其中 k 和 n 分别是鸡蛋和楼层的数量。这个问题源于两个循环，它们都是递归的，因此是嵌套的；二分查找过程在 helperBs 方法中加剧了这个问题。

空间复杂度

该算法的空间复杂度为 O(k * n)，其中 k 是鸡蛋的数量，n 是楼层的数量。在此内存槽中，存在一个填充了记忆化（DP）的数组，旨在确保每次计算至少一次就足够了。

下一主题每个程序员都必须知道的顶级数据结构

DSA 中的超级鸡蛋掉落问题

问题陈述

示例 1

说明

示例 2

说明

Java 动态规划方法

代码解释

时间复杂度

空间复杂度

使用记忆化的 Java 实现

代码解释

递归方法 (sol)

时间复杂度

空间复杂度

使用递归和二分查找的 Java 实现

代码说明

时间复杂度

空间复杂度

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

DSA 中的超级鸡蛋掉落问题

问题陈述

示例 1

说明

示例 2

说明

Java 动态规划方法

代码解释

时间复杂度

空间复杂度

使用记忆化的 Java 实现

代码解释

递归方法 (sol)

时间复杂度

空间复杂度

使用递归和二分查找的 Java 实现

代码说明

时间复杂度

空间复杂度

相关帖子

数据结构中的逆序对问题

二叉搜索树前序遍历的叶节点

C++ 中重新排序路线以使所有路径都通往城市零

ArrayList vs LinkedList

计算增加的四元组数量

DSA 中的丑陋数字

单调栈导论

哈希及其应用

从目标节点开始烧毁二叉树

股票买卖问题

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器