使用 Python 对矩阵数据结构执行不同操作

本文将深入探讨使用 Python 和 NumPy 进行矩阵运算。内容将涵盖矩阵概念、Python 中的表示方法，以及加法、减法、乘法、转置等运算。还将讨论矩阵分解、求解线性方程组等高级主题。

矩阵是由行和列组织的数字网格。它被广泛应用于计算机科学、工程、物理学和经济学等各个领域。在编程中，矩阵对于线性代数任务的计算和数据处理至关重要。

Python 是一种编程语言，通过其内置库支持矩阵操作。NumPy 库（称为 Numerical Python）提供了一系列用于矩阵运算的工具，使其在科学家、工程师和数据分析师中广受欢迎。

通过掌握 Python 中的这些矩阵运算，您将能够提高数值计算和数据处理方面的技能。这些知识将帮助您高效地解决问题，无论您是在进行科学模拟、开发机器学习算法还是执行数据分析任务。

什么是矩阵数据结构？

矩阵就像一个矩形数组，其中的元素按行和列排列。它是线性代数中的一个基本数据结构，广泛应用于计算机科学、工程、物理学和经济学等各个领域。矩阵可以以表格形式表示和处理数据，使其成为数值计算和数据分析任务的关键。

矩阵的性质

矩阵具有几个重要的性质，它们定义了它们的结构和行为。理解这些性质对于在各种应用中有效地使用矩阵至关重要。矩阵的关键性质如下：

1. 维度

矩阵的维度是指其包含的列数和行数。矩阵通常用 m x n 的表示法表示，其中 m 是行数，n 是列数。

例如，一个具有 3 行 4 列的矩阵的维度为 3 x 4。

在这个例子中，matrix_A 的维度是 3 x 4，意味着它有 3 行和 4 列。

2. 阶

矩阵的阶是其维度的总和。例如，一个维度为 m x n 的矩阵的阶是 m + n。阶代表矩阵中元素的总数。

例如，一个维度为 2 x 3 的矩阵的阶是 2 + 3 = 5。

3. 方阵

如果一个矩阵的行数和列数相同，则称其为方阵。换句话说，方阵的维度为 n x n，其中 n 是行数和列数。

在上例中，matrix_B 是一个 3 x 3 的方阵。

4. 对角线

方阵的对角线是从左上角到右下角的元素集合。这些元素具有相同的行和列索引。

输出

Diagonal elements: 1 5 9

5. 对称矩阵

如果一个方阵等于其转置（行和列互换），则称其为对称矩阵。换句话说，对称矩阵可以写成 A = A.T。

输出

Matrix D is not symmetric

6. 单位矩阵

单位矩阵是一个方阵，其对角线上的元素为 1，其余元素均为 0。它用字母 I 表示。当一个矩阵乘以相同维度的单位矩阵时，结果是它本身。

输出

Identity Matrix:
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

7. 零矩阵

零矩阵是一个所有元素都为 0 的矩阵。它通常用符号 0 或 O 表示。

输出

Zero Matrix:
 [[0. 0. 0.]
 [0. 0. 0.]]

8. 奇异矩阵

如果一个方阵的行列式等于零，则称其为奇异矩阵。奇异矩阵没有逆矩阵，它们表示具有无解或无穷多解的线性方程组。

输出

Matrix E is non-singular

9. 正交矩阵

如果一个方阵的转置等于其逆矩阵，则称其为正交矩阵。正交矩阵在线性代数、几何学以及数学和物理学的各个领域都有重要的应用。

输出

Matrix F is orthogonal

这些矩阵性质在各种数学运算和应用中起着至关重要的作用。理解它们对于有效使用矩阵和正确解释矩阵计算结果至关重要。

矩阵的不同运算

1. 加法和减法

• 当您要添加或减去两个矩阵时，请确保它们的维度匹配，即行数和列数相同。
• 加法和减法是通过分别取两个矩阵的每个元素并将它们相应地相加或相减来完成的。
• 示例：如果 A = [[1, 2], [3, 4]] 且 B = [[5, 6], [7, 8]]，则 A + B = [[6, 8], [10, 12]] 且 A - B = [[-4, -4], [-4, -4]]。

2. 标量乘法

• 标量是指一个值。
• 标量乘法包括将矩阵的每个元素乘以标量值。
• 例如，如果我们有一个矩阵 A 为 [[1 2] [3, 4]] 且标量 k 等于 2，则 k 乘以 A 的结果是 [[2, 4] [6, 8]]。

3. 矩阵乘法

• 矩阵乘法涉及两个矩阵之间的运算。
• 要定义两个矩阵之间的乘法，第一个矩阵的列数必须等于第二个矩阵的行数。
• 结果是一个维度为 (第一个矩阵的行数) x (第二个矩阵的列数) 的矩阵。
• 例如：如果 A 是 [[1, 2] [3, 4]] 且 B 是 [[5, 6] [7, 8]]，则 A 乘以 B 的结果是 [[19,22] [43,50]]。

4. 转置

• 转置通过交换矩阵中的行和列来形成一个新排列。
• 当您有一个维度为 m x n 的矩阵 A 时，其转置 A^T 的维度将是 n x m。
• 例如，如果我们有一个 A = [[1, 2 3] [4, 5 6]]，则 A^T 将是 [[1, 4] [2, 5] [3, 6]]。

5. 行列式

• 行列式是使用矩阵元素计算出的一个值。
• 它有助于确定一个方阵是否可逆（是否有逆矩阵）。
• 可逆矩阵的行列式为零。

6. 逆矩阵

• 方阵 A 的倒数，表示为 A^-1，是一个满足条件 A * A^-1 = A^-1 * A = I 的矩阵，其中 I 是单位矩阵。
• 逆矩阵用于解决方程组和确定变换的逆。
  • 当且仅当其行列式非零时，矩阵才有逆矩阵。

7. 矩阵分解

• 矩阵分解将一个矩阵分解成更简单的部分或因子。
• 常见的分解包括 LU 分解（用于求解线性方程组）、QR 分解（用于最小二乘问题）和奇异值分解 (SVD)（用于数据压缩和降维）。

8. 特征值和特征向量

• 特征值和特征向量是线性代数中的重要概念，在各个领域都有广泛的应用。
• 方阵 A 的特征向量 v 是一个非零向量，满足 A * v = λ * v，其中 λ 是一个称为特征值的标量。
• 特征值和特征向量用于求解微分方程、分析动态系统以及理解线性变换的行为。

9. 矩阵范数

• 矩阵范数是为矩阵分配非负标量值的函数，它提供了矩阵“大小”或“幅度”的度量。
• 常见的范数包括 Frobenius 范数（基于元素平方和的平方根）和谱范数（基于最大奇异值）。
• 矩阵范数在数值分析、优化和误差分析中很有用。

10. 矩阵因子分解

• 矩阵因子分解将一个矩阵表示为具有特定性质的两个或多个矩阵的乘积。
• 示例包括 Cholesky 分解（用于正定矩阵）、LU 分解（用于求解线性方程组）和 QR 分解（用于最小二乘问题和正交变换）。
• 因子分解对于高效的计算算法和数值稳定性至关重要。

这些矩阵运算是线性代数、数值分析、信号处理、机器学习和科学计算等各个领域的基石。正确理解和实现这些运算对于解决复杂问题和开发高效算法至关重要。

加法

矩阵加法算法

1. 检查两个矩阵的维度是否相等（行数和列数相同）。
2. 如果维度不相等，则返回一条错误消息，表明无法进行矩阵加法。
3. 创建一个具有与输入矩阵相同维度的新空矩阵来存储结果。
4. 遍历矩阵中的每个元素：a. 访问输入矩阵中对应的元素。b. 相加元素。c. 将结果存储在结果矩阵的相应位置。
5. 返回结果矩阵。

输出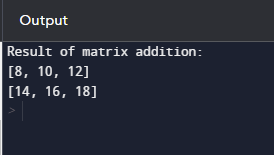

说明

1. 函数定义：程序定义了一个名为 add_matrices 的函数，该函数以两个矩阵作为输入。
2. 维度检查：它检查输入矩阵是否具有相同的行数和列数。
   • 如果维度不同，它将返回一条错误消息。
3. 结果矩阵创建：如果维度相等，则创建一个新的空矩阵来存储结果。
   • 新矩阵具有与输入矩阵相同的维度。
4. 逐元素相加：它使用循环遍历输入矩阵中的每个元素。
   • 对于每对对应的元素，它执行加法。
   • 总和存储在结果矩阵的相应位置。
5. 返回结果：添加完所有元素后，函数返回结果矩阵。
6. 示例用法：程序提供了使用列表的列表定义的两个矩阵的示例。
7. 函数调用：它以示例矩阵作为参数调用 add_matrices 函数。
8. 输出处理：它检查返回值。
   • 如果它是错误消息（字符串），则打印消息。
   • 如果它是矩阵（列表的列表），则逐行打印结果。
9. 假设：程序假设输入矩阵是有效的，并表示为列表的列表。在生产环境中可能需要额外的错误处理。
   • 在生产环境中可能需要额外的错误处理。

减法

矩阵减法算法

1. 检查两个矩阵的维度是否相等（行数和列数相同）。
2. 如果维度不相等，则返回一条错误消息，表明无法进行矩阵减法。
3. 创建一个具有与输入矩阵相同维度的新空矩阵来存储结果。
4. 遍历矩阵中的每个元素：a. 访问输入矩阵中对应的元素。b. 相减元素（第一个矩阵元素 - 第二个矩阵元素）。c. 将结果存储在结果矩阵的相应位置。
5. 返回结果矩阵。

输出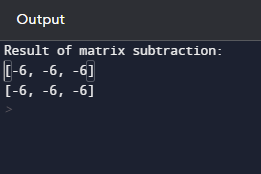

说明

1. 程序定义了一个名为 subtract_matrices 的函数，该函数以两个矩阵作为输入。
2. 它检查输入矩阵是否具有相同的行数和列数。
   • 如果维度不同，它将返回一条错误消息。
3. 如果维度相等，则创建一个新的空矩阵来存储结果。
   • 新矩阵具有与输入矩阵相同的维度。
4. 它使用循环遍历输入矩阵中的每个元素。
   • 对于每对对应的元素，它执行减法（第一个矩阵元素 - 第二个矩阵元素）。
   • 差值存储在结果矩阵的相应位置。
5. 减去所有元素后，函数返回结果矩阵。
6. 程序提供了使用列表的列表定义的两个矩阵的示例。
7. 它以示例矩阵作为参数调用 subtract_matrices 函数。
8. 它检查返回值。
   • 如果它是错误消息（字符串），则打印消息。
   • 如果它是矩阵（列表的列表），则逐行打印结果。
9. 程序假设输入矩阵是有效的，并表示为列表的列表。
   • 在生产环境中可能需要额外的错误处理。

标量乘法

矩阵标量乘法算法

• 将标量值（单个数字）和矩阵作为输入。
• 创建一个具有与输入矩阵相同维度的新空矩阵来存储结果。
• 遍历输入矩阵中的每个元素：a. 将标量值与当前元素相乘。b. 将结果存储在结果矩阵的相应位置。
• 返回结果矩阵。

输出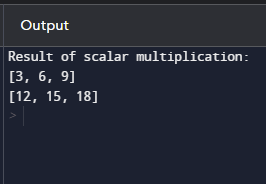

说明

1. 程序定义了一个名为 scalar_multiply 的函数，该函数以标量值和矩阵作为输入。
2. 它获取输入矩阵的行数和列数。
3. 它创建一个具有与输入矩阵相同维度的新空矩阵来存储结果。
4. 它使用循环遍历输入矩阵中的每个元素。
   • 对于每个元素，它将标量值与该元素相乘。
   • 乘积存储在结果矩阵的相应位置。
5. ：将所有元素与标量相乘后，函数返回结果矩阵。
6. 程序提供了使用列表的列表定义的标量值和矩阵的示例。
7. 它以示例标量值和矩阵作为参数调用 scalar_multiply 函数。
8. 它逐行打印标量乘法的结果。
9. 程序假设输入矩阵是有效的，并表示为列表的列表。
   • 在生产环境中可能需要额外的错误处理。

矩阵乘法

矩阵乘法算法

1. 接受两个矩阵作为输入。
2. 检查第一个矩阵的列数是否等于第二个矩阵的行数。如果不相等，则返回一条错误消息，表明无法进行矩阵乘法。
3. 要存储结果，请创建一个新的空矩阵，其维度为（第一个矩阵的行数）x（第二个矩阵的列数）。
4. 遍历第一个矩阵的行：a. 遍历第二个矩阵的列：i. 初始化一个变量来存储对应元素的乘积。ii. 遍历第一个矩阵的列和第二个矩阵的行：- 将对应元素相乘并累积乘积。iii. 将累积的乘积存储在结果矩阵的相应位置。
5. 返回结果矩阵。

输出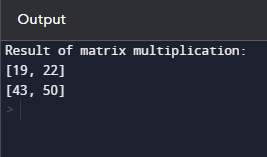

说明

• 程序定义了一个名为 multiply_matrices 的函数，该函数接受两个矩阵（matrix1 和 matrix2）作为输入。
• 在该函数内部，它首先通过确保第一个矩阵的列数与第二个矩阵的行数匹配来检查矩阵乘法是否可能。
• 如果维度不兼容，它将返回一个字符串形式的错误消息。
• 如果维度兼容，则创建一个新的空矩阵（result），其维度为（第一个矩阵的行数）x（第二个矩阵的列数），以存储矩阵乘法的结果。
• 然后，函数使用嵌套循环执行矩阵乘法。
• 外层循环遍历第一个矩阵的行。
• 对于第一个矩阵中的每一行，内层循环遍历第二个矩阵的列。
• 对于行和列的每种组合，第三个循环遍历第一个矩阵的列和第二个矩阵的行。
• 在此第三个循环中，将两个矩阵中的对应元素相乘，并将乘积累积到结果矩阵的相应位置。
• 计算完结果矩阵的所有元素后，函数返回结果矩阵。
• 然后，程序提供了两个矩阵（matrix1 和 matrix2）的示例用法，它们被定义为列表的列表。
• 使用这些示例矩阵作为参数调用 multiply_matrices 函数，并将结果存储在 result 变量中。
• 程序检查返回的值（result）是否是字符串类的一个实例（表示错误消息）。
• 如果结果是字符串，则打印错误消息。
• 如果结果不是字符串（即，是一个有效的矩阵），则打印标题“矩阵乘法结果：”，然后逐行打印结果矩阵。
• 程序假设输入矩阵是有效的，并表示为列表的列表。在生产环境中可能需要额外的错误处理。

Transpose

矩阵转置算法

1. 接受一个矩阵作为输入。
2. 获取输入矩阵的行数和列数。
3. 创建一个新的空矩阵，其维度为（输入矩阵的列数）x（输入矩阵的行数），以存储转置。
4. 遍历输入矩阵的行：a. 遍历输入矩阵的列：i. 将输入矩阵中的元素复制到转置矩阵的相应位置（通过交换行和列索引）。
5. 返回转置矩阵。

输出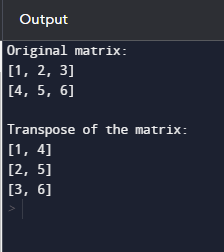

说明

• 定义一个名为 transpose_matrix 的函数，该函数以矩阵作为输入。
• 使用 len 函数获取输入矩阵的行数和列数。
• 创建一个新的矩阵 transpose，其维度为（输入矩阵的列数）x（输入矩阵的行数），以存储转置。
• 新矩阵的初始元素都为 0。
• 使用嵌套循环执行转置
• 遍历输入矩阵的行。
• 对于每一行，遍历输入矩阵的列。
• 对于每个元素，将输入矩阵中的元素复制到转置矩阵的相应位置（通过交换行和列索引）。
• 返回转置矩阵。
• 提供使用列表的列表定义的矩阵的示例用法。
• 以示例矩阵作为参数调用 transpose_matrix 函数，并将结果存储在 result 中。
• 逐行打印原始矩阵。
• 打印一个换行符分隔符。
• 逐行打印矩阵的转置。