使用 Hoare 分区法的快速排序

2025年03月17日 | 阅读 9 分钟

在本文中，我们将讨论如何使用Hoare分区实现快速排序，其应用以及Hoare分区方案相对于Lomuto分区方案的优势。

快速排序

这种排序算法的思想是选择一个元素（枢轴元素）并找到它在数组中的正确位置，确保其左边的元素必须更小，右边的元素必须更大。对左子数组和右子数组递归重复相同的过程，直到数组排序完成。

它在内存使用和时间方面更高效，是一种广泛使用的搜索算法。它采用分治法对数组进行排序。

伪代码

function quickSort(arr, low, high):
	if low < high:
		pivot_index = hoaresPartition(arr, n , low, high)
		quicksort(arr, low, pivot_index-1)
		quicksort(arr, pivot_index+1, high)

Hoare分区方案

查尔斯·安东尼·理查德·霍尔爵士开发了快速排序算法，Lomuto和Hoare的分区方案都是他提出的。与Lomuto分区（它使用一个枢轴元素并基于它对数组进行分区）不同，Hoare分区使用两个指针，它们沿相反方向遍历数组，并进行必要的交换直到指针相遇。

这种分区方案减少了交换次数，从而实现了时间高效的性能。其工作原理如下：

伪代码

function hoarePartition(arr, low, high):
    pivot = arr[low]
    i = low - 1 // Initialize left pointer
    j = high + 1 // Initialize right pointer

    while true:
        do:
            i = i + 1
        while arr[i] < pivot // Increment i while arr[i] is less than the pivot

        do
            j = j - 1
        while arr[j] > pivot // Decrement j while arr[j] is greater than the pivot

        if i >= j: // If i and j meet or cross each other
            return j // Return partition index

        swap(arr[i], arr[j])

分区索引左边的元素将小于或等于枢轴。分区索引右边的元素将大于或等于枢轴。

时间复杂度分析

平均情况分析

Time Complexity: T(N) = O(N logN)
Recurrence Relation: T(N) = T(N/10) + T(9N/10) + O(N)

在平均情况下，我们认为分区没有将数组公平地分成两半。我们考虑第一半有1/10的元素，第二半有9/10的元素。

最坏情况分析

Time Complexity: T(N) = O(N2)
Recurrence Relation: T(N) = T(N-1) + O(N)

当我们传递一个按升序或降序排序的数组时，它的性能会更差。在最坏情况下，分区函数每次都选择最小或最大的元素，导致性能不佳。

空间复杂度分析

快速排序算法是一种原地排序算法，不需要额外的空间来存储元素。它需要辅助空间用于递归调用栈。

在最坏情况下，递归调用栈需要 Θ(n) 空间。

下面是递归调用栈的快照

Python 实现

# Quick Sort Function
def quickSort(arr, low, high):
    # Base case: if the sub-array has more than one element
    if low < high:
        # Partition the array using Hoare's Partition scheme
        i = hoarePartition(arr, low, high)
        
        # Recursively sort the left sub-array
        quickSort(arr, low, i)
        
        # Recursively sort the right sub-array
        quickSort(arr, i + 1, high)

# Hoare's Partition Function
def hoarePartition(arr, low, high):
    # Choose the first element as the pivot
    pivot = arr[low]
    
    # Initialize pointers:
    left = low - 1 # Left Pointer
    right = high + 1 # Right Pointer

    # Start an infinite loop to traverse the array and rearrange elements
    while True:
        # Move the left pointer to the right until
        # an element greater than or equal to the pivot is found
        left += 1
        while arr[left] < pivot:
            left += 1
        
        # Move the right pointer to the left until
        # an element less than or equal to the pivot is found
        right -= 1
        while arr[right] > pivot:
            right -= 1
        
        # If the left pointer crosses or becomes equal
        # to the right pointer, the partitioning is complete
        if left >= right:
            # Return the right pointer position
            # as the index for the next partition
            return right
        
        # Swap the elements at the left and right pointers
        arr[left], arr[right] = arr[right], arr[left]

# Sample array
arr = [10, 2, 16, 22, 35, 17, 26, 3, 9, 13]
print(f"Unsorted Array: {arr}")

# Call quickSort to sort the array
quickSort(arr, 0, 9)
print(f"Sorted Array: {arr}")

输出

说明

我们有一个列表：arr = [10, 2, 16, 22, 35, 17, 26, 3, 9, 13]，n = 10。

调用： quickSort(arr, 0, 9)

这里，low = 0 且 high = 9，low 小于 high

quickSort()函数调用 hoarePartition(arr, 0, 9)。当它返回分区索引时，quickSort()使用以下参数调用自身：quickSort(arr, low, i) 和 quickSort(arr, i+1, high)。

整个思想在于分区方案。因此，理解Hoare分区方案很重要。您可以在此处找到使用Lomuto分区法的快速排序的简要说明。

现在让我们了解hoarePartition()函数的工作原理。

def hoarePartition(arr, low, high):
    pivot = arr[low]
    left = low - 1 # Left Pointer
    right = high + 1 # Right Pointer

它选择子数组的第一个元素作为枢轴来比较其他元素。这里，枢轴 = arr[0] = 10，左右指针初始化如下：

left = -1

right = 10

然后它开始一个无限循环来遍历数组。

left += 1
left = -1 + 1 = 0

它初始化 left = 0 指针并将其向右移动，直到找到一个大于或等于枢轴的元素。

while arr[left] < pivot:
    left += 1

left = 0

arr[left] = 10 等于枢轴 = 10：由于while条件不满足，它在 left = 0 处中断循环。

right -= 1
right = 10 - 1 = 9

然后它初始化 right = 9 并将其向左移动，直到找到一个小于或等于枢轴的元素。

while arr[right] > pivot:
    right -= 1

right = 8

arr[right] = 9 小于枢轴 = 10：由于while条件不满足，它在 right = 8 处中断循环。

if left >= right:
    return right

然后我们检查左指针是否越过右指针。这里，if条件不满足。

然后我们交换 left = 0 和 right = 8 处的元素。

由于左指针小于右指针，它开始下一次迭代。

在第二次迭代中

它交换 left = 2 和 right = 7 处的元素：swap(arr[left] = 16, arr[right] = 3)

在第三次迭代中

左指针停在索引3，arr[left] = 22，右指针停在索引2，arr[right] = 3。

if left >= right:
    return right

在此迭代中，左指针变得大于右指针，hoarePartition()返回 right = 2。

让我们快速回顾一下其他一些函数调用。

调用：quicksort(arr, 0, 2)

在此调用中，hoarePartition()交换 (9, 3) 并返回 1，并根据需要进行函数调用。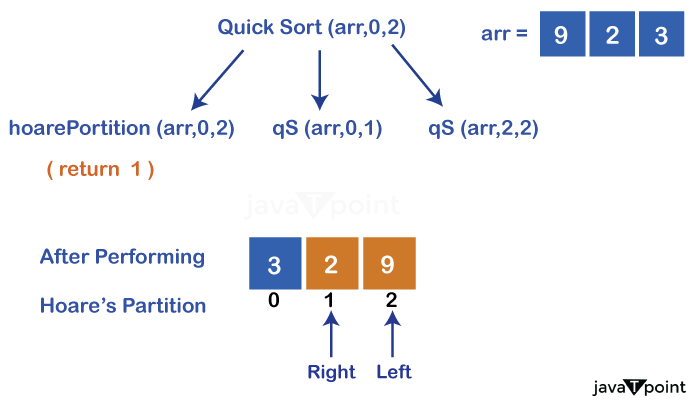

上述递归树展示了如何进行后续函数调用。

调用：quicksort(arr, 3, 9)

在此调用中，hoarePartition()首先交换 (22, 13)，然后交换 (35, 10)，最后交换 (26, 16) 并返回 6。

这个过程对所有可能的递归调用递归重复，最终数组得到排序。

C++ 实现

#include <iostream>
using namespace std;

// Function to swap two elements in the array
void swap(int arr[], int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// Function to print the elements of the array
void printArray(int arr[], int n){
    for (int i = 0; i < n; i++){
        cout << arr[i] << " ";
    }
    cout << endl;
}

// Function implementing Hoare's Partition for Quick Sort
int hoarePartition(int arr[], int low, int high){
    // Choose the first element as pivot element
    int pivot = arr[low];
    
    // Initialize two pointers:
    int left = low - 1; // Left Pointer
    int right = high + 1; // Right Pointer

    // Start an infinite loop to traverse the array
    while (1) {
        // Move left pointer to the right until
        // an element greater than or equal to the pivot is found
        left++;
        while (arr[left] < pivot){
            left++;
        }
        
        // Move right pointer to the left until
        // an element less than or equal to the pivot is found
        right--;
        while (arr[right] > pivot){
            right--;
        }
        
        // If the left pointer crosses or becomes equal to the right pointer,
        // the partitioning is complete
        if (left >= right){
            // Return the right pointer position as the index
            // for the next partition
            return right;
        }
        
        // Swap the elements at the left and right pointers
        swap(arr, left , right);
    }
}

// Function implementing Quick Sort using Hoare's Partition
void quickSort(int arr[], int low, int high){
    // Base case: if the sub-array has more than one element
    if (low < high){
        // Partition the array using Hoare's Partition
        // and get the index of the pivot
        int i = hoarePartition(arr, low, high);
        
        // Recursively sort the left sub-array
        // (elements before the pivot)
        quickSort(arr, low, i);
        
        // Recursively sort the right sub-array
        // (elements after the pivot)
        quickSort(arr, i+1, high);
    }
}

int main() {
    // Write C++ code here
    int arr[] = {14, 8, 22, 16, 12, 5, 6, 25, 2, 9};
    int n = 10;
    
    // Print array
    cout << "Unsorted Array: ";
    printArray(arr, 10);
    
    // Call quickSort to sort the array
    quickSort(arr, 0, 9);
    
    // Print array
    cout << "Sorted Array: ";
    printArray(arr, 10);

    return 0;
}

输出

C 语言实现

 #include <stdio.h>

// Function to swap two elements in the array
void swap(int arr[], int i, int j){
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// Function to print the elements of the array
void printArray(int arr[], int n){
    for (int i = 0; i < n; i++){
        printf("%d ",arr[i]);
    }
    printf("\n");
}

// Function implementing Hoare's Partition for Quick Sort
int hoarePartition(int arr[], int low, int high){
    // Choose the first element as pivot element
    int pivot = arr[low];
    
    // Initialize two pointers:
    int left = low - 1; // Left Pointer
    int right = high + 1; // Right Pointer

    // Start an infinite loop to traverse the array
    while (1) {
        // Move left pointer to the right until
        // an element greater than or equal to the pivot is found
        left++;
        while (arr[left] < pivot){
            left++;
        }
        
        // Move right pointer to the left until
        // an element less than or equal to the pivot is found
        right--;
        while (arr[right] > pivot){
            right--;
        }
        
        // If the left pointer crosses or becomes equal to the right pointer,
        // the partitioning is complete
        if (left >= right){
            // Return the right pointer position as the index
            // for the next partition
            return right;
        }
        
        // Swap the elements at the left and right pointers
        swap(arr, left , right);
    }
}

// Function implementing Quick Sort using Hoare's Partition
void quickSort(int arr[], int low, int high){
    // Base case: if the sub-array has more than one element
    if (low < high){
        // Partition the array using Hoare's Partition
        // and get the index of the pivot
        int i = hoarePartition(arr, low, high);
        
        // Recursively sort the left sub-array
        // (elements before the pivot)
        quickSort(arr, low, i);
        
        // Recursively sort the right sub-array
        // (elements after the pivot)
        quickSort(arr, i+1, high);
    }
}

int main() {
    // Write C++ code here
    int arr[] = {6, 8, 2, 16, 22, 3, 9, 33, 6, 17};
    int n = 10;
    
    // Print array
    printf("Unsorted Array: ");
    printArray(arr, 10);
    
    // Call quickSort to sort the array
    quickSort(arr, 0, 9);
    
    // Print array
    printf("Sorted Array: ");
    printArray(arr, 10);

    return 0;
}

输出

Hoare分区相对于Lomuto分区的优势

Hoare分区相对于Lomuto分区具有多项优势，使其在某些场景下成为首选

更少的交换次数： 它减少了分区过程中所需的交换次数。交换元素是计算密集型操作，减少交换次数可提高算法的整体性能。
更高的效率： 由于交换次数更少，它的性能通常优于Lomuto分区。它比Lomuto快得多，使其成为更有效的分区方案。
更好地处理重复元素： Lomuto分区不能有效处理重复元素。相反，它能更有效地处理重复元素，从而实现更平衡的分区和提高整体性能。

然而，与Lomuto分区一样，它也不能保证稳定性。相同元素的顺序可能会改变。

结论

快速排序是一种原地排序算法，遵循分治法。它利用了Hoare分区，提供了出色且时间高效的分区。它提高了快速排序算法的性能，导致比Lomuto分区更快的排序时间。快速排序是高效排序大型数据集的流行选择。当稳定性不那么重要时，它优于归并排序。它对缓存友好，因为它对所有数据进行操作，并且所有数据都可以存储在缓存中。

下一个主题最长公共子串

← 上一个下一个 →

使用 Hoare 分区法的快速排序

快速排序

伪代码

Hoare分区方案

时间复杂度分析

空间复杂度分析

Python 实现

C++ 实现

C 语言实现

Hoare分区相对于Lomuto分区的优势

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

使用 Hoare 分区法的快速排序

快速排序

伪代码

Hoare分区方案

时间复杂度分析

空间复杂度分析

Python 实现

C++ 实现

C 语言实现

Hoare分区相对于Lomuto分区的优势

结论

相关帖子

矩阵的置换行

二分指数

访问数组位置以最大化分数

产品数组谜题

K 中心问题 (贪心近似算法)

线段树 - 给定范围的求和

合并两棵二叉树

何时应使用 List vs LinkedList

如果给出两种遍历序列，能否构建二叉树

巧克力分配问题

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器