数据结构中图的类型

图数据结构用于存储计算所需的数据，以解决许多计算机编程问题。图用于解决现实世界中的问题，其中问题领域被表示为网络，例如**电话网络、电路网络、领英、Facebook**等。

在计算机科学中，图是一种抽象数据类型，用于在数学图论中实现无向图和有向图的概念。

图数据结构由有限的、可能可变的顶点集（也称为节点或点）以及无序对集（对于无向图）或有序对集（对于有向图）组成。这些对被称为边、链接或线（在有向图中），也称为箭头或弧。顶点可以是内部图元素，也可以是通过整数索引或引用表示的外部项。

因此，根据这些节点和顶点的不同位置，存在不同类型的图，例如：

• 空图
• 平凡图
• 无向图
• 有向图
• 连通图
• 不连通图
• 正则图
• 完全图
• 圈图
• 有环图
• 无环图
• 有限图
• 无限图
• 二分图
• 平面图
• 简单图
• 多重图
• 伪图
• 欧拉图
• 哈密顿图

空图

空图也称为零阶图。“**空图**”一词指的是边集为空的图。换句话说，空图没有边，空图存在于图中只有孤立的顶点。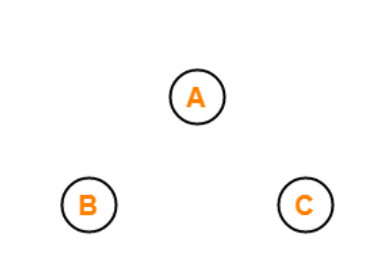

上面显示的图像是空图或零图，因为它在图的三个顶点之间没有边。

平凡图

如果一个图只有一个顶点，则称该图为平凡图。平凡图是最小可能图，它可以通过最少数量的顶点（仅一个顶点）创建。

上面是一个平凡图的例子，它在整个图中只有一个名为顶点 A 的顶点。

无向图

如果图中任意节点之间的所有边都是无向的，则称该图为无向图。无向边意味着图的边无法确定其起点和终点。要称一个图为无向图，图的所有边都必须是无向的。无向图的所有边都没有方向。

上面显示的图是一个不连通图的示例。该图称为不连通图，因为它有四个顶点，分别称为顶点 A、顶点 B、顶点 C 和顶点 D。这些顶点之间也有正好四个边。并且图中的不同节点之间存在的所有顶点都是无向的，这意味着边没有特定的方向。

例如，顶点 A 和顶点 B 之间的边没有方向，因此我们无法确定顶点 A 和顶点 B 之间的边是从顶点 A 还是顶点 B 开始的。同样，我们也无法确定这些节点之间这条边的终点。

有向图

有向图的另一个名称是“digraphs”。如果图中任意顶点或节点之间的所有边都有方向，则称该图为有向图或“digraph”。有向边是指有方向的图的边，可以确定它从哪个节点开始，在哪个节点结束。

要称一个图为有向图或“digraph”，图的所有边都必须是有方向的。有向图或“digraph”的所有边都有一个方向，从一个顶点开始，到另一个顶点结束。

上面显示的图是一个连通图的示例。该图称为连通图，因为它有四个顶点，分别称为顶点 A、顶点 B、顶点 C 和顶点 D。这些顶点之间也有正好四个边，并且图中的不同节点之间存在的所有顶点都有方向（或指向某些顶点），这意味着边被赋予了特定的方向。

例如，考虑顶点 D 和顶点 A 之间的边。这条边显示了一个箭头指向顶点 A，这意味着这条边从顶点 D 开始，到顶点 A 结束。

连通图

一个图要被标记为连通图，图中的每对顶点之间必须至少存在一条路径。换句话说，如果我们从一个顶点开始，我们应该能够移动到该图中的任何一个顶点，这意味着图的所有顶点之间至少存在一条路径。

上面显示的图是一个连通图的示例，因为我们可以从图中的任意一个顶点开始，然后移动到图中的其他任意一个顶点。将有至少一条路径用于遍历图。

例如，如果我们从顶点 B 开始，然后遍历到顶点 H，there are various paths for traversing. One of the paths is

同样，从顶点 B 到顶点 H，还有其他遍历图的路径。图中所有节点之间至少存在一条路径。换句话说，图的所有顶点或节点都通过边或多条边相互连接。

不连通图

如果一个图在至少一对顶点之间不存在任何路径，则该图称为不连通图。换句话说，如果我们从图中的任意一个顶点开始，并尝试移动到图中的其他顶点，并且没有任何一条路径可以移动到该顶点，那么这种情况就是不连通图。如果这对顶点中的任何一个之间没有路径，则称为**不连通图。

上面显示的图是不连通图。上面的图称为不连通图，因为至少有一对顶点之间不存在从任一节点开始的遍历路径。

例如，如果我们想从顶点 A 遍历到顶点 G，那么它们之间不存在单一路径。换句话说，图的所有顶点或节点都没有通过边或多条边相互连接，以便可以遍历。

正则图

一个图要被称为正则图，它必须满足一个主要条件：所有图的顶点都应该具有相同的度。顶点的度数是指与特定顶点相关联的节点数量。如果所有图的节点都具有相同的度值，则该图称为**正则图**。如果一个图的所有顶点的度数都为 6，则该图称为 6-正则图。如果一个图中的所有顶点的度数都为“k”，则称为“**k-正则图”。

上面显示的图是正则图。在图 1 中，有三个顶点，分别称为顶点 A、顶点 B 和顶点 C。图 1 中的所有顶点，每个节点的度数都为 2。每个顶点的度数是通过计算连接到该特定顶点的边的数量来计算的。

对于图 1 中的顶点 A，有两条边与顶点 A 相关联，一条来自顶点 B，另一条来自顶点 D。因此，图一顶点 A 的度数为 2。类似地，对于图中的其他顶点，每个顶点只有两条边，顶点 B 和顶点 D。因此，顶点 B 和顶点 D 的度数都为 2。由于图中所有三个节点的度数都相同，即 2。因此，该图称为 2-正则图。

类似地，对于上面显示的第二个图，有四个顶点，分别称为顶点 E、顶点 F、顶点 G 和顶点 F。该图所有四个顶点的度数都为 2。图中的每个顶点都为 2，因为只有两条边与图中的所有顶点相关联。由于该图的所有节点都具有相同的度数 2，因此该图称为**正则图。

完全图

如果图中所有顶点之间都存在一条边，则称该图为完全图。换句话说，所有顶点都与其他所有顶点相连接。一个具有 'n' 个顶点的完全图包含恰好 nC2 条边，并且一个具有 'n' 个顶点的完全图表示为 Kn。

上面图像中显示了 K3 和 K4 两个图，它们都是完全图。图 K3 有三个顶点，每个顶点都至少与其余顶点有一条边相连。类似地，对于图 K4，有四个节点，分别称为顶点 E、顶点 F、顶点 G 和顶点 H。例如，顶点 F 连接了三条边，以便连接到图中的其余三个顶点。同样，对于其余三个顶点，每个顶点都有三条边与之关联。由于该图的所有顶点都有与其他顶点相连的独立边，因此它被称为**完全图。

圈图

如果一个有许多顶点（大于三个）和边的图形成一个圈，则该图称为**圈图。在圈状图中，所有顶点的度数都将为 2。

上面图像中显示了三个图，它们都是圈图的例子，因为所有这些图的节点数量都大于两个，并且所有这些图的所有顶点的度数都正好是 2。

有环图

一个图要被称为有环图，它应该至少包含一个圈。如果一个图至少存在一个圈，则称其为有环图。

图像中显示的图包含两个圈，满足图成为有环图的要求，因此它是一个有环图。

无环图

如果图不存在圈，则称该图为无环图，无环图是与有环图完全相反的概念。

上面图像中显示的图是无环的，因为它不存在圈。这意味着如果我们开始从顶点 B 遍历图，那么不存在一条路径可以遍历所有顶点并最终回到顶点 B。

有限图

如果一个图中存在的顶点数量和边数量都是有限的，则该图称为有限图。

上面图像中显示的图是有限图。有四个顶点，分别称为顶点 A、顶点 B、顶点 C 和顶点 D，并且该图中存在的边数量也是四个。由于该图中节点和顶点的数量都是有限的，因此称为有限图。

无限图

如果图中的顶点数量和边数量是无限的，也就是说图中的顶点和边无法计数，那么该图称为无限图。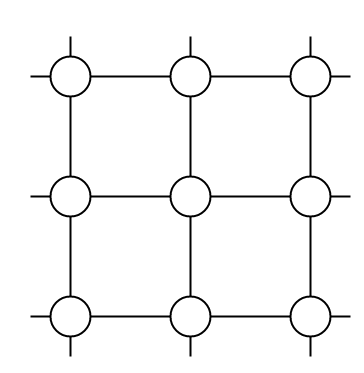

正如我们在上面图像中看到的，图中的顶点数量和边数量是无限的，所以这个图被称为无限图。

二分图

一个图要成为二分图，它需要满足一些基本前提条件。这些条件是：

• 图的所有顶点应该被划分为两个不同的顶点集 X 和 Y。
• 集合 X 中的所有顶点只能通过一些边连接到集合 Y 中的顶点。这意味着一个集合中的顶点不应该连接到同一个集合中的顶点。
• 创建的两个集合都应该是不同的，这意味着它们都不应该包含相同的顶点。

上面图像中显示的图被划分为两个顶点集，分别称为集 X 和集 Y。这些集合的内容是：

集合 X 的顶点 A 与集合 Y 的顶点 Q 相关联。顶点 B 也连接到顶点 Q。集合 X 的顶点 C 连接到集合 Y 的两个顶点，分别称为顶点 P 和顶点 R。集合 X 的顶点 D 与集合 R 的顶点 Q 相关联。

类似地，集合 Y 中的所有顶点都只连接到集合 X 中的顶点。并且集合 X 和集合 Y 都包含不重复或不同的元素。上面图像中显示的图满足了二分图的所有条件，因此它是一个二分图。

平面图

如果一个图可以在一个平面上绘制，并且任意两条边都不相交，则该图称为平面图。

上面图像中显示的图可以在一个平面上绘制，并且任意两条边都不相交。因此它是一个平面图。

简单图

如果一个图不包含自环和并行边，则该图称为简单图。

上面图像中显示的图有三个顶点和三条边。该图没有自环和并行边；因此，它被称为简单图。

多重图

如果一个图不包含自环，但包含并行边，则该图称为多重图。如果两个顶点之间存在多条边，则称这对顶点具有并行边。

上面图像中显示的图有三个顶点和三条边。没有自环，但有两条边连接了图中顶点 A 和顶点 E 之间的这两个顶点。换句话说，如果一个图的两个顶点被多条边连接，那么该图就被称为具有并行边，从而使其成为多重图。

伪图

如果一个图不包含并行边，但存在自环，则该图称为伪图。自环的含义是图中存在一条边，它从图的一个顶点开始，如果这条边在同一个顶点结束，那么它就被称为伪图。

上面图像中显示的图有顶点 A、顶点 B 和顶点 E。该图有四条边，其中三条边与顶点 A 相关联，在这三条边中，有一条是自环。在这四条边中没有并行边。由于上面显示的图具有自环且没有并行边，因此它是伪图。

欧拉图

如果图中的所有顶点都具有偶数度，则该图称为欧拉图。顶点的度数是指与顶点相关联的边数。因此，为了成为欧拉图，要求图中的所有顶点都与偶数条边相关联。

在上面图像中显示的图中，我们有五个顶点，分别称为顶点 A、顶点 B、顶点 C、顶点 D 和顶点 E。除了顶点 C 之外，所有顶点的度数都是 2，这意味着它们分别与两条边相关联。同时，顶点 C 与四条边相关联，使其度数为 4。顶点 C 和其他顶点的度数分别为 4 和 2，都是偶数。因此，上面显示的图是欧拉图。

哈密顿图

假设在连通图中存在一个闭合的行走的路径，该路径恰好访问图中的每个顶点一次（除了起始顶点），而不重复边。这样的图称为**哈密顿图**，这样的行走称为**哈密顿路径**。哈密顿回路也称为哈密顿圈。

换句话说，从同一顶点开始并结束于同一顶点的哈密顿路径称为哈密顿回路。包含哈密顿回路的每个图也包含哈密顿路径，但反之则不成立。图中可能存在多条哈密顿路径和哈密顿回路。

上面图像中显示的图包含一条闭合路径 ABCDEFA，该路径从顶点 A 开始，遍历所有其他顶点或节点，而不会在遍历路径中重复遍历除顶点 A 以外的任何节点。因此，上面图像中显示的图是哈密顿图。