最小堆和最大堆的区别

引言

在计算机科学中，堆是用于各种算法和应用程序的基本数据结构。堆的两种主要类型是最小堆和最大堆。虽然这两种结构相似，但它们执行的功能各不相同，并且根据排序方式的不同表现也不同。理解最小堆和最大堆之间的区别对于在编程工作中成功使用它们、优化算法和解决计算问题至关重要。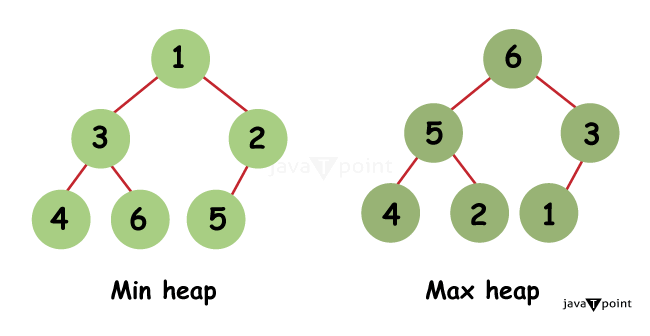

什么是最小堆？

最小堆是一种基于二叉树的数据结构，其中父节点的值小于或等于其子节点的值。最小元素始终位于根部，可以快速检索。它广泛应用于优先队列和需要快速访问最小元素的算法中。最小堆使得优先处理工作负载、在 Dijkstra 等算法中找出最短路径以及进行排序变得更加容易。它们的层次结构允许轻松地检测和操作即使是最小的值，这使得它们在需要高效处理优先数据的场景中非常重要。

关键特征

1. 根元素：堆的根部是最小的值。
2. 元素的排列方式：父节点的值小于或等于其子节点的值。
3. 插入操作：将新元素插入最小堆的过程包括将其放置在下一个可用位置。一旦满足堆的属性，该元素就会与其父节点交换，以恢复堆的属性。
4. 删除操作：在删除最小元素（根）后，堆中的最后一个元素被放置在根部。之后，直到满足堆的属性，新的根节点会与其最小的子节点交换，以恢复堆的属性。

让我们开发一个简单的最小堆示例

考虑以下数字集合：[10, 20, 15, 30, 40, 25, 35]。

为了将此集合表示为最小堆，我们首先创建一个二叉树。

• 在最小堆中，父节点的值必须小于或等于其后代的值。如上例所示，父节点的值小于其子节点，因此满足最小堆的条件。
• 然而，该二叉树仅部分符合最小堆的条件，因为包含 20 的节点大于其父节点 (10)。为了将此二叉树转换为最小堆，我们使用 heapify 函数。
• Heapify 涉及在树中向上或向下移动节点，以确保所有层都满足最小堆的属性。

应用 heapify 后，最小堆将如下所示：

现在每个父节点的值都小于其子节点，这满足了最小堆的条件。

什么是最大堆？

最大堆是一种特殊的二叉树结构，其中每个父节点的值大于或等于其子节点的值。最大值（最大值）存储在根部，可以轻松访问最大的元素。最大堆在需要快速检索或操作最大值的算法和应用程序中至关重要，例如工作调度和资源分配。它们通过使最重要的元素易于访问来促进优先排序和优化。最大堆用于各种需要识别和有效管理最大元素对于成功决策和系统性能至关重要的情况。

关键特征

1. 根元素：堆的最大值位于根部。
2. 元素的排列方式：父节点的值大于或等于其子节点的值。
3. 插入操作：将新元素添加到最大堆后，它会占据下一个可用位置。从那里开始，元素及其父节点会进行交换，直到满足堆的属性。
4. 删除操作：在删除最大元素（根）后，堆中的最后一个元素被放置在根部。之后，直到满足堆的属性，新的根节点会与其最大的子节点交换，以恢复堆的属性。

让我们用一个例子来解释最大堆

考虑以下数字集合：[30, 20, 25, 10, 15, 5, 35]。

为了将此集合表示为最大堆，我们首先创建一个二叉树。

• 在最大堆中，父节点的值必须大于或等于其后代的值。上述示例表明，父节点的值高于其后代，这表明了最大堆的属性。
• 然而，该二叉树仅部分符合最大堆的条件，因为包含 30 的节点小于其子节点 (35)。为了将此二叉树转换为最大堆，我们使用 heapify 函数。
• Heapify 涉及在树中向上或向下移动节点，以确保所有层都满足最大堆的属性。

应用 heapify 后，最大堆将如下所示：

现在，每个父节点的值都大于其子节点，这满足了最大堆的属性。

最小堆与最大堆的区别

结论

总而言之，最小堆和最大堆在组织和行为方式上有着根本的区别。最小堆确保最小元素位于根部，从而可以快速访问最小值。相比之下，最大堆将最大元素放在根部，从而可以快速检索最大值。它们的父节点连接、heapify 过程和遍历顺序使它们与众不同。最小堆非常适合需要优先队列和检索最小元素的应用。相比之下，最大堆在优先访问最大元素的情况下表现出色。这些特性使它们成为算法设计、资源分配和优化方面有用的工具，能够适应各个应用程序的需求。