AVL 树操作

2025年3月17日 | 阅读 15 分钟

1962 年，GM Adelson-Velsky 和 EM Landis 创建了 AVL 树。为了纪念创造者，这棵树被称为 AVL。

AVL 树的定义是高度平衡的二叉搜索树，其中每个节点都有一个平衡因子，该平衡因子是通过从左子树的高度中减去右子树的高度来确定的。

如果每个节点的平衡因子介于 -1 和 1 之间，则认为树是平衡的；否则，需要平衡树。

平衡因子

平衡因子 (k) = 高度 (左(k)) - 高度 (右(k))

如果任何节点的平衡因子为 1，则左子树比右子树高一个级别。
平衡因子为零的任何节点都表示左子树和右子树的高度相等。
如果节点的平衡因子为负一，则左子树比右子树低一个级别。
下图展示了一棵 AVL 树。我们可以看到每个节点的平衡因子都在 -1 到 +1 之间。因此，这是 AVL 树的一个例子。

为什么要使用 AVL 树？

大多数 BST 操作，包括搜索、最大值、最小值、插入、删除等，都需要 O(h) 时间，其中 h 是 BST 的高度。对于倾斜的二叉树，这些操作的成本可能会增加到 O(n)。如果我们确保在每次插入和删除后树的高度保持 O(log(n))，我们可以为所有这些操作提供 O(log(n)) 的上限。AVL 树的高度始终为 O(log(n))，其中 n 是树的节点数。

AVL 树上的操作

由于 AVL 树也是二叉搜索树，因此所有操作的执行方式与二叉搜索树中的操作相同。搜索和遍历不会导致 AVL 树属性的违反。然而，可能破坏此条件的动作是插入和删除；因此，需要对其进行审查。

插入
删除

AVL 树的插入

为了确保在每次插入后提供的树保持 AVL，我们必须在典型的 BST 插入过程中添加一些重新平衡。

以下两个简单的操作（keys(left) key(root) keys(right)) 可以在不违反 BST 属性的情况下用于平衡 BST。

左旋
右旋

The tree's T1, T2, and T3 subtrees are rooted with either y (on the left side) or x. (on the right side)
     y                                          x
    / \     Right Rotation          /  \
   x   T3   - - - - - - - >             T1    y 
  / \       < - - - - - - -                  / \
 T1  T2     Left Rotation        T2  T3
The order of the keys in the two trees mentioned above is as follows:
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
Therefore, no BST property has been broken.

插入的步骤如下

设 w 为新添加的节点。
对 w 执行典型的 BST 插入。
通过从 w 开始向上移动来找到第一个失衡节点。假设 z 是初始失衡节点，y 是 z 的子节点，位于从 w 到 z 的路径上，x 是 z 的孙节点，位于上述路径上。
以适当的方向旋转以 z 为根的子树以重新平衡树。由于 x、y 和 z 可以有 4 种不同的排序方式，因此可能有 4 种潜在的场景需要解决。
四种潜在的配置如下
- 左左情况：y 是 z 的左子节点，x 是 y 的左子节点。
- 左右情况：z 的右子节点和 x 的右子节点。
- 右右情况：y 是 z 的右子节点，x 是 y 的左子节点。
- 右右情况：y 是 z 的右子节点，x 是 y 的左子节点。

下面列出了在上述四种情况下要执行的过程。在每种情况下，我们只需要重新平衡以 z 为根的子树，并且一旦以 z 为根的子树的高度等于其插入前的值（通过适当的旋转），整个树就会平衡。

1. 左左情况

2. 左右情况

3. 右右情况

4. 右左情况

插入方法

概念是利用递归 BST 插入，在插入后，我们从底层获得指向每个祖先节点的指针。因此，不需要父节点指针就可以向上移动。递归代码本身会向上遍历并访问之前插入的每个节点。

为了将这个概念付诸实践，请遵循以下步骤：

执行标准的 BST 插入。
新插入节点的祖先必须是当前节点。应该更新当前节点的高度。
找到当前节点的平衡因子（左子树高度减去右子树高度）。
如果平衡因子大于 1，则当前节点不平衡，我们要么处于左左情况，要么处于左右情况。通过将新插入的键与左子树根节点处的键进行比较，可以确定是左左情况还是其他情况。

插入程序

// C program to insert a node in AVL tree
#include<stdio.h>
#include<stdlib.h>

// An AVL tree node
struct Node
{
	int key;
	struct Node *left;
	struct Node *right;
	int height;
};

// A utility function to get the height of the tree
int height(struct Node *N)
{
	if (N == NULL)
		return 0;
	return N->height;
}

// A utility function to get maximum of two integers
int max(int a, int b)
{
	return (a > b)? a : b;
}

/* Helper function that allocates a new node with the given key and
	NULL left and right pointers. */
struct Node* newNode(int key)
{
	struct Node* node = (struct Node*)
						malloc(sizeof(struct Node));
	node->key = key;
	node->left = NULL;
	node->right = NULL;
	node->height = 1; // new node is initially added at leaf
	return(node);
}

/ / A utility function to right rotate subtree rooted with y
// See the diagram given above.
struct Node *rightRotate(struct Node *y)
{
	struct Node *x = y->left;
	struct Node *T2 = x->right;

	// Perform rotation
	x->right = y;
	y->left = T2;

	// Update heights
	y->height = max(height(y->left),
					height(y->right)) + 1;
	x->height = max(height(x->left),
					height(x->right)) + 1;

	// Return new root
	return x;
}

// A utility function to left rotate subtree rooted with x
// See the diagram given above.
struct Node *leftRotate(struct Node *x)
{
	struct Node *y = x->right;
	struct Node *T2 = y->left;

	// Perform rotation
	y->left = x;
	x->right = T2;

	// Update heights
	x->height = max(height(x->left),
					height(x->right)) + 1;
	y->height = max(height(y->left),
					height(y->right)) + 1;

	// Return new root
	return y;
}

// Get Balance factor of node N
int getBalance(struct Node *N)
{
	if (N == NULL)
		return 0;
	return height(N->left) - height(N->right);
}

// Recursive function to insert a key in the subtree rooted
// with node and returns the new root of the subtree.
struct Node* insert(struct Node* node, int key)
{
	/* 1. Perform the normal BST insertion */
	if (node == NULL)
		return(newNode(key));

	if (key < node->key)
		node->left = insert(node->left, key);
	else if (key > node->key)
		node->right = insert(node->right, key);
	else // Equal keys are not allowed in BST
		return node;

	/* 2. Update height of this ancestor node */
	node->height = 1 + max(height(node->left),
						height(node->right));

	/* 3. Get the balance factor of this ancestor
		node to check whether this node became
		unbalanced */
	int balance = getBalance(node);

	// If this node becomes unbalanced, then
	// there are 4 cases

	// Left Left Case
	if (balance > 1 && key < node->left->key)
		return rightRotate(node);

	// Right Right Case
	if (balance < -1 && key > node->right->key)
		return leftRotate(node);

	// Left Right Case
	if (balance > 1 && key > node->left->key)
	{
		node->left = leftRotate(node->left);
		return rightRotate(node);
	}

	// Right Left Case
	if (balance < -1 && key < node->right->key)
	{
		node->right = rightRotate(node->right);
		return leftRotate(node);
	}

	/* return the (unchanged) node pointer */
	return node;
}

// A utility function to print preorder traversal
// of the tree.
// The function also prints height of every node
void preOrder(struct Node *root)
{
	if(root != NULL)
	{
		printf("%d ", root->key);
		preOrder(root->left);
		preOrder(root->right);
	}
}

/* Driver program to test above function*/
int main()
{
struct Node *root = NULL;

/* Constructing tree given in the above figure */
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 50);
root = insert(root, 25);

/* The constructed AVL Tree would be
	            30
		/ \
	          20 40
	     / \	 \
	    10 25   50
*/

printf("Preorder traversal of the constructed AVL"
		" tree is \n");
preOrder(root);
return 0;
}

输出

Preorder traversal of the constructed AVL tree is 
30 20 10 25 40 50
......................................................................................
Process executed in 1.22 seconds
Press any key to continue

说明

在旋转操作（左旋和右旋）期间，只更新了几个点，因此所需时间是常数。更新高度和获取平衡因子也需要恒定的时间。因此，AVL 插入的时间复杂度与 BST 插入相同，即 O(h)，其中 h 是树的高度。由于 AVL 树是平衡的 (Logn)，因此高度为 O。因此，AVL 插入的时间复杂度为 O(Logn)。

与红黑树的比较

红黑树

红黑树是一种自平衡二叉搜索树，其中每个节点都有一个额外的位，通常理解为颜色（红色或黑色）。通过使用这些颜色，可以在插入和删除期间保持树的平衡。尽管树的平衡不是完美的，但它足以减少搜索时间并将其保持在 O(log n) 或以下，其中 n 是树组件的总数。Rudolf Bayer 于 1972 年发明了这种树。

通过使用 AVL 树和其他自平衡搜索树（如红黑树），所有基本操作都可以在 O(log n) 时间内完成。与红黑树相比，AVL 树的分布更均匀，尽管在插入和删除期间可能会导致更多的旋转。因此，如果您的应用程序包含频繁的插入和删除操作，则建议使用红黑树。此外，如果搜索的频率更高，而插入和删除的频率较低，则应选择 AVL 树而不是红黑树。

AVL 树中的删除

在标准的 BST 删除过程中，我们必须添加一些重新平衡操作，以确保每次删除后，提供的树仍然是 AVL 树。以下两个简单的操作（keys(left) key(root) keys(right)) 可以在不违反 BST 属性的情况下用于重新平衡 BST。

左旋
右旋

树的 T1、T2 和 T3 子树由 y（在左侧）或 x（在右侧）根植。

上述两棵树中键的顺序如下：

keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)

令 w 为被删除的节点

对 w 执行标准的 BST 删除。
从 w 开始向上移动，找到第一个不平衡的节点。令 z 为第一个不平衡的节点，y 为 z 的较高高度的子节点，x 为 y 的较高高度的子节点。与插入不同，这里的 x 和 y 的定义发生了变化。
通过适当的方向旋转以 z 为根的子树来重新平衡树。由于 x、y 和 z 可以有 4 种不同的排序方式，因此可能有 4 种潜在情况需要处理。这四种潜在配置如下：
- 左左情况：y 是 z 的左子节点，x 是 y 的左子节点
- y 是 z 的左子节点，x 是 y 的右子节点。（左右情况）
- y 是 z 的右子节点，x 是 y 的右子节点。（右右情况）
- y 是 z 的右子节点，而 x 是 y 的左子节点。（右左情况）

与插入一样，上述 4 种情况下的执行步骤也相同。请注意，与插入不同，修复节点 z 可能无法完全修复 AVL 树。

1. 左左情况

2. 左右情况

3. 右右情况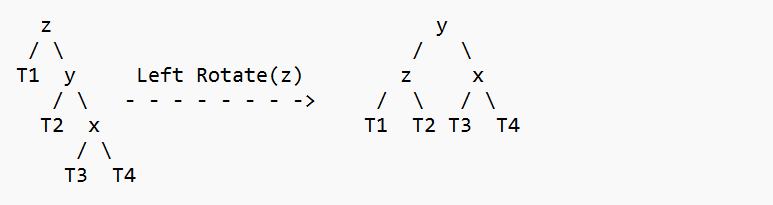

4. 右左情况

与插入不同，在删除操作中，在 z 处的旋转之后，可能需要在 z 的祖先处进行进一步的旋转。为了到达根节点，我们必须继续沿着路径前进。

删除方法

下面提供了 AVL 树的 C 语言删除实现。递归 BST 删除是以下 C 语言实现的基础。在递归 BST 删除期间，我们从底层逐个获得指向每个祖先节点的指针。因此，向上移动不需要父节点指针。递归代码本身会向上遍历并访问被删除节点的每个祖先。

执行标准的 BST 删除。
被删除节点的某个祖先必须是当前节点。应该更新当前节点的高度。
找到当前节点的平衡因子（左子树高度减去右子树高度）。
如果平衡因子大于 1，则当前节点不平衡，我们要么处于左左情况，要么处于左右情况。获取左子树的平衡因子以确定是左左情况还是左右情况。如果左子树的平衡因子大于或等于 0，则为左左情况；否则，为左右情况。
如果平衡因子小于 -1，则当前节点不平衡，我们要么处于右左情况，要么处于右右情况。获取右子树的平衡因子以确定是右右情况还是右左情况。如果右子树的平衡因子小于或等于 0，则为右右情况，否则为右左情况。

C 语言删除程序

// C program to delete a node from AVL Tree
#include<stdio.h>
#include<stdlib.h>
// An AVL tree node
struct Node
{
	int key;
	struct Node *left;
	struct Node *right;
	int height;
};

// A utility function to get maximum of two integers
int max(int a, int b);

// A utility function to get height of the tree
int height(struct Node *N)
{
	if (N == NULL)
		return 0;
	return N->height;
}

// A utility function to get maximum of two integers
int max(int a, int b)
{
	return (a > b)? a : b;
}

/* Helper function that allocates a new node with the given key and
	NULL left and right pointers. */
struct Node* newNode(int key)
{
	struct Node* node = (struct Node*)
						malloc(sizeof(struct Node));
	node->key = key;
	node->left = NULL;
	node->right = NULL;
	node->height = 1; // new node is initially added at leaf
	return(node);
}

// A utility function to right rotate subtree rooted with y
// See the diagram given above.
struct Node *rightRotate(struct Node *y)
{
	struct Node *x = y->left;
	struct Node *T2 = x->right;

	// Perform rotation
	x->right = y;
	y->left = T2;

	// Update heights
	y->height = max(height(y->left), height(y->right))+1;
	x->height = max(height(x->left), height(x->right))+1;

	// Return new root
	return x;
}

// A utility function to left rotate subtree rooted with x
// See the diagram given above.
struct Node *leftRotate(struct Node *x)
{
	struct Node *y = x->right;
	struct Node *T2 = y->left;

	// Perform rotation
	y->left = x;
	x->right = T2;

	// Update heights
	x->height = max(height(x->left), height(x->right))+1;
	y->height = max(height(y->left), height(y->right))+1;

	// Return new root
	return y;
}

// Get Balance factor of node N
int getBalance(struct Node *N)
{
	if (N == NULL)
		return 0;
	return height(N->left) - height(N->right);
}

struct Node* insert(struct Node* node, int key)
{
	/* 1. Perform the normal BST rotation */
	if (node == NULL)
		return(newNode(key));

	if (key < node->key)
		node->left = insert(node->left, key);
	else if (key > node->key)
		node->right = insert(node->right, key);
	else // Equal keys not allowed
		return node;

	/* 2. Update height of this ancestor node */
	node->height = 1 + max(height(node->left),
						height(node->right));

	/* 3. Get the balance factor of this ancestor
		node to check whether this node became
		unbalanced */
	int balance = getBalance(node);

	// If this node becomes unbalanced, then there are 4 cases

	// Left Left Case
	if (balance > 1 && key < node->left->key)
		return rightRotate(node);

	// Right Right Case
	if (balance < -1 && key > node->right->key)
		return leftRotate(node);

	// Left Right Case
	if (balance > 1 && key > node->left->key)
	{
		node->left = leftRotate(node->left);
		return rightRotate(node);
	}

	// Right Left Case
	if (balance < -1 && key < node->right->key)
	{
		node->right = rightRotate(node->right);
		return leftRotate(node);
	}

	/* return the (unchanged) node pointer */
	return node;
}

/* Given a non-empty binary search tree, return the
node with minimum key value found in that tree.
Note that the entire tree does not need to be
searched. */
struct Node * minValueNode(struct Node* node)
{
	struct Node* current = node;

	/* loop down to find the leftmost leaf */
	while (current->left != NULL)
		current = current->left;

	return current;
}

// Recursive function to delete a node with given key
// from subtree with given root. It returns root of
// the modified subtree.
struct Node* deleteNode(struct Node* root, int key)
{
	// STEP 1: PERFORM STANDARD BST DELETE

	if (root == NULL)
		return root;

	// If the key to be deleted is smaller than the
	// root's key, then it lies in left subtree
	if ( key < root->key )
		root->left = deleteNode(root->left, key);

	// If the key to be deleted is greater than the
	// root's key, then it lies in right subtree
	else if( key > root->key )
		root->right = deleteNode(root->right, key);

	// if key is same as root's key, then This is
	// the node to be deleted
	else
	{
		// node with only one child or no child
		if( (root->left == NULL) || (root->right == NULL) )
		{
			struct Node *temp = root->left ? root->left :
											root->right;

			// No child case
			if (temp == NULL)
			{
				temp = root;
				root = NULL;
			}
			else // One child case
			*root = *temp; // Copy the contents of
							// the non-empty child
			free(temp);
		}
		else
		{
			// node with two children: Get the inorder
			// successor (smallest in the right subtree)
			struct Node* temp = minValueNode(root->right);

			// Copy the inorder successor's data to this node
			root->key = temp->key;

			// Delete the inorder successor
			root->right = deleteNode(root->right, temp->key);
		}
	}

	// If the tree had only one node then return
	if (root == NULL)
	return root;

	// STEP 2: UPDATE HEIGHT OF THE CURRENT NODE
	root->height = 1 + max(height(root->left),
						height(root->right));

	// STEP 3: GET THE BALANCE FACTOR OF THIS NODE (to
	// check whether this node became unbalanced)
	int balance = getBalance(root);

	// If this node becomes unbalanced, then there are 4 cases

	// Left Left Case
	if (balance > 1 && getBalance(root->left) >= 0)
		return rightRotate(root);

	// Left Right Case
	if (balance > 1 && getBalance(root->left) < 0)
	{
		root->left = leftRotate(root->left);
		return rightRotate(root);
	}

	// Right Right Case
	if (balance < -1 && getBalance(root->right) <= 0)
		return leftRotate(root);

	// Right Left Case
	if (balance < -1 && getBalance(root->right) > 0)
	{
		root->right = rightRotate(root->right);
		return leftRotate(root);
	}

	return root;
}

// A utility function to print preorder traversal of
// the tree.
// The function also prints height of every node
void preOrder(struct Node *root)
{
	if(root != NULL)
	{
		printf("%d ", root->key);
		preOrder(root->left);
		preOrder(root->right);
	}
}

/* Driver program to test above function*/
int main()
{
struct Node *root = NULL;

/* Constructing tree given in the above figure */
	root = insert(root, 9);
	root = insert(root, 5);
	root = insert(root, 10);
	root = insert(root, 0);
	root = insert(root, 6);
	root = insert(root, 11);
	root = insert(root, -1);
	root = insert(root, 1);
	root = insert(root, 2);

	/* The constructed AVL Tree would be
			9
		/ \
		1 10
		/ \	 \
	0 5	 11
	/ / \
	-1 2 6
	*/

	printf("Preorder traversal of the constructed AVL "
		"tree is \n");
	preOrder(root);

	root = deleteNode(root, 10);

	/* The AVL Tree after deletion of 10
			1
		/ \
		0 9
		/	 / \
	-1 5	 11
		/ \
		2 6
	*/

	printf("\nPreorder traversal after deletion of 10 \n");
	preOrder(root);

	return 0;
}

输出

Preorder traversal of the constructed AVL tree is 
9 1 0 -1 5 2 6 10 11 
Preorder traversal after deletion of 10 
1 0 -1 9 5 2 6 11
.....................................................................................
Process executed in 2.11 seconds
Press any key to continue

说明

在旋转操作（左旋和右旋）期间，只更新了少量点，因此所需时间是恒定的。获取平衡因子和更新高度都需要时间。因此，AVL 删除的时间复杂度为 O(h)，其中 h 是树的高度，与 BST 删除相同。由于 AVL 树的平衡性 (Logn)，因此高度为 O。因此，AVL 删除的时间复杂度为 O。(Log n)。

AVL 树的优点

高度平衡是恒定的。
N 是节点数，高度永远不会超过 logN。
与二叉搜索树相比，它提供了更好的搜索性能。
它具有自平衡的能力。

总结

这些二叉搜索树是自平衡的。
平衡因子的值介于 -1 和 +1 之间。
当平衡因子超出范围时，必须进行旋转。
插入、删除和搜索的时间复杂度为 O。(log N)。
AVL 树通常用于搜索比插入和删除更频繁的场景。

下一主题数据结构中栈的局限性

AVL 树操作

平衡因子

为什么要使用 AVL 树？

AVL 树上的操作

AVL 树的插入

插入的步骤如下

插入方法

插入程序

与红黑树的比较

AVL 树中的删除

删除方法

C 语言删除程序

AVL 树的优点

总结

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

AVL 树操作

平衡因子

为什么要使用 AVL 树？

AVL 树上的操作

AVL 树的插入

插入的步骤如下

插入方法

插入程序

与红黑树的比较

AVL 树中的删除

删除方法

C 语言删除程序

AVL 树的优点

总结

相关帖子

最小交换次数将二叉树转换为二叉搜索树

内部排序和外部排序的区别

区间树

数据结构中的 K-D 树

二叉树的直径

最长公共子串

贪心算法的应用

移除链表中的循环

数据结构中的逆序对问题

哪个 Python 数据结构是不可变的

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器