满二叉树和完全二叉树的区别

什么是满二叉树？

满二叉树可以定义为一种 二叉树，其中所有节点都有 0 个或 2 个子节点。换句话说，满二叉树可以定义为一种二叉树，其中除叶节点外，所有节点都有两个子节点。

下面的树是满二叉树

上面的树是满二叉树，因为除叶节点外，所有节点都有两个子节点。

满二叉树定理

考虑一个非空二叉树 T

• 设 I 为树中的内部节点，L 为树中的叶节点，则叶节点数将等于
  L = I + 1
• 如果 T 有 I 个内部节点，N 为总节点数，则总节点数将等于
  N = 2I + 1
• 如果 T 包含 'N' 个总节点和 'I' 个内部节点，则内部节点数将等于
  I = (N-1)/2
• 如果 'T' 有 'N' 个总节点和 'L' 个叶节点，则叶节点数将等于
  L = (N+1)/2
• 如果 'T' 包含 'L' 个叶节点，则总节点数将等于
  N = 2L - 1
• 如果 'T' 有 'L' 个叶节点，'I' 为内部节点数，则内部节点数将等于
  I = L - 1

什么是完全二叉树？

当所有层都完全填满，除了最后一层从左侧开始填满时，二叉树被称为完全二叉树。

下面的树是完全二叉树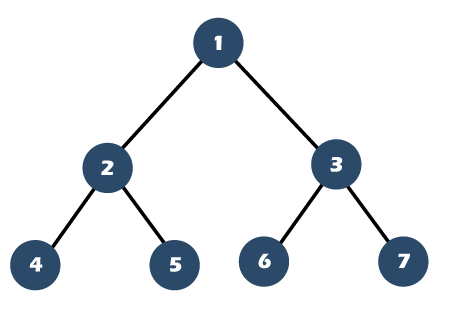

完全二叉树与满二叉树相似，除了以下两个区别

• 叶节点的填充必须从最左侧开始。
• 最后一个叶节点不强制要求有右兄弟节点。

让我们通过一个例子来理解上述几点

考虑下面的树

上面的树是一个完全二叉树，但不是一个满二叉树，因为节点 6 没有右兄弟节点。

完全二叉树的创建

假设我们有一个包含 6 个元素的数组，如下所示

上面的数组包含 6 个元素，即 1、2、3、4、5、6。以下是创建完全二叉树的步骤

步骤 1：首先，我们将选择数组的第一个元素，即 1，并将其作为树的根节点。第一层可用的元素数量是 1。

步骤 2：现在，我们将选择数组的第二个和第三个元素。将数组的第二个元素和第三个元素分别作为根节点的左子节点和右子节点，如下所示

如上所示，第二层可用的元素数量是 2。

步骤 3：现在，我们将从数组中选择接下来的两个元素，即 4 和 5。将这两个元素分别放在节点 2 的左侧和右侧，如下所示

如上所示，节点 4 和 5 分别是节点 2 的左子节点和右子节点。

步骤 4：现在，我们将选择数组的最后一个元素，即 6，并将其作为节点 3 的左子节点，因为我们知道在完全二叉树中，节点是从左侧开始填充的，如下所示

如我们所见，第二层包含 3 个元素。

让我们通过图片来理解完全二叉树和满二叉树之间的区别。

1. 下图所示的二叉树既不是完全二叉树也不是满二叉树。它不是满二叉树，因为节点 3 只有一个子节点。它也不是完全二叉树，因为节点应该从左侧开始填充，但节点 3 有一个右子节点而没有左子节点。
   
2. 下图所示的二叉树是满二叉树但不是完全二叉树。它是满二叉树，因为所有节点都有 0 个或 2 个子节点。它不是完全二叉树，因为节点 3 没有任何子节点，而节点 2 有其子节点，并且我们知道在完全二叉树中节点应该从左侧开始填充。
   
3. 下图所示的二叉树是完全二叉树但不是满二叉树。它是完全二叉树，因为所有节点都向左填充。它不是满二叉树，因为节点 2 只有一个子节点。
   
4. 下图所示的二叉树既是完全二叉树又是满二叉树。它是完全二叉树，因为所有节点都向左填充。它是满二叉树，因为所有节点都有 0 个或 2 个子节点。