数据结构中树的性质

2025年3月17日 | 阅读 7 分钟

引言

在二叉树中，这是一种由节点组成的层次数据结构，每个节点有两个子节点：左子节点和右子节点。树的最顶端节点称为根节点，作为遍历树的起点。没有子节点的节点称为叶子节点，而只有一个子节点的节点称为内部节点。二叉树中的每个节点的值都大于或等于其左子树中的值，并且小于或等于其右子树中的值。这种排序特性有助于对树进行高效的搜索、插入和删除操作。从根到叶子的最长路径的长度决定了树的深度，这用于确定节点的级别。二叉树的平衡因子对于保持效率很重要，因为平衡树确保高度始终相对于节点数呈对数关系。这些特性共同作用，提高了二叉树在各种环境中的适应性和效率，例如搜索算法、表达式解析和层次数据表示。

基本树概念

边和节点

节点和边的概念是任何树结构的基础。作为基本构建组件，将节点视为道路网络中的交叉点。每个节点都包含数据，并通过边连接到其他节点，从而形成树的分支。节点充当信息的存储空间，而边则显示这些存储空间之间的连接或链接。

内部节点、叶子节点和根节点

根

树的根节点是其顶点，是起点或最高节点。
它是所有其他节点的祖先，因为它没有父节点。

叶子

没有子节点的节点称为叶子节点或外部节点。
类似于自然界中树的叶子，它们位于分支的最末端。

内部节点

至少有一个非叶子节点的子节点的节点称为内部节点。
这些节点连接树的多个分支和层次，以构建内部框架。

父节点、子节点和兄弟节点

父子关系

父子关系连接树的节点。
具有一个或多个子节点的节点被视为父节点。
另一方面，具有父节点的节点是子节点。

兄弟姐妹

兄弟节点是具有相同父节点的节点。
这些连接在树中创建了家族层次结构，使得探索和理解结构化数据的表示方式变得更容易。

树的类型

计算机科学中有许多种树，每种都适合特定的需求和用途。为了有效解决问题和开发算法，理解这些不同树结构的属性和应用场景至关重要。

二叉树

二叉树本质上是一种数据结构，每个节点最多可以有两个子节点，通常称为左子节点和右子节点。对于更复杂的树数据结构，这种层次结构是证明。使用一个简单的 Python 函数，让我们探讨二叉树的起源。

代码

cl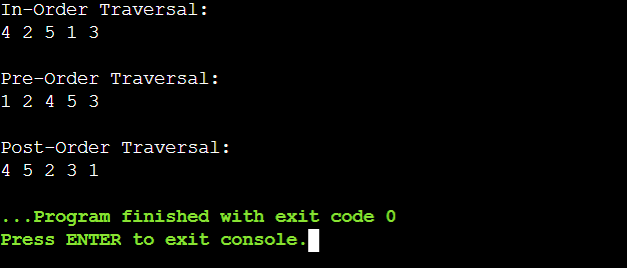ass Node:
    def __init__(self, key):
self.key = key
self.left = None
self.right = None
def in_order_traversal(node):
    if node:
in_order_traversal(node.left)
        print(node.key, end=" ")
in_order_traversal(node.right)
def pre_order_traversal(node):
    if node:
        print(node.key, end=" ")
pre_order_traversal(node.left)
pre_order_traversal(node.right)
def post_order_traversal(node):
    if node:
post_order_traversal(node.left)
post_order_traversal(node.right)
        print(node.key, end=" ")
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("In-Order Traversal:")
in_order_traversal(root)
print("\n")
print("Pre-Order Traversal:")
pre_order_traversal(root)
print("\n")
print("Post-Order Traversal:")
post_order_traversal(root)

输出

二叉搜索树（BST）

二叉树是一种序列类型，其中节点的左子树只包含键小于节点键的节点，右子树只包含键大于节点键的节点。这种特定类型的二叉树称为二叉搜索树（BST）。在 BST 中，搜索、插入和删除节点等操作是高效的。

代码

class Node:
    def __init__(self, key):
self.key = key
self.left = None
self.right = None
class BST:
    def __init__(self):
self.root = None
    def insert(self, key):
self.root = self._insert(self.root, key)
    def _insert(self, root, key):
        if not root:
            return Node(key)
        if key <root.key:
root.left = self._insert(root.left, key)
        else:
root.right = self._insert(root.right, key)
        return root
    def search(self, key):
        return self._search(self.root, key)
    def _search(self, root, key):
        if not root or root.key == key:
            return root
        if key <root.key:
            return self._search(root.left, key)
        return self._search(root.right, key)
    def in_order_traversal(self):
        result = []
        self._in_order_traversal(self.root, result)
        return result
    def _in_order_traversal(self, root, result):
        if root:
            self._in_order_traversal(root.left, result)
result.append(root.key)
            self._in_order_traversal(root.right, result)
bst = BST()
keys = [50, 30, 70, 20, 40, 60, 80]
for key in keys:
bst.insert(key)
search_result = bst.search(40)
print("Key 40 found in BST:", search_result is not None)
in_order_result = bst.in_order_traversal()
print("In-Order Traversal:", in_order_result)

输出

平衡 BST：AVL 树和红黑树

AVL 树：自平衡二叉搜索树

AVL 树是一种特殊的自平衡二叉搜索树。AVL 树中任意两个子树的高度差被限制为 1。如果在插入或删除操作的任何时候违反此属性，则会执行旋转以恢复平衡。

代码

class AVLNode:
    def __init__(self, key):
self.key = key
self.left = None
self.right = None
self.height = 1  
class AVLTree:
    def __init__(self):
self.root = None
    def _height(self, node):
        if not node:
            return 0
        return node.height
    def _update_height(self, node):
        if not node:
            return 0
node.height = 1 + max(self._height(node.left), self._height(node.right))
    def _balance_factor(self, node):
        if not node:
            return 0
        return self._height(node.left) - self._height(node.right)
    def _rotate_right(self, y):
        x = y.left
        T2 = x.right
x.right = y
y.left = T2
        self._update_height(y)
        self._update_height(x)
        return x
    def _rotate_left(self, x):
        y = x.right
        T2 = y.left
y.left = x
x.right = T2
        self._update_height(x)
        self._update_height(y)
        return y
    def _in_order_traversal(self, root, result):
        if root:
            self._in_order_traversal(root.left, result)
result.append(root.key)
            self._in_order_traversal(root.right, result)
    def in_order_traversal(self):
        result = []
        self._in_order_traversal(self.root, result)
        return result
    def insert(self, root, key):
        if not root:
            return AVLNode(key)
        if key <root.key:
root.left = self.insert(root.left, key)
        else:
root.right = self.insert(root.right, key)
        self._update_height(root)
        balance = self._balance_factor(root)
        if balance > 1 and key <root.left.key:
            return self._rotate_right(root)
        if balance < -1 and key >root.right.key:
            return self._rotate_left(root)
        if balance > 1 and key >root.left.key:
root.left = self._rotate_left(root.left)
            return self._rotate_right(root)
        if balance < -1 and key <root.right.key:
root.right = self._rotate_right(root.right)
            return self._rotate_left(root)
        return root
    def insert_key(self, key):
self.root = self.insert(self.root, key)
avl_tree = AVLTree()
keys = [50, 30, 70, 20, 40, 60, 80]
for key in keys:
avl_tree.insert_key(key)
in_order_result = avl_tree.in_order_traversal()
print("In-Order Traversal:", in_order_result)

输出

平衡二叉搜索树：红黑树

红黑树是另一种具有独特特性的自平衡二叉搜索树。这些特性保证了搜索、插入和删除操作的对数时间复杂度，同时确保树在插入和删除过程中保持平衡。

代码

class RBNode:
    def __init__(self, key, color):
self.key = key
self.left = None
self.right = None
self.color = color
class RedBlackTree:
    def __init__(self):
self.root = None
    def _left_rotate(self, node):
        y = node.right
node.right = y.left
y.left = node
        return y
    def _right_rotate(self, node):
        x = node.left
node.left = x.right
x.right = node
        return x
    def _flip_colors(self, node):
node.color = 'R'
node.left.color = 'B'
node.right.color = 'B'
    def _is_red(self, node):
        return node is not None and node.color == 'R'
    def _in_order_traversal(self, root, result):
        if root:
            self._in_order_traversal(root.left, result)
result.append(root.key)
            self._in_order_traversal(root.right, result)

    def in_order_traversal(self):
        result = []
        self._in_order_traversal(self.root, result)
        return result
    def insert(self, root, key):
        if not root:
            return RBNode(key, 'R')  
        if key <root.key:
root.left = self.insert(root.left, key)
elif key >root.key:
root.right = self.insert(root.right, key)
        if self._is_red(root.right) and not self._is_red(root.left):
            root = self._left_rotate(root)
        if self._is_red(root.left) and self._is_red(root.left.left):
            root = self._right_rotate(root)
        if self._is_red(root.left) and self._is_red(root.right):
            self._flip_colors(root)
        return root
    def insert_key(self, key):
self.root = self.insert(self.root, key)
self.root.color = 'B'  # Ensure the root is always black
rb_tree = RedBlackTree()
keys = [50, 30, 70, 20, 40, 60, 80]
for key in keys:
rb_tree.insert_key(key)
in_order_result = rb_tree.in_order_traversal()
print("In-Order Traversal:", in_order_result)

输出

N 叉树

N 叉树是一种树结构，其中每个节点可以有多个子节点。“N 叉”一词表示节点最多可以有“N”个子节点，其中“N”是表示此限制的变量。N 叉树提供比二叉树更灵活的结构，二叉树每个节点只允许有两个子节点。

代码

class NaryNode:
    def __init__(self, key):
self.key = key
self.children = []
class NaryTree:
    def __init__(self):
self.root = None
    def insert(self, parent_key, key):
        if not self.root:
self.root = NaryNode(key)
            return True
        return self._insert(self.root, parent_key, key)
    def _insert(self, node, parent_key, key):
        if not node:
            return False
        if node.key == parent_key:
node.children.append(NaryNode(key))
            return True

        for child in node.children:
            if self._insert(child, parent_key, key):
                return True
        return False
    def in_order_traversal(self, node, result):
        if not node:
            return
        for child in node.children:
self.in_order_traversal(child, result)
result.append(node.key)
    def display_tree(self):
        result = []
self.in_order_traversal(self.root, result)
        print("N-ary Tree:", result)
nary_tree = NaryTree()
nary_tree.insert(None, 1)  
nary_tree.insert(1, 2)     
nary_tree.insert(1, 3)     
nary_tree.insert(2, 4)     
nary_tree.insert(2, 5)     
nary_tree.insert(3, 6)     
nary_tree.display_tree()

输出

应用

文件系统：N 叉树经常用于建模文件系统。N 叉树结构非常适合目录，因为每个目录可以包含任意数量的文件或子目录。
组织结构图：N 叉树可以显示商业或教育环境中的组织层次结构。节点的直接下属由其子节点表示，可以是员工或部门。
抽象语法树 (AST)：AST 在编译器设计中描绘程序代码的层次结构。为了表示不同代码片段之间的连接，可以使用 N 叉树。
家谱：N 叉树是描绘家谱或族谱的常用方式。每个人都是一个节点，节点的后代是其后代的表示。
XML 和 HTML 文档结构：XML 和 HTML 页面的文档对象模型 (DOM) 通常表示为 N 叉树。XML 和 HTML 文档结构。文档的元素都是节点；嵌套元素是节点的子节点。

结论

树在计算工具箱中作为适应性强的工具出现，因为它们具有表达层次关系、有效搜索和检索数据以及适应专业应用程序的天然能力。树在众多领域中的普遍性强调了它们对计算机科学的重要性。树对于创建有效的算法和结构至关重要，无论是用于管理文件系统中的层次关系、使用哈夫曼树压缩数据还是优化搜索过程。树也是计算机科学中必不可少的构建块，由于它们对各种应用程序的适应性以及在保持最佳性能平衡方面的作用，它们为高效有效的问题解决铺平了道路。

下一主题归并排序的递推关系

← 上一个下一个 →

数据结构中树的性质

引言

基本树概念

边和节点

内部节点、叶子节点和根节点

父节点、子节点和兄弟节点

树的类型

二叉树

二叉搜索树（BST）

平衡 BST：AVL 树和红黑树

N 叉树

应用

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

数据结构中树的性质

引言

基本树概念

边和节点

内部节点、叶子节点和根节点

父节点、子节点和兄弟节点

树的类型

二叉树

二叉搜索树（BST）

平衡 BST：AVL 树和红黑树

N 叉树

应用

结论

相关帖子

生成两个数组的最大数

Golang 中的 AVL 树实现

查找二叉搜索树中的第 k 小元素

Karger 算法用于最小割

使用 RMQ 在二叉树中查找 LCA

Strassen 矩阵乘法

在 C++ 中查找给定布尔矩阵中具有最大公共区域大小的区域

股票收益问题

数据结构中的 Patricia Trie

复杂数据结构

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器