B 树可视化

在下面的教程中，我们将学习 B 树数据结构，并考虑对其进行可视化。

那么，让我们开始吧。

什么是 B 树？

B 树是一种特殊的 M 路搜索树，通常称为M 路树，它可以自行平衡。由于其平衡的结构，这些树通常用于操作和管理海量数据库并简化搜索。在 B 树中，每个节点最多可以有 n 个子节点。B 树是数据库管理系统 (DBMS) 中多级索引的示例。叶节点和内部节点都将具有记录引用。B 树被称为平衡存储树，因为所有叶节点都处于同一级别。

下图是 B 树的示例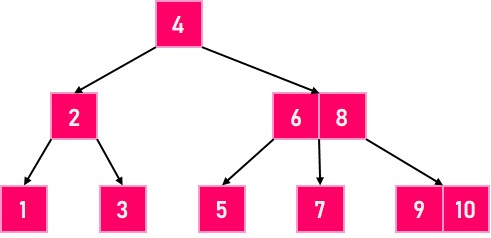

图 1。阶数为 3 的 B 树

理解 B 树的规则

以下是 B 树的重要属性

1. 所有叶节点都处于同一级别。
2. B 树数据结构由最小度数“d”定义。d 的值取决于磁盘块的大小。
3. 每个节点（根节点除外）必须至少包含 d-1 个键。根节点可以至少包含 1 个键。
4. 所有节点（包括根节点）最多可以包含 (2d-1) 个键。
5. 节点的孩子数量等于其包含的键的数量加上。
6. 节点的所有键均按升序排序。两个键 k1 和 k2 之间的子节点包含介于 k1 和 k2 之间的所有键。
7. 与二叉搜索树不同，B 树数据结构从根节点开始增长和收缩。而二叉搜索树从下往上生长和收缩。
8. 与其他的自平衡二叉搜索树一样，B 树数据结构在搜索、插入和删除等操作上的时间复杂度为 O(log?n)。
9. 节点插入 B 树仅发生在叶节点。

让我们看一个最小阶为 5 的 B 树的以下示例。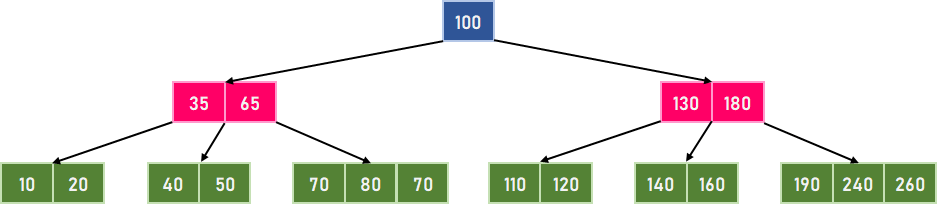

图 2。阶数为 5 的 B 树

注意：在实际的 B 树中，最小阶的值远大于 5。

在上图中，我们可以观察到所有叶节点都处于同一级别，并且所有非叶节点都没有空子树，并且包含的键比其子节点数少一。

B 树规则的集合表示

每个 B 树都依赖于一个正整数常量，称为 MINIMUM，它用于确定单个节点可以保存的数据元素的数量。

规则 1：根节点最少可以包含一个数据元素（如果它也没有子节点，则甚至可以不包含数据元素）；其他每个节点至少包含 MINIMUM 个数据元素。

规则 2：节点中存储的数据元素的最大数量是 MINIMUM 的两倍。

规则 3：B 树的每个节点的数据元素存储在一个部分填充的数组中，从最小数据元素（索引 0 处）到数组的最后一个已用位置（最大数据元素）排序。

规则 4：非叶节点下方的子树总数比该节点中的数据元素数量多一个。

• subtree 0,subtree 1,...

规则 5：对于任何非叶节点

1. 索引处的数据元素大于节点 i 号子树中的所有数据元素，并且
2. 索引处的数据元素小于节点 i+1 号子树中的所有数据元素。

规则 6：B 树中的每个叶节点都具有相同的深度。因此，它确保 B 树可以防止树不平衡的问题。

B 树数据结构的操作

为了确保在操作过程中 B 树数据结构的任何属性都不会被违反，B 树可以被分裂或合并。以下是我们可以在 B 树上执行的一些操作

1. 在 B 树中搜索数据元素
2. 在 B 树中插入数据元素
3. 在 B 树中删除数据元素

B 树上的搜索操作

在 B 树中搜索元素与在二叉搜索树中搜索元素类似。但是，B 树不是像二叉搜索树那样做出双向决策（左或右），而是在每个节点做出 M 路决策，其中 m 是该节点的子节点数量。

在 B 树中搜索数据元素的步骤

步骤 1：搜索从根节点开始。将搜索元素 k 与根节点进行比较。

步骤 1.1：如果根节点包含元素 k，则搜索完成。

步骤 1.2：如果元素 k 小于根节点中的第一个值，我们将移动到最左边的子节点，并递归地搜索该子节点。

步骤 1.3.1：如果根节点只有两个子节点，我们将移动到最右边的子节点，并递归地搜索子节点。

步骤 1.3.2：如果根节点有两个以上的键，我们将搜索剩余的。

步骤 2：如果在遍历整个树后未找到元素 k，则表示 B 树中不存在搜索元素。

让我们通过一个例子来可视化上述步骤。假设我们要搜索键 k=34 在以下 B 树中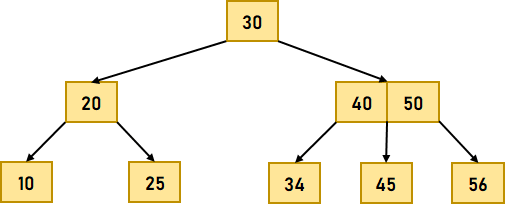

图 3.1。给定的 B 树

1. 首先，我们将检查键 k = 34 是否在根节点。由于根节点不包含该键，我们将转到其子节点。我们还可以观察到根节点有两个子节点；因此，我们将比较两个键之间的所需值。
   
   图 3.2。键 k 不在根节点
2. 现在我们可以看到键 k 大于根节点，即 30，我们将继续处理根节点的右子节点。
   
   图 3.3。键 k > 30，移动到右子节点
3. 我们现在将比较键 k 与节点中的值，即分别为 40 和 50。由于键 k 小于左键，即 40，我们将移动到节点的左子节点。
   
   图 3.4。键 k < 40，移动到左子节点
4. 由于 40 的左子节点中的值为 34，即所需值，我们可以得出结论，已找到键，搜索操作已完成。
   
   图 3.4。键 k = 34，40 的左子节点

在上面的例子中，我们比较了四个不同的值，直到找到它。因此，B 树中搜索操作所需的时间复杂度为 O(log?n)。

B 树上的插入操作

在向 B 树插入数据元素时，我们必须首先检查该元素是否已存在于树中。如果数据元素在 B 树中找到，则不会发生插入操作。但是，如果不是这种情况，我们将继续进行插入。在叶节点中插入元素时，需要考虑两种情况

1. 节点不包含超过 MAXIMUM 键数 -我们将把键插入到节点中的正确位置。
2. 节点包含 MAXIMUM 键数 -我们将把键插入到满节点，然后将发生分裂操作，将满节点分裂成三个部分。第二个或中键将移至父节点，第一部分和第三部分分别充当左子节点和右子节点。如果父节点也包含 MAXIMUM 键数，此过程将重复处理父节点。

在 B 树中插入数据元素的步骤

步骤 1：我们将首先根据 B 树的阶数计算节点中键的最大数量。

步骤 2：如果树为空，则分配根节点，我们将插入充当根节点的键。

步骤 3：我们现在将搜索适用于插入的节点。

步骤 4：如果节点已满

步骤 4.1：我们将按升序插入数据元素。

步骤 4.2：如果数据元素的数量超过了键的最大数量，我们将分裂满节点到中点。

步骤 4.3：我们将中键向上推，并将左部和右部键分裂为左子节点和右子节点。

步骤 5：如果节点未满，我们将按升序插入节点。

让我们通过一个例子来可视化上述步骤。假设我们需要创建一个阶数为 4 的 B 树。需要插入到 B 树的数据元素是 5,3,21,11,1,16,8,13,4,and 9。

1. 由于 m 等于 3，节点的最大键数 = m-1 = 3-1 = 2。
2. 我们将从在空树中插入 5 开始。
   
   图 4.1。插入 5
3. 我们现在将 3 插入到树中。由于 3 小于 5，我们将 3 插入到同一节点中 5 的左侧。
   
   图 4.2。插入 3
4. 我们现在将 21 插入到树中，由于 21 大于 5，它将被插入到同一节点中 5 的右侧。但是，我们知道节点中键的最大数量是 2，其中一个键将被移到一个上面的节点以进行分裂。因此，中间数据元素 5 将向上移动，3 和 21 分别成为其左子节点和右子节点。
   
   图 4.3。插入 21
5. 现在是时候插入下一个数据元素，即 11，它大于 5 但小于 21。因此，11 将作为键插入到包含 21 作为键的节点左侧。
   
   图 4.4。插入 11
6. 同样，我们将下一个数据元素 1 插入到树中，并且如我们所见，1 小于 3；因此，它将作为键插入到包含 3 作为键的节点左侧。
   
   图 4.5。插入 1
7. 现在，我们将数据元素 16 插入到树中，它大于 11 但小于 21。然而，该节点中的键数超过了键的最大数量。因此，节点将分裂，将中间的键移到根部。因此，16 将插入到 5 的右侧，将 11 和 21 分裂成两个单独的节点。
   
   图 4.6。插入 16
8. 数据元素 8 将作为键插入到 11 的左侧。
   
   图 4.7。插入 8
9. 我们将 13 插入到树中，它小于 16 且大于 11。因此，数据元素 13 应该插入到包含 8 和 11 的节点的右侧。但是，由于树中键的最大数量只能是 2，将发生分裂，将中间数据元素 11 移至上一个节点，并将 8 和 13 分成两个单独的节点。现在，上面的节点将包含 5、11 和 16，这再次超过了最大键数。因此，将发生另一次分裂，使数据元素 11 成为根节点，5 和 16 成为其子节点。
   
   图 4.8。插入 13
10. 由于数据元素 4 小于 5 但大于 3，它将被插入到包含 1 和 3 的节点的右侧，这将再次导致节点中的键数超过最大值。因此，将再次发生溢出，将 3 移至 5 旁边的上层节点。
    
    图 4.9。插入 4
11. 最后，数据元素 9，它大于 8 但小于 11，将被插入到包含 8 作为键的节点的右侧。
    
    图 4.10。插入 9

在上面的例子中，我们进行了不同的比较。第一个值直接插入到树中；之后，每个值都必须与树中可用的节点进行比较。B 树中插入操作的时间复杂度取决于节点的数量和 。

B 树上的删除操作

从 B 树中删除数据元素包含三个主要事件

1. 搜索要删除的键所在的节点，
2. 删除键，以及

• 如有必要，平衡树。

在从树中删除元素时，可能会发生称为“下溢”的条件。当一个节点包含的键数少于其应有的最小数量时，就会发生下溢。

以下是一些在可视化删除/移除操作之前需要理解的术语

1. 中序前驱：节点左子节点中最大的键称为其中序前驱。
2. 中序后继：节点右子节点中最小的键称为其中序后继。

以下是 B 树中删除操作的三个主要情况

情况 1：键的删除/移除位于叶节点 -此情况进一步分为两种不同的情况

1. 键的删除/移除不违反节点应有的最小键数属性。

让我们通过一个删除 B 树中键 32 的例子来可视化这种情况。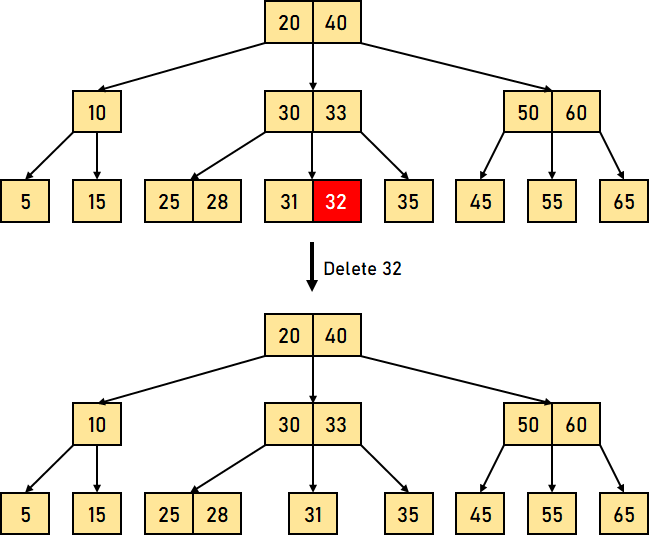

图 4.1：从 B 树中删除叶节点键 (32)

我们可以观察到，从该树中删除 32 并未违反上述属性。

2. 键的删除/移除违反了节点应有的最小键数属性。在这种情况下，我们必须从其相邻的同级节点借用一个键，按从左到右的顺序。

首先，我们将访问相邻的左同级节点。如果左同级节点具有的键数超过最小值，它将从该节点借用一个键。

否则，我们将尝试从相邻的右同级节点借用。

现在让我们通过一个删除上述 B 树中 31 的例子来可视化这种情况。在这种情况下，我们将从左同级节点借用一个键。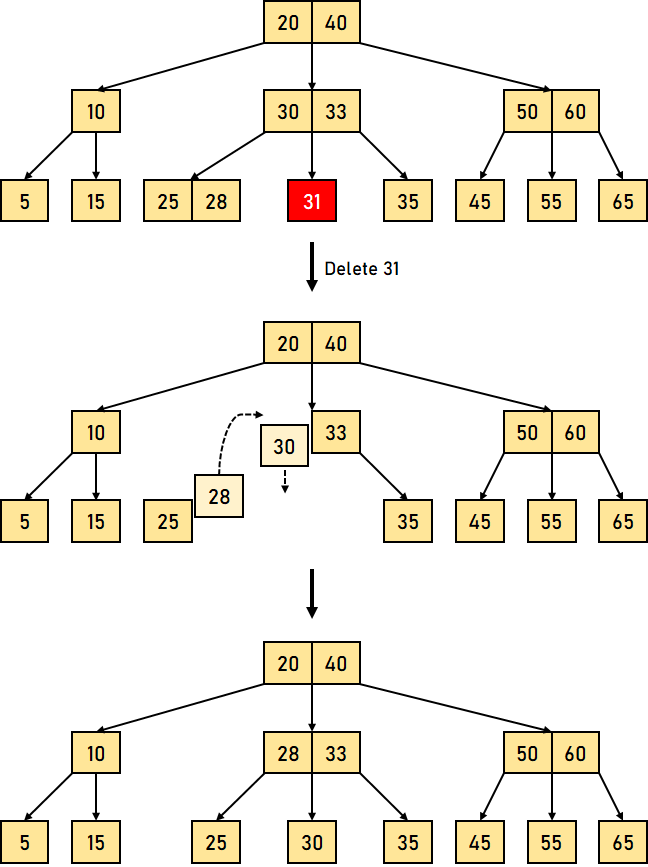

图 4.2：从 B 树中删除叶节点键 (31)

如果两个相邻的同级节点都已包含最小数量的键，那么我们将该节点与左同级节点或右同级节点合并。此合并过程通过父节点进行。

让我们通过删除上述 B 树中的键 30 来再次可视化。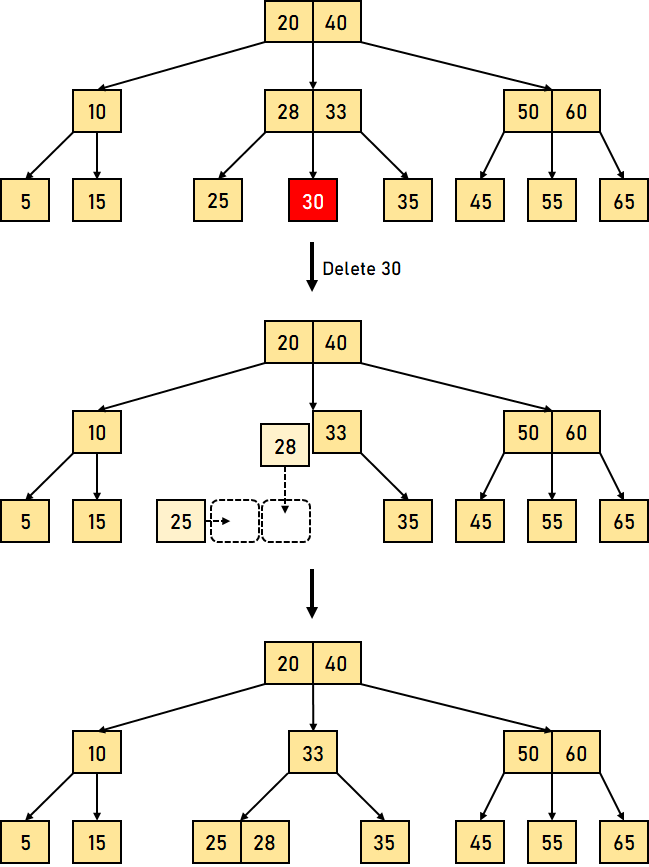

图 4.3：从 B 树中删除叶节点键 (30)

情况 2：要删除/移除的键位于非叶节点 -此情况进一步分为不同的情况

1. 如果左子节点中的键数超过最小值，则要删除的非叶/内部节点将被其中序前驱替换。

让我们通过删除 B 树中键 33 的例子来可视化这种情况。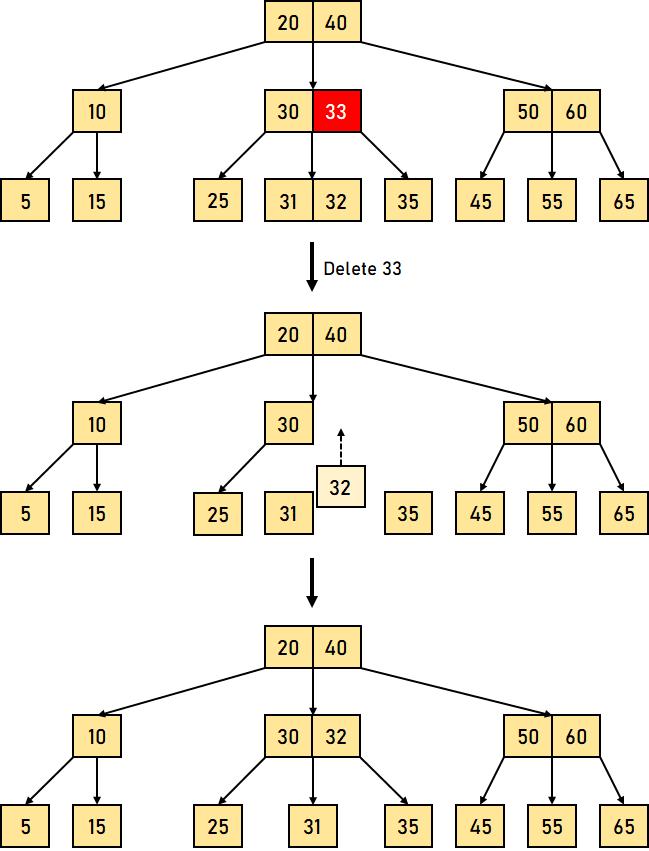

图 4.4：删除叶节点键 (33)（此处原文应为删除非叶节点键）

2. 如果右子节点中的键数超过最小值，则要删除的非叶/内部节点将被其中序后继替换。

如果任一子节点中的键数等于最小值，那么我们将合并左子节点和右子节点。

让我们通过删除 B 树中的键 30 来可视化这种情况。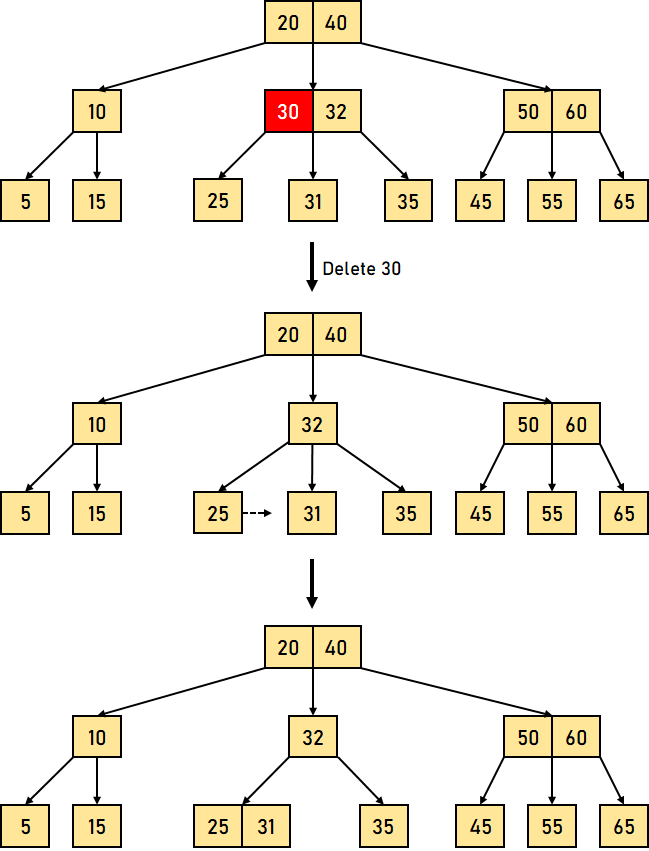

图 4.5：删除叶节点键 (30)（此处原文应为删除非叶节点键）

合并后，如果父节点中的键数少于最小值，则可以像情况 1 中那样查找同级节点。

情况 3：在这种情况下，树的高度缩小。如果目标键位于内部节点中，并且键的移除导致节点中的键数减少（少于必需的最小值），那么查找其中序前驱和中序后继。如果两个子节点都包含最小数量的键，则无法借用。这导致情况 2(3)，即合并子节点。

我们将再次查找同级节点以借用一个键。但是，如果同级节点也包含最小数量的键，那么我们将把该节点与同级节点以及父节点合并，并根据要求（升序）排列子节点。

让我们通过删除给定 B 树中的数据元素 10 的例子来可视化这种情况。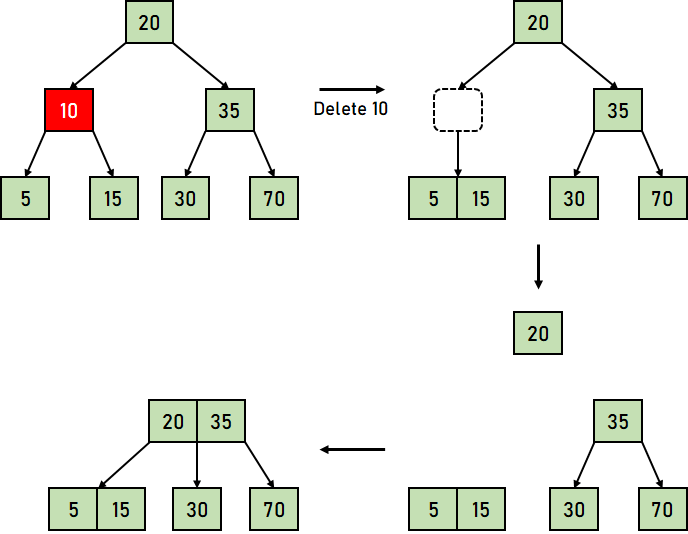

图 4.6：删除叶节点键 (10)（此处原文应为删除非叶节点键）

上述示例中的时间复杂度因需要从何处删除键而异。因此，B 树中删除操作的时间复杂度为 O(log?n)。

结论

在本教程中，我们学习了 B 树，并通过不同的示例对其各种操作进行了可视化。我们还理解了一些 B 树的基本属性和规则。