不相交集数据结构

Disjoint set data structure 也被称为 union-find data structure 和 merge-find set。它是一种包含不相交或不重叠集合的数据结构。Disjoint set 意味着当集合被划分为不相交的子集时。可以在不相交的子集上执行各种操作。在这种情况下，我们可以添加新集合，合并集合，还可以查找集合的代表成员。它还可以高效地查找两个元素是否属于同一个集合。

Disjoint set 可以定义为两个集合之间没有共同元素的子集。让我们通过一个例子来理解 disjoint sets。

s1 = {1, 2, 3, 4}

s2 = {5, 6, 7, 8}

我们有两个名为 s1 和 s2 的子集。s1 子集包含元素 1、2、3、4，而 s2 包含元素 5、6、7、8。由于这两个集合之间没有共同元素，如果我们考虑这两个集合的交集，将得不到任何结果。这也称为 disjoint set，其中没有共同元素。现在问题出现了，我们如何在它们上面执行操作。我们只能执行两个操作，即 find 和 union。

在 find 操作的情况下，我们需要检查元素存在于哪个集合中。下面显示了两个名为 s1 和 s2 的集合。

假设我们要对这两个集合执行 union 操作。首先，我们必须检查我们要执行 union 操作的元素是否属于不同的集合或同一个集合。如果它们属于不同的集合，我们就可以执行 union 操作；否则，不行。例如，我们要对 4 和 8 执行 union 操作。由于 4 和 8 属于不同的集合，所以我们应用 union 操作。一旦执行了 union 操作，就会在 4 和 8 之间添加一条边，如下所示：

当应用 union 操作时，集合将表示为

s1Us2 = {1, 2, 3, 4, 5, 6, 7, 8}

假设我们在 1 和 5 之间添加一条边。现在最终的集合可以表示为

s3 = {1, 2, 3, 4, 5, 6, 7, 8}

如果我们考虑上述集合中的任何一个元素，那么所有元素都属于同一个集合；这意味着图中存在环。

如何检测图中的环？

我们将通过一个例子来理解这个概念。考虑下面的例子，使用 disjoint sets 来检测环。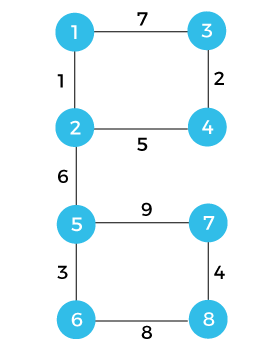

U = {1, 2, 3, 4, 5, 6, 7, 8}

每个顶点都标有某些权重。有一个包含 8 个顶点的通用集合。我们将逐个考虑每个边并形成集合。

首先，我们考虑顶点 1 和 2。它们都属于通用集合；我们对元素 1 和 2 执行 union 操作。我们将元素 1 和 2 添加到集合 s1 中，并从通用集合中删除这两个元素，如下所示：

s1 = {1, 2}

我们现在考虑的顶点是 3 和 4。这两个顶点都属于通用集合；我们对元素 3 和 4 执行 union 操作。我们将形成包含元素 3 和 4 的集合 s3，并从通用集合中删除这些元素，如下所示：

s2 = {3, 4}

我们现在考虑的顶点是 5 和 6。这两个顶点都属于通用集合，所以我们对元素 5 和 6 执行 union 操作。我们将形成包含元素 5 和 6 的集合 s3，并将这些元素从通用集合中删除，如下所示：

s3 = {5, 6}

我们现在考虑的顶点是 7 和 8。这两个顶点都属于通用集合，所以我们对元素 7 和 8 执行 union 操作。我们将形成包含元素 7 和 8 的集合 s4，并将这些元素从通用集合中删除，如下所示：

s4 = {7, 8}

下一个边是 (2, 4)。顶点 2 在集合 1 中，顶点 4 在集合 2 中，所以这两个顶点都属于不同的集合。当我们应用 union 操作时，它将形成新的集合，如下所示：

s5 = {1, 2, 3, 4}

下一个我们考虑的边是 (2, 5)。顶点 2 在集合 5 中，顶点 5 在集合 s3 中，所以这两个顶点都属于不同的集合。当我们应用 union 操作时，它将形成新的集合，如下所示：

s6 = {1, 2, 3, 4, 5, 6}

现在剩下两个集合，如下所示：

s4 = {7, 8}

s6 = {1, 2, 3, 4, 5, 6}

下一个边是 (1, 3)。由于这两个顶点，即 1 和 3 都属于同一个集合，因此它形成了一个环。我们不会考虑这个顶点。

下一个边是 (6, 8)。由于顶点 6 和 8 都属于不同的顶点 s4 和 s6，我们将执行 union 操作。union 操作将形成新的集合，如下所示：

s7 = {1, 2, 3, 4, 5, 6, 7, 8}

最后一条边是 (5, 7)。由于两个顶点都属于同一个名为 s7 的集合，因此形成了一个环。

如何图形化地表示集合？

我们有一个通用集合，如下所示：

U = {1, 2, 3, 4, 5, 6, 7, 8}

我们将逐个考虑每条边进行图形化表示。

首先，我们考虑顶点 1 和 2，即 (1, 2)，并以图形方式表示，如下所示：

在上图中，顶点 1 是顶点 2 的父节点。

现在我们考虑顶点 3 和 4，即 (3, 4)，并以图形方式表示，如下所示：

在上图中，顶点 3 是顶点 4 的父节点。

考虑顶点 5 和 6，即 (5, 6)，并以图形方式表示，如下所示：

在上图中，顶点 5 是顶点 6 的父节点。

现在，我们考虑顶点 7 和 8，即 (7, 8)，并以图形方式表示，如下所示：

在上图中，顶点 7 是顶点 8 的父节点。

现在我们考虑边 (2, 4)。由于 2 和 4 属于不同的集合，所以我们需要执行 union 操作。在上例中，我们观察到 1 是顶点 2 的父节点，而顶点 3 是顶点 4 的父节点。当我们对两个集合 s1 和 s2 执行 union 操作时，1 顶点将成为顶点 3 的父节点，如下所示：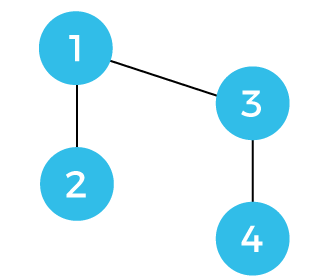

下一个边是 (2, 5)，权重为 6。由于 2 和 5 属于两个不同的集合，所以我们将执行 union 操作。我们将顶点 5 作为顶点 1 的子节点，如下所示：

我们选择顶点 5 作为顶点 1 的子节点，因为以顶点 1 为父节点的图的顶点数多于以顶点 5 为父节点的图。

下一个边是 (1, 3)，权重为 7。顶点 1 和 3 都属于同一个集合，所以不需要执行任何 union 操作。由于两个顶点都属于同一个集合；因此，存在一个环。我们已经检测到一个环，所以我们将继续考虑接下来的边。

如何通过数组检测环？

考虑下面的图

上图包含 8 个顶点。所以，我们将这 8 个顶点都表示在一个数组中。这里，索引代表 8 个顶点。每个索引都包含一个 -1 值。-1 值表示该顶点是自身的父节点。

现在我们将看到如何用数组表示集合。

首先，我们考虑边 (1, 2)。当我们用数组查找 1 时，我们观察到 1 是它自己的父节点。同样，顶点 2 是它自己的父节点，所以我们将顶点 2 作为顶点 1 的子节点。我们在索引 2 处添加 1，因为 2 是 1 的子节点。我们在索引 1 处添加 -2，其中 '-' 符号表示顶点 1 是它自己的父节点，2 表示集合中顶点的数量。

下一个边是 (3, 4)。当我们用数组查找 3 和 4 时；我们观察到这两个顶点都是它们自己的父节点。我们将顶点 4 作为顶点 3 的子节点，所以我们在数组的索引 4 处添加 3。我们在索引 3 处添加 -2，如下所示：

下一个边是 (5, 6)。当我们用数组查找 5 和 6 时；我们观察到这两个顶点都是它们自己的父节点。我们将 6 作为顶点 5 的子节点，所以我们在数组的索引 6 处添加 5。我们在索引 5 处添加 -2，如下所示：

下一个边是 (7, 8)。由于这两个顶点都是它们自己的父节点，所以我们将顶点 8 作为顶点 7 的子节点。我们在索引 8 处添加 7，并在数组的索引 7 处添加 -2，如下所示：

下一个边是 (2, 4)。顶点 2 的父节点是 1，顶点 4 的父节点是 3。由于这两个顶点具有不同的父节点，所以我们将顶点 3 作为顶点 1 的子节点。我们在索引 3 处添加 1。我们在索引 1 处添加 -4，因为它包含 4 个顶点。

图形化地，它可以表示为：

下一个边是 ( 2,5 )。当我们用数组查找顶点 2 时，我们观察到 1 是顶点 2 的父节点，并且顶点 1 是它自己的父节点。当我们用数组查找 5 时，我们发现 -2 值，这意味着顶点 5 是它自己的父节点。现在我们必须决定顶点 1 或顶点 5 哪个将成为父节点。由于顶点 1 的权重，即 -4 大于顶点 5 的权重，即 -2，所以当我们应用 union 操作时，顶点 5 将成为顶点 1 的子节点，如下所示：

在数组中，1 将被添加到索引 5，因为顶点 1 现在成为顶点 5 的父节点。我们在索引 1 处添加 -6，因为两个节点又被添加到节点 1。

下一个边是 (1,3)。当我们用数组查找顶点 1 时，我们观察到 1 是它自己的父节点。当我们用数组查找 3 时，我们观察到 1 是顶点 3 的父节点。因此，两个顶点的父节点相同；所以，我们可以说，如果我们包含边 (1,3)，则会形成一个环。

下一个边是 (6,8)。当我们用数组查找顶点 6 时，我们观察到顶点 5 是顶点 6 的父节点，而顶点 1 是顶点 5 的父节点。当我们用数组查找 8 时，我们观察到顶点 7 是顶点 8 的父节点，并且 7 是它自己的父节点。由于顶点 1 的权重，即 -6 大于顶点 7 的权重，即 -2，所以我们将顶点 7 作为子节点，并可以图形化地表示如下：

我们在索引 7 处添加 1，因为 7 成为顶点 1 的子节点。我们在索引 1 处添加 -8，因为图的权重现在变为 8。

要包含的最后一条边是 (5, 7)。当我们用数组查找顶点 5 时，我们观察到顶点 1 是顶点 5 的父节点。同样，当我们用数组查找顶点 7 时，我们观察到顶点 1 是顶点 7 的父节点。因此，我们可以说这两个顶点的父节点是相同的，即 1。这意味着包含边 (5,7) 会形成一个环。

到目前为止，我们已经学习了加权 union，其中我们根据顶点的权重执行 union 操作。权重较高的顶点成为父节点，权重较低的顶点成为子节点。使用此方法的缺点是，有些节点需要更多时间才能到达其父节点。例如，在上图中，如果我们想找到顶点 6 的父节点，顶点 5 是顶点 6 的父节点，所以我们移动到顶点 5，而顶点 1 是顶点 5 的父节点。为了克服这个问题，我们使用了“collapsing find”的概念。

collapsing find 技术是如何工作的？

考虑上面的例子。一旦我们知道顶点 6 的父节点是 1，我们就直接将顶点 6 添加到顶点 1。我们还将更新数组。在数组中，在索引 6 处添加 1，因为 6 的父节点现在是 1。直接将节点链接到集合的直接父节点的过程称为 collapsing find。类似地，我们可以将节点 8 和 4 链接到节点 1。