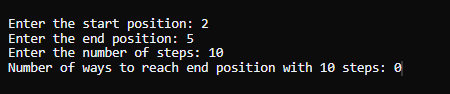
经过恰好 K 步到达某个位置的方法数

2025 年 2 月 9 日 | 阅读 9 分钟

问题陈述

在本问题陈述中，向我们提供了两个正整数 startPos 和 endPos。在一个无限的数轴上，我们从 startPos 位置开始。每一步我们可以向左移动一个位置，或者向右移动一个位置。

给定一个正整数 k，返回从 startPos 位置出发，在恰好 k 步内到达 endPos 位置的独立方法数。返回结果对 10^9 + 7 取模。

如果步行的顺序不同，则认为两种方法是不同的。

示例 1

输入: startPos = 1, endPos = 2, k = 3

输出 3

说明

步骤 1: 如果我们向右移动，我们将到达位置 2。所以，第一步后，我们有两种选择

向右移动: 1 -> 2
向左移动: 不可能

步骤 2: 现在，如果我们再次向右移动，我们将到达位置 3，这超出了我们的目标位置。所以，在第二步中，我们只能向左移动。因此，第二步后，我们有两种选择

向左移动: 2 -> 1
向右移动: 不可能

步骤 3: 在第三步中，我们可以向左或向右移动。两者都将我们带到位置 2。所以，第三步后，我们有两种选择

向左移动: 1 -> 2
向右移动: 1 -> 2

我们有 3 种不同的方法可以在恰好 3 步内从位置 1 到达位置 2。

1 -> 2 -> 3 -> 2

1 -> 2 -> 1 -> 2

1 -> 0 -> 1 -> 2

因此，输出是 3。

示例 2

输入: startPos = 2, endPos = 5, k = 10

输出 0

说明

步骤 1: 我们需要向右移动才能到达位置 3。

向右移动: 2 -> 3
向左移动: 不可能。

步骤 2: 现在，从位置 3 开始，我们可以向左或向右移动。

向左移动: 3 -> 2
向右移动: 3 -> 4

步骤 3-10: 对于接下来的 8 步，我们需要考虑所有可能的步骤。但是，考虑到所需步数（10），从位置 2 开始，在恰好 10 步内是不可能到达位置 5 的。

我们已经走了两步才能从位置 2 到达位置 3。
从位置 3 到位置 5 的最短路径是向右走两步（一步到位置 4，再一步到位置 5）。
走两步后，我们可能在位置 3，并且到达位置 5 需要至少再走两步。在前两步之后，只剩下八步，因此在恰好十步内是不可能到达位置 5 的。因此，输出为零。

示例 3

输入: startPos = 0 ,endPos = 4 ,k = 4

输出 4

说明

步骤 1: 我们需要向右移动才能到达位置 1。

向右移动: 0 -> 1
向左移动: 不可能

步骤 2: 从位置 1 开始，我们可以向左或向右移动。

向左移动: 1 -> 0
向右移动: 1 -> 2

步骤 3: 现在，从位置 0 开始，我们有两种选择

向右移动: 0 -> 1 -> 2
向左移动: 0 -> -1 -> 0

步骤 4: 在最后一步中，我们可以从位置 2 向左或向右移动，以到达位置 4。

向右移动: 2 -> 3 -> 4
向左移动: 2 -> 1 -> 2 -> 3 -> 4

因此，总共有 4 种不同的方法可以在恰好 4 步内从位置 0 到达位置 4。

0 -> 1 -> 2 -> 3 -> 4

0 -> -1 -> 0 -> 1 -> 2 -> 3 -> 4

0 -> 1 -> 2 -> 1 -> 2 -> 3 -> 4

0 -> -1 -> 0 -> 1 -> 2 -> 3 -> 4

因此，输出是 4。

Java 动态规划方法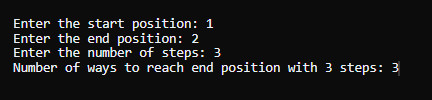

import java. util.Scanner; 
public class Solution {
        public int numberOfWays(int startPos, int endPos, int k) {
        // Modulo value for calculations
        int mod = 1000000007;
int[][] dp = new int[3002][k + 1];
        // Initialization: Set the starting position with k steps remaining to 1 way
dp[startPos + 1000][k] = 1;
        // Dynamic programming for different remaining steps
        for (int stepsLeft = k - 1; stepsLeft >= 0; stepsLeft--) {
            // Iterate over different positions
            for (int idx = 1; idx <= 3000; idx++) { 
// Calculate the number of ways to reach a current position from the previous or next position
dp[idx][stepsLeft] = ((dp[idx][stepsLeft] + dp[idx - 1][stepsLeft + 1]) % mod + dp[idx + 1][stepsLeft + 1]) % mod;
            }
        }
        // Return the number of ways to reach endPos 
        return dp[endPos + 1000][0];
    }
    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
        
System.out.println("Enter the start position:");
        int startPos = scanner.nextInt();
System.out.println("Enter the end position:");
        int endPos = scanner.nextInt();
System.out.println("Enter the number of steps:");
        int k = scanner.nextInt();
scanner.close();
        
Solution solution = new Solution();
        // Call the numberOfWays function and print the result
        int ways = solution.numberOfWays(startPos, endPos, k); 
System.out.println("Number of ways to reach end position with " + k + " steps: " + ways);
    }
}

输出

Number of Ways to Reach a Position after Exactly K Steps

代码解释

初始化

为了处理模运算，请将变量初始化为模值 1000000007 (10^9+7)。

动态规划数组 (dp): 创建一个大小为 [3002][k + 1] 的二维数组，用于存储到达每个位置所剩步数的选项数量。

初始化起始位置

起始位置 (startPos): 将 dp[startPos + 1000][k] 设置为 1，表示以 k 步到达起始位置的一种方式。

动态规划循环

外层循环 (stepsLeft) 从 k - 1 迭代到 0，表示每次移动后剩余的步数。

内层循环 (idx) 迭代位置从 1 到 3000，表示所有潜在的可能结果。

要更新 dp 数组，请将到达 idx 从前一个位置 (idx - 1) 和下一个位置 (idx + 1) 的方法数相加。为避免整数溢出，请确保结果已取模。

返回结果

最终结果: 返回到达 endPos 且剩余步数为 0 的方法数。从 dp[endPos + 1000][0] 中检索此值。

时间复杂度

该算法的时间复杂度为 O(K*3000)，其中 k 是步数，3000 是可能的最大位置数。该算法很复杂，因为每次移动都需要执行步进计算以获得每个可能的位置。

空间复杂度

空间复杂度也为 O(k * 3000)，因为它使用了一个大小为 3002 * (k + 1) 的二维数组来保存通过剩余步数到达每个位置的方法数。在这种情况下，空间在逻辑上会随着步数和位置的数量呈线性增长。

Java 使用记忆化的方法

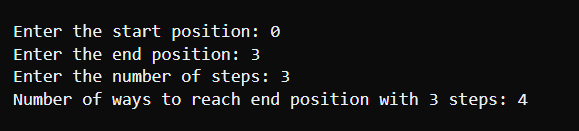
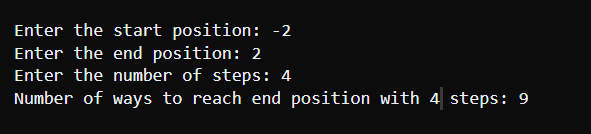import java.util.Scanner;
public class Solution {
 int mod = 1000000007; 
    int util(int s, int e, int curr, int k, int[][] dp){
        if(k == 0){
            if(curr == e) return 1;
            return 0;
        }
        if(dp[curr + 1001][k] != -1){
            return dp[curr + 1001][k];}
        int a = util(s, e, curr + 1, k - 1, dp) % mod;
        int b = util(s, e, curr - 1, k - 1, dp) % mod;
                return dp[curr + 1001][k] = (a + b) % mod; 
    }
    public int numberOfWays(int s, int e, int k) {
        int[][] dp = new int[3002][1001];
        for(int[] item : dp){
            Arrays.fill(item, -1);
        }
        return util(s, e, s, k, dp);
    }    public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
        // Input the start position, end position, and number of steps
System.out.println("Enter the start position:");
        int startPos = scanner.nextInt();
System.out.println("Enter the end position:");
        int endPos = scanner.nextInt();
System.out.println("Enter the number of steps:");
        int k = scanner.nextInt();
scanner.close();
        // Create an instance of the Solution class
Solution solution = new Solution();
        // Call the numberOfWays function and print the result
        int ways = solution.numberOfWays(startPos, endPos, k); 
System.out.println("Number of ways to reach end position with " + k + " steps: " + ways);
    }
}

输出

代码解释

初始化

该算法将模值初始化为 1000000007，以防止计算过程中发生整数溢出。它还定义了一个大小为 [3002][1001] 的记忆化数组 dp，用于存储子问题的结果。
选择 3002 作为大小是为了容纳从 -1000 到 1000（含）的位置，而 1001 代表允许的最大步数。该数组的初始值是 -1，表示尚未解决相关的子问题。

辅助函数 (util)

如果不再有剩余步数 (k == 0)，请验证当前位置是否为目标位置 (curr == e)。如果是，则函数返回 1（表示有一条有效路径），否则返回 0，表示没有有效路径。
如果当前位置和剩余步数的结果已经计算过（存储在 dp[curr + 1001][k] 中），则返回存储的结果。
该程序通过向前迈一步 (curr + 1) 和向后迈一步 (curr - 1) 来递归确定到达目标位置的方法数。它使用记忆化来存储和检索中间结果，从而避免不必要的计算。
最后，结果将存储在 dp[curr + 1001][k] 中并返回。

时间复杂度

作为解决方案，时间复杂度为 O(k*n)，其中 k 和 n 分别代表步数和最大可能集合的大小。原因是回溯算法能够通过动态规划尝试每种可能的步数和位置组合。

空间复杂度

因此，空间复杂度也为 O(k * n)。这是因为使用了大小为 (3002, 1001) 的二维表，其中位置数（3002）和步数（1001）存储了通过步数到达某个位置的方法数。

Java 使用递归的方法

import java. util.Scanner; 
public class Solution {
    // Function to find the number of ways to reach position 'e' from position 's' in 'k' steps
    public int numberOfWays(int s, int e, int k) {
        // Call the helper function to find the number of ways
        return find(s, e, k);
    }
    // Helper function to recursively find the number of ways
    public int find(int s, int e, int k) {
        // Base case: If no steps are left, return 1 if the current position is equal to the target position, else return 0
        if (k == 0) {
            if (s == e) return 1; 
return 0;
        }
        // Recursive calls: Try moving one step forward and one step backward
        int a = find(s + 1, e, k - 1);
        int b = find(s - 1, e, k - 1); 
        // Return the sum of ways obtained from moving forward and backward
        return a + b;
    }
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        // Input the start position, end position, and number of steps
System.out.println("Enter the start position:");
        int startPos = scanner.nextInt();
System.out.println("Enter the end position:");
        int endPos = scanner.nextInt();
System.out.println("Enter the number of steps:");
        int k = scanner.nextInt();
scanner.close();
        // Create an instance of the Solution class
Solution solution = new Solution();
        // Call the numberOfWays function and print the result
        int ways = solution.numberOfWays(startPos, endPos, k); 
System.out.println("Number of ways to reach end position with " + k + " steps: " + ways);
    }
}

输出

代码解释

numberOfWays 方法

计算的起点是此方法。需要三个参数: 步数 (k)、起始位置 (s) 和结束位置 (e)。
它将实际计算分配给 find 辅助函数。
numberOfWays 直接返回 find 返回的结果。

find 辅助函数

此函数应用递归来计算从起始点 (s) 到结束点 (e) 在给定的剩余步数 (k) 内可以行进的方法数。
基本情况: 如果 k == 0，则可能 s == e。如果相等，则返回 1，表示存在一条有效路径；否则返回 0，表示未找到有效路径。
递归调用: 如果还有要走的步数 (k > 0)，则该函数在递归级别上调用该函数两次。
第二步将设计为代表向前一步 (s + 1)，只剩下 k - 1 步。
第二次代表向后退一步 (s - 1)，只剩下 k - 1 步。
组合结果: 它将向前和向后移动时获得的结果相加，以计算从当前位置在 k 步内到达目的地的所有方法数。

时间复杂度

此问题需要 O(2k) 的时间复杂度，其中 'k' 是步数。这可以与递归函数在每个节点上做出两个选择，从而导致二叉递归调用结构的结果相关联。

空间复杂度

该解决方案的空间复杂度也为指数级 O(2^K)，这是由递归调用和调用堆栈使用的空间引起的。此外，递归函数会产生一个调用堆栈，该堆栈的运行与步数相关，并引入了额外的、呈线性增长的空间复杂度。

下一个主题划分成 k 个等和子集

经过恰好 K 步到达某个位置的方法数

问题陈述

示例 1

说明

示例 2

说明

示例 3

说明

Java 动态规划方法

代码解释

时间复杂度

空间复杂度

Java 使用记忆化的方法

代码解释

时间复杂度

空间复杂度

Java 使用递归的方法

代码解释

时间复杂度

空间复杂度

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

经过恰好 K 步到达某个位置的方法数

问题陈述

示例 1

说明

示例 2

说明

示例 3

说明

Java 动态规划方法

代码解释

时间复杂度

空间复杂度

Java 使用记忆化的方法

代码解释

时间复杂度

空间复杂度

Java 使用递归的方法

代码解释

时间复杂度

空间复杂度

相关帖子

二叉迷宫中的最短路径

Trie 数据结构

矩阵的转换

布尔矩阵问题

给定数组 A[] 和数字 x，检查 A[] 中是否存在和为 x 的对 (也称为两数之和)

二叉树中最大的 BST

单调栈导论

查找满足方程 N = P^2.Q 的 P 和 Q 的值

数据结构中矩阵中回文路径的数量

二叉搜索树中的最低公共祖先

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器