使用队列实现栈

堆栈是一种遵循 LIFO（后进先出）原则的线性数据结构，这意味着最先插入的元素将最后被移除。另一方面，队列是一种遵循 FIFO（先进先出）原则的线性数据结构，这意味着最先添加的元素将最先被移除。现在，我们将讨论如何使用队列实现堆栈。

使用队列实现堆栈有两种方法

• 首先，我们可以使 push 操作开销大。
• 其次，我们可以使 pop 操作开销大。

第一种方法：使 push 操作开销大

让我们通过一个例子来理解。

假设我们有以下列表

1, 5, 3, P, 2, P

在上面的列表中，'P' 表示我们必须执行 pop 操作，而整数 1、5、3 和 2 则要插入堆栈中。我们将通过队列来实现。或者我们可以说，我们将通过队列来实现 push 和 pop 操作。

首先，我们创建两个空队列，如下所示

在上面，我们创建了两个队列，即 Queue1 和 Queue2。首先，我们将元素 1 推入 Queue1，因此 front 和 rear 都指向元素 1，如下所示

插入元素 1 后，我们必须将元素 5 插入 Queue1。首先，我们从 Queue1 中弹出元素 1 并将其推入 Queue2，然后我们将元素 5 推入 Queue1，如下所示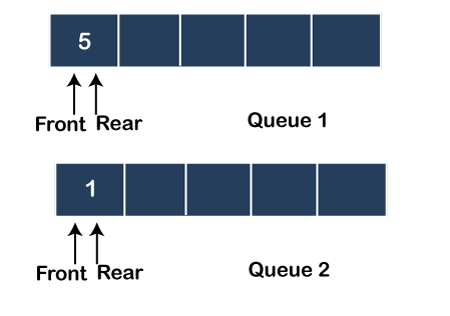

如上图所示，Queue1 中的 front 和 rear 都指向元素 5，而 Queue2 中的 front 和 rear 都指向元素 1。元素 5 插入完成后，Queue2 中的元素 1 返回到 Queue2。在 Queue1 中，front 将指向元素 5，rear 将指向元素 1，如下所示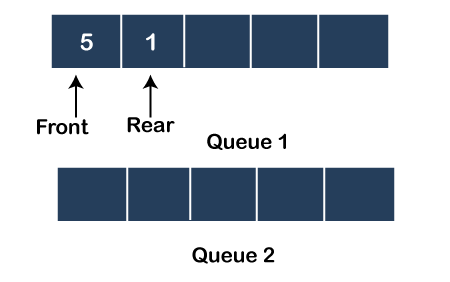

现在下一个元素是 3，我们必须将其插入 Queue1。为了实现这一点，Queue1 中的所有元素，即 5 和 1，都将被弹出并添加到 Queue2 中。

一旦元素从 Queue1 中弹出，元素 3 将被推入 Queue1，并且 front 将指向元素 3，如下所示

将元素 3 推入 Queue1 后，我们将从 Queue2 中弹出所有元素并将其推回 Queue1。front 将指向元素 3，rear 将指向元素 1，如下所示

下一个操作是 pop 操作。到目前为止，我们已经观察到 push 操作开销大，但 pop 操作需要 O(1) 时间。因此，我们将从 Queue1 中弹出元素 3 并更新 front 指针。弹出的元素将在输出中打印。现在 front 将指向元素 5，如下所示

要插入的下一个元素是 2。首先，我们将从 Queue1 中弹出所有元素并将其添加到 Queue2 中，如下所示

一旦所有元素都从 Queue1 中弹出，元素 2 将被推入 Queue1。Queue1 的 front 和 rear 将指向元素 2，如下所示

将元素插入 Queue1 后，我们将从 Queue2 中弹出所有元素并将其移回 Queue1，如下所示

如上图所示，front 指向元素 2，而 rear 指向元素 1。

下一个操作是 pop 操作。在 pop 操作中，元素 2 将从 Queue1 中弹出并在输出中打印。front 指针被更新并指向元素 5，如下所示

输出是 3, 2。

如果我们想验证输出是否正确，我们可以使用堆栈。首先，我们将元素 1 推入堆栈，如下所示

下一个元素 5 被推入堆栈，如下所示

下一个元素 3 将被推入堆栈，如下所示

现在将调用 pop 操作，元素 3 将从堆栈中弹出。元素 3 在输出中打印，如下所示

下一个要推入堆栈的元素是 2

插入 2 后，将调用 pop 操作，元素 2 将从堆栈中弹出。元素 2 在输出中打印。

输出是 3, 2，这与通过队列实现生成的输出相同。

时间复杂度

如果我们通过队列实现堆栈，那么 push 操作将需要 O(n) 时间，因为所有元素都需要从 Queue1 中弹出并推回 Queue1。

pop 操作将需要 O(1) 时间，因为我们需要从队列中移除前端元素。

算法（当 push 操作开销大时）

Push 算法

以下是执行 push 操作的步骤

步骤 1： 考虑两个队列，即 Q1 和 Q2，要插入队列的元素为 x。

步骤 2： 如果 Q1.isEmpty() 则

             Q1.enqueue(x);

             否则

             size:= Q1.size();

             对于 i=0…size 执行

             Q2.enqueue(Q1.dequeue());

             结束

             Q1.enqueue(x);

             对于 j=0….size 执行

             Q1.enqueue(Q2.dequeue());

             结束

Pop 算法

以下是执行 pop 操作的步骤

步骤 1： 考虑两个队列，即 Q1 和 Q2，我们想从队列的前端移除元素。

步骤 2： item:= Q1.dequeue();

步骤 3： 返回 item;

第二种方法：使 pop 操作开销大

假设我们有以下列表

1, 5, 3, P, 2, P

我们将考虑两个队列，即 Queue1 和 Queue2，正如我们在前一种方法中所做的那样。首先，我们将元素 1 推入 Queue1，如下所示

下一个元素是 5，它将被推入 Queue1，如下所示

下一个元素是 3，它也将被推入 Queue1，如下所示

现在我们必须在 Queue1 上执行 pop 操作。在这种情况下，我们将首先弹出除最后一个（由 rear 指向）之外的所有元素，并将它们添加到 Queue2 中。最后一个元素将从 Queue1 中移除并在输出中打印，如下所示

现在我们将 Queue2 的元素移回 Queue1。

下一个元素是 2，它将被插入 Queue1，如下所示

下一个操作是 pop 操作。在此操作中，首先，我们需要从 Queue1 中弹出除最后一个（由 rear 指向）之外的所有元素，并将其添加到 Queue2 中。最后一个元素，即 2，将从 Queue1 中移除并在输出中打印，如下所示

添加到 Queue2 中的元素将移回 Queue1，如下所示

如上图所示，生成的输出为 3, 2，队列中剩余的元素为 1, 5。

时间复杂度

在上述情况下，push 操作需要 O(1) 时间，因为在每次 push 操作中，新元素都添加到队列的末尾。另一方面，pop 操作需要 O(n) 时间，因为在每次 pop 操作中，除了最后一个元素外，所有元素都从 Queue1 中弹出并推入 Queue2。Queue1 中的最后一个元素将被删除，然后 Queue2 中的所有元素都移回 Queue1。

算法（当 pop 操作开销大时）

Push 算法

以下是执行 push 操作的步骤

步骤 1： 考虑两个队列，即 Q1 和 Q2，要插入队列的元素为 x。

步骤 2： element= Q1.enqueue(x);

步骤 3： 返回 element;

Pop 算法

以下是从队列中删除元素的步骤

步骤 1： 考虑两个队列，即 Q1 和 Q2，我们想从队列中删除一个元素。

步骤 2： 如果 !Q1.isEmpty() 则

             size:= Q1.size();

             对于 i=0…size-1 执行

             Q2.enqueue(Q1.dequeue());

             结束

             int item = Q1.dequeue();

             对于 j=0…size-1 执行

             Q1.enqueue(Q2.dequeue());

             结束