数据结构中的数组

数组是一种数据结构，它是同类型数据项的集合，存储在连续的内存位置。它是计算机编程中最简单的数据结构之一。在数组中，可以使用其索引号随机访问每个数据项。

基本术语

• 数组元素：数组中的项称为元素，它们存储在数组中，可以通过索引号随机访问。
• 数组索引：在数组中，元素通过其索引进行识别。数组索引从0开始。换句话说，数组采用零基索引。
• 数组长度：数组中的元素数量决定了数组的长度。
• 连续内存：数组元素在内存中紧密排列，以便快速访问。

数组的内存表示

数组中的所有元素都存储在连续的内存位置。因此，如果我们初始化一个数组，数组的元素将按顺序存储在内存中。这允许对元素进行有效的操作和访问。

内存计算

这是数组使用的总内存（物理大小）。数组占用的总内存可以通过以下公式计算：

注意：数组元素的大小取决于数据类型。例如，如果数组是int类型，那么每个元素是4个字节。

如果一个int类型的数组有5个元素，那么数组占用的总内存将是20个字节，因为char是4个字节。

类似地，如果一个char类型的数组有100个元素，那么数组占用的总内存将是200个字节，因为char是2个字节。

数组的大小或长度

这是数组包含的元素数量（逻辑大小）。例如，如果一个数组包含10个元素，那么数组的大小或长度将是10。

数组索引

1. 0（零基索引）：数组的第一个元素将是arr[0]。
2. 1（一基索引）：数组的第一个元素将是arr[1]。
3. n（n-基索引）：数组的第一个元素可以位于任何随机索引号。

数组声明

在不同的语言中，数组的声明方式可以不同。为了更好地理解，以下是其他语言中数组声明的一些示例。

在 Python 中实现

Java 实现

C++ 中的实现

C 语言实现

C#中的实现

数组初始化

数组的初始化方式在不同语言中可能不同。为了更好地理解，以下是其他语言中数组初始化的一些示例。

在 Python 中实现

Java 实现

C++ 中的实现

C 语言实现

C#中的实现

为什么我们需要数组？

假设我们需要跟踪一个科目（例如英语）在一个班级（例如10年级）的学生成绩。还假设10年级有30名学生。

那么，为了跟踪这些成绩，我们需要创建30个变量，每个学生一个。

我们看到，我们需要为30个变量编写代码，这不仅耗时且占用更多空间，而且管理30个变量也很困难。这意味着，如果我们想存储大量的实例，那么用30个普通变量来管理它们将是一项繁琐的任务。在这种情况下，数组会非常有用。

将此代码片段与前面的代码进行比较，我们可以看到我们只写了一行，而不是上一代码片段中的30行。它不仅减少了编写时间，而且易于管理。在这里，数组的每个元素都代表每个学生英语科目的成绩。

数组类型

数组可以根据其大小和维度进行分类。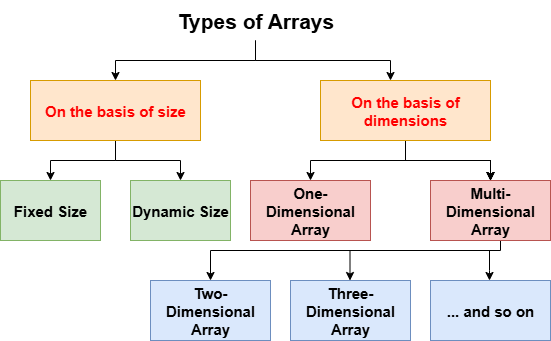

数组的类型：按大小分类

1. 固定大小数组

固定大小的数组是指其大小无法更改的数组。这些数组的缺点是，如果不知道数组大小并声明了一个较大的数组，但只使用了少量元素，就会造成内存浪费；或者如果数组声明的大小较小，则可能空间不足以存储所有元素。在这种情况下，不推荐使用静态内存分配。

在 Python 中实现

Java 实现

C++ 中的实现

C 语言实现

C#中的实现

2. 动态大小数组

在这些数组中，内存的分配和释放大部分是动态进行的。数组的大小会根据用户在代码执行期间的需求而变化，因此程序员不必担心数组大小。可以根据需要添加和删除元素。

在 Python 中实现

Java 实现

C++ 中的实现

C 语言实现

C#中的实现

数组的类型：按维度分类

1. 一维数组（1D Array）：可以将一维数组想象成单行，其中元素按顺序一个接一个地存储。它只有一个维度。
2. 多维数组：包含多个维度的数组称为二维数组。可以使用多维数组存储表格形式的数据。在多维数组中，我们可以有2D数组、3D数组等。

数组操作

在数组中，我们可以执行以下操作：

1. 数组遍历

顺序遍历数组以访问和处理元素称为数组遍历。数组遍历是计算机编程中最基本的操作之一。这是因为数组是常用的数据结构，用于在一个变量中存储多个元素。在数组遍历中，每个元素都从开始到结束进行访问，或者有时从结束到开始（即从后往前）。数组遍历通常使用循环来完成。

数组遍历的工作原理

创建数组时，会分配一块连续的内存，其中元素以索引方式存储。在数组中，可以使用索引访问每个元素，在大多数计算机编程语言中，索引从0开始。

例如，观察以下包含六个整数的数组：

这里，40位于索引0处，可以通过arr[0]访问。50位于索引1处，可以通过arr[1]访问。60位于索引2处，可以通过arr[2]访问。类似地，最后一个元素90位于索引5处，可以通过arr[5]访问。

数组遍历的类型

线性（顺序）遍历：它涉及从头到尾遍历数组的元素。这是最常见的数组遍历，用于搜索元素、打印元素和进行计算。

• Python
• Java
• C
• C++
• C#

输出

Linear (Sequential) Traversal: 
Elements of the array are: 40 50 60 70 80 90 

反向遍历：它涉及从头到尾遍历数组的元素。用于按反向顺序处理元素。

• Python
• Java
• C
• C++
• C#

输出

Reverse Array Traversal: 
Elements of the array are: 90 80 70 60 50 40   

2. 数组插入

在数组中添加新元素并保持数组中现有其他元素顺序的过程称为数组插入。由于数组存储在连续的内存位置，因此插入新元素需要移动数组中现有的元素。

数组插入的工作原理

数组的元素一个接一个地排列。因此，当在数组中插入新元素时，会发生以下情况：

1. 定位位置（索引）：必须知道新元素将要插入的位置。
2. 移动元素：找到索引后，必须将索引之后的所有元素移动到紧邻的下一个内存位置，以便为新元素腾出空间。
3. 插入新元素：现在，我们将新元素放在其适当的位置。

例如，观察以下包含六个整数的数组：

如果我们要在索引2处插入元素55，那么插入后更新的数组将是：

我们看到，元素60、70、80和90被向右移动，为新元素55腾出了空间。

插入的类型

在索引0处插入（在开头）：必须将每个现有数组元素向右移动一个位置。请注意，这种情况效率不高，因为它会影响数组中的所有现有元素。

• Python
• Java
• C
• C++
• C#

输出

Before insertion, the array is: 
11 21 31 41 51 61 
After insertion, the array is: 
52 11 21 31 41 51 61 

在特定索引处插入：在数组中特定索引处插入后，该索引之后的所有现有元素都会向右移动。

• Python
• Java
• C
• C++
• C#

输出

Before insertion, the array is: 
11 21 31 41 51 61 
After insertion, the array is: 
11 21 31 52 41 51 61 

在末尾插入：这是最简单的情况，因为不需要移动元素。

• Python
• Java
• C
• C++
• C#

输出

Before insertion, the array is: 
11 21 31 41 51 61 
After insertion, the array is: 
52 11 21 31 41 51 61  

3. 数组删除

在数组中，删除是从给定位置移除元素的过程，同时保持其余元素的顺序。移除数组中的一个元素需要移动元素来填补空隙。

1. 定位位置（索引）：必须知道要从哪个索引移除元素。
2. 移动元素：删除元素后，必须将删除发生索引之后的所有元素向左移动。
3. 更新大小（如果需要）：在动态内存分配的情况下，删除元素后大小会减小。

例如，观察以下包含六个整数的数组：

如果我们要在索引2处删除元素60，那么删除后，更新的数组将是：

我们看到，元素70、80和90被向左移动。

删除的类型

删除索引0处的元素（在开头）：必须将每个现有数组元素向左移动一个位置。

• Python
• Java
• C
• C++
• C#

输出

Before the deletion, the array is: 
11 21 31 41 51 61 
After the deletion, the array is: 
21 31 41 51 61 

在特定索引处删除：在数组中特定索引处删除后，该索引之后的所有现有元素都会向左移动。在以下程序中，我们将考虑零基索引来删除元素。

• Python
• Java
• C
• C++
• C#

输出

Before the deletion, the array is: 
11 21 31 41 51 61 
After the deletion, the array is: 
11 21 31 51 61 

在末尾删除：由于删除发生在末尾，因此不需要移动元素。

• Python
• Java
• C
• C++
• C#

输出

Before the deletion, the array is: 
11 21 31 41 51 61 
After the deletion, the array is: 
11 21 31 41 51 

4. 搜索

数组搜索是在给定元素数组中查找特定元素的过程。任务是找出元素是否存在于给定数组中。如果找到元素，则返回其位置。

搜索的类型

1. 线性搜索（顺序搜索）

线性搜索，也称为顺序搜索，是最简单的搜索算法。在线性搜索中，通常使用循环遍历数组。在每次迭代中，将一个元素与目标元素进行比较。

如果元素值与目标值匹配，则返回元素的索引；否则，在下一次迭代中将下一个元素与目标元素进行比较。在最坏的情况下，输入数组的每个元素只被遍历一次，从而使时间复杂度为O(n)。

• Python
• Java
• C
• C++
• C#

输出

The element is found at the position: 5 

2. 二分搜索

二分搜索仅适用于已排序的数组。在二分搜索中，首先找到给定数组的中间元素。然后，将其与目标元素进行比较。如果中间元素等于目标元素，则返回中间元素的索引。

如果目标元素大于中间元素，则将给定数组缩小到中间元素之后的所有元素，然后重复该过程。如果目标元素小于中间元素，则将给定数组缩小到中间元素之前的所有元素，然后重复该过程。

在时间复杂度方面，它比线性搜索更好，为O(log(n))。因为二分搜索只检查数组的一半，然后检查一半的一半，依此类推。因此，不是所有给定数组的元素都被遍历。

• Python
• Java
• C
• C++
• C#

输出

The element is found at the position: 5 

数组操作时间复杂度

数组数据结构的应用程序

以下是数组的一些应用程序。

• 高效存储：数组将相同类型的多个元素存储在连续的内存中，通过索引访问速度极快（检索时间为O(1)）。
• 基于索引的映射：与哈希表相比，在处理小整数范围时（例如，频率计数器或桶排序）是更快的替代方法。
• 访问数据：数组按特定顺序保存元素。因此，它允许在O(1)的恒定时间内访问任何元素。
• 搜索：如果数组元素已排序，我们可以在O(log n)的时间内搜索一个项。我们还可以有效地查找上限（ceiling）、下限（floor）、第k小的元素、第k大的元素等。
• 矩阵：可以使用二维数组来实现矩阵。
• 其他数据结构的实现：可以使用数组轻松实现栈和队列。甚至双端队列也可以通过数组实现。
• 在动态规划中的应用：动态规划算法中的中间结果通常存储在数组中。这些中间结果对于解决更大的问题非常有帮助。
• 数据缓冲区：数组还可以用作数据缓冲区，临时存储传入数据，如文件流、网络数据包和数据库结果，然后再进行处理。
• 多维建模：二维数组非常适合矩阵运算、图（邻接矩阵）和游戏（如数独或棋盘）。

数组数据结构的优点

• 快速高效访问：数组允许以恒定的访问时间快速高效地访问集合中的任何元素。这是因为数据存储在连续的内存位置。
• 内存效率：由于数组的元素存储在连续的内存中，因此减少了内存碎片。
• 多功能性：数组可用于存储整数、字符串、浮点数、字符，甚至指针和对象。
• 硬件兼容性：数组数据结构通常与大多数硬件架构兼容。因此，它在计算机编程领域是一个通用的工具。

数组数据结构的缺点

• 固定大小：通常，数组的大小是固定的。因此，扩展数组需要更多的内存。而且，由于需要复制数组的元素，这会更耗时。因此，数组扩展是内存密集且耗时的。
• 内存分配问题：大数组的分配可能导致内存耗尽。这可能导致崩溃，尤其是在资源有限的系统上。
• 插入和删除的挑战：由于元素紧密地存储在一起，并且添加或删除元素需要移动后续元素，这使得这些插入或删除操作效率低下。
• 数据类型支持有限：数组仅支持相同类型的文件，这限制了它们与复杂数据类型的用法。
• 灵活性问题：由于数组的大小固定且仅支持一种类型的文件，因此数组的适应性不如树或链表等结构。

结论

尽管存在许多缺点（如上所述），但数组在编程中仍然是不可或缺的，因为它们在处理相同数据类型的集合方面足够高效。理解数组对于构建可扩展的软件系统和高效的算法非常重要。

数组数据结构选择题

1) __________ 元素存储在连续的内存位置。

1. 链表
2. 树
3. 图
4. Array

2) 在动态规划中，哪个数据结构主要用于存储中间结果？

1. 链表
2. 数组
3. 图
4. 树

3) _________ 不支持动态数组。

1. C 语言
2. C# 语言
3. C++ 语言
4. Python 语言

4) 默认情况下，数组支持 _________ 索引。

1. 双索引
2. 单索引
3. 零索引
4. 三索引

5) 栈和队列可以使用 _____________ 实现。

1. Array
2. Graph
3. Tree
4. 以上全部