从 2D 矩阵构建链表

许多计算机科学算法和应用程序都使用链表和矩阵作为基本数据结构。链表将数据存储在通过指针连接的节点中，从而实现高效的元素插入和删除。矩阵将数据排列成表格状的二维行和列网格。将数据从一种结构转换到另一种结构通常很有用。

本文中，我们将研究一种从二维（2D）矩阵元素构造单向链表的算法。该算法将逐行迭代2D矩阵，为每个元素创建一个新节点并将其链接到前一个节点。这将构建一个链表，其中包含矩阵中所有按行顺序出现的元素。

我们将提供Python中的分步实现。代码将演示如何迭代2D列表结构，动态分配节点对象，并通过更新指针引用将它们链接在一起。

从矩阵构造链表可以实现这些标准数据结构之间的转换。这允许利用两种表示的优点来组织和访问数据。理解这些基本实现还可以培养处理指针、动态内存分配和一般链式数据结构的核心技能。

什么是2D矩阵？

2D矩阵，即二维数组，是一种以表格形式（行和列）存储元素的数据结构。它可以被视为一个值表或网格。

在数学上，矩阵有m行n列，共有m x n个元素。每个元素由其行索引i和列索引j标识。

例如，一个有3行4列的矩阵M将如下所示：

第一行是M[0]，第二行是M[1]，第三行是M[2]。

类似地，第一列是M[][0]，第二列是M[][1]，依此类推。

因此，每个元素可以按如下方式访问：

M[i][j]

其中i是行索引，j是列索引。

2D矩阵的关键属性

• 维度： 矩阵有两个维度——行和列。其大小由行数（m）和列数（n）定义。
• 元素类型： 矩阵可以包含任何数据类型的元素——整数、浮点数、字符等——但矩阵中的所有元素都是相同类型的。
• 矩形网格： 元素存储在具有固定行和列的矩形2D网格中。
• 连续存储： 元素在内存中按行连续存储。因此，行元素彼此相邻存储。
• 索引： 使用带行和列索引的[ ]符号访问单个元素。索引从0开始。
• 数学运算： 矩阵支持加法、减法、乘法、转置等数学运算。这些操作是元素级的。
• 方阵： 如果行数（m）=列数（n），则为方阵。方阵具有特殊属性。
• 对称矩阵： 等于其转置的方阵，即A = AT。对角线上的元素相等。
• 单位矩阵： 对角线上为1，其余为0的方阵。相乘时，它使原始矩阵保持不变。
• 稀疏矩阵： 大部分元素为零的矩阵称为稀疏矩阵。可以使用特殊的存储技术。
• 稠密矩阵： 大部分元素为非零的矩阵称为稠密矩阵。显式存储所有元素。

矩阵具有明确定义的数学属性和运算，使其成为线性代数、图论、物理学、工程学和许多其他领域问题不可或缺的分析工具。矩形网格结构允许组织存储数据以进行计算。

2D矩阵在计算机科学中有广泛的应用

• 存储表格数据（数据库）
• 表示图像（2D网格中的像素）
• 游戏地图和网格
• 神经网络权重矩阵
• 图邻接矩阵

许多算法涉及对2D矩阵数据结构进行操作，例如矩阵乘法、转置、旋转、搜索、排序、寻路等。

总而言之，2D矩阵是一种基本的数据结构，用于以二维表格状结构存储和组织数据，并通过行和列索引高效访问元素。

实现矩阵的不同方式

• 一维数组： 最简单的实现是使用大小为 * mn 的一维数组来按行存储所有元素。元素 (i,j) 映射到数组索引 i * n + j。
• 二维数组： 使用二维数组或嵌套数组来存储行和列更为直观。每行可以存储为单独的一维数组。
• 动态数组： 矩阵可以使用动态数组创建，例如 C++ 中的向量或 Java 中的 ArrayLists，它们可以根据需要调整大小。
• 指针的指针： 一个指针数组，每个指针指向一个行数组。允许行具有不同的长度。
• 行主序与列主序： 像 C 这样的语言按行存储数组，因此行是连续存储的。在列主序中，列是连续存储的。
• 类/结构体： 矩阵可以实现为包含行和列数据成员以及指向数据数组的指针的类或结构体。
• 矩阵库： 许多语言提供具有优化实现和操作的矩阵库，例如 Python 的 NumPy 和 Matlab 中的 Matrix 类。
• 压缩存储： 稀疏矩阵可以使用压缩存储，例如压缩行存储，只存储非零值，从而减少内存使用。
• 并行化： 矩阵操作（如乘法）可以并行化，以利用多个 CPU 和 GPU 实现高性能。

总而言之，矩阵可以通过多种方式在代码中实现，在空间和时间复杂度方面提供不同的权衡。最佳实现取决于语言、数据大小、算法和性能要求。矩阵能够编写优化的数学代码。

算法和Python实现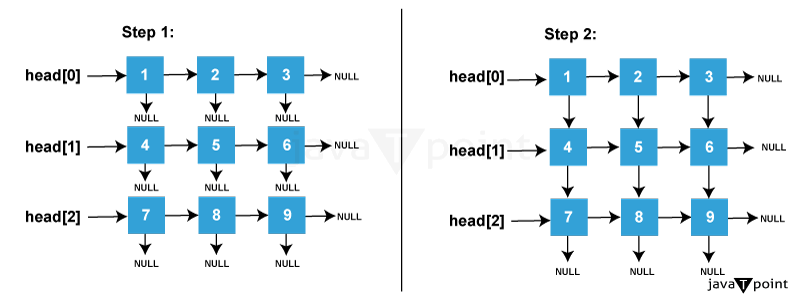

算法

1. 创建一个Node类来表示链表中的每个节点。它将包含一个数据字段和一个指向下一个节点的next字段。
2. 声明一个头节点并将其初始化为null，以标记链表的开始。
3. 使用两个嵌套的for循环逐行遍历2D矩阵。
4. 对于每个元素，动态分配一个新的Node并使用元素值初始化其数据字段。
5. 要链接每个Node，请检查头是否为null。如果是，则将头设置为此新Node。否则，将前一个Node的next设置为此新Node。
6. 请跟踪尾节点并为每个创建的新Node推进它。
7. 链接所有元素后返回最终的头节点。

实施

• 使用嵌套循环按行和列索引迭代2D数组。
• 在循环内部使用malloc()或new运算符动态分配一个新的Node对象。
• 将Node的数据字段设置为当前元素的值。
• 如果头为null，则将头分配给此新Node。
• 否则，请找到当前尾节点，并将其next设置为新节点的尾部。
• 推进尾指针。
• 完全迭代后返回头。

分析

• 时间复杂度： 遍历整个矩阵为O(mn)。
• 空间复杂度： 为每个元素分配节点为O(mn)。
• 使用动态分配和指针来构建链式结构。
• 逐行遍历保持与矩阵相同的顺序。

此实现演示了动态分配、指针操作、链表构建和迭代多维数组等核心概念。

Python 代码

输出

• 我们定义了一个Node类来表示每个链表节点
• constructLinkedList函数迭代矩阵并为每个元素创建一个新节点
• 它设置next指针以将节点链接在一起
• 最后，它返回头节点
• 我们通过遍历temp指针来打印最终的链表

输出显示链表包含按行顺序排列的矩阵元素。

这演示了将2D矩阵动态转换为线性链表结构。同样的方法也可以扩展到其他数据结构。