排序大整数

排序是一个过程，在计算机科学领域，它涉及按顺序排列数据，以提高处理和分析的效率。然而，当处理超出标准数据类型限制的数字时，排序变得相当具有挑战性。这些超大数字被称为“大整数”，用于密码学、科学计算、金融计算以及其他需要精确处理海量数据的领域。

传统排序方法是为固定大小的数字设计的，在面对大整数的复杂性时会遇到困难。为了解决这个问题，已经开发出专门的技术，例如**基数排序、桶排序和归并排序的修改版本**。这些方法利用策略、优化和数据结构来组织和处理海量数值。

什么是大整数？

• 像整数和长整数这样的传统数据类型有有限的范围，限制了它们可以表示的数字大小。
• 许多实际应用，例如密码学、科学计算、金融计算和数学研究，都需要使用超出这些传统限制的大整数。
• **示例**包括用于加密的大素数、天文计算、精确的财务计算以及数论和组合学中的问题。
• 为了处理这些极其大的整数，使用了专门的数据结构或库，提供了对任意精度算术的支持。
• 大数通常显示为数组、字符串或可以根据需要扩展以处理内存限制内的任何大小数字的专用数据类型。
• 当处理位数众多的数字时，像加法、减法、乘法和除法这样的数学运算会变得更加复杂。排序和比较大整数需要能够处理其独特表示和幅度的专用算法。
• 传统的基于比较的排序算法，如快速排序或归并排序，依赖于单个元素之间的比较，这使得大整数更加复杂。
• 由于这些独特的挑战，排序大整数是一项非琐碎的任务，需要专门的算法和技术。
• 这些算法通常利用基数排序、桶排序的原理，或对传统排序算法的改编，以应对大整数带来的独特挑战。

不同的排序方法

• 一种解决这个问题的方法是利用 Python 中现有的 `sorted()` 函数。该函数能够排列代表整数的字符串列表。由于大整数可以表示为字符串，因此如果需要，一种解决方案是将它们转换为字符串，对列表进行排序，然后将它们转换回整数。
• 另一种方法是采用基数排序算法，该算法在排序整数方面效率很高。基数排序通过逐位对整数进行组织来工作，从最低有效位开始。它根据数字将整数分到存储桶中。然后合并这些存储桶以产生结果。
• 另一种方法可能是修改归并排序算法以适应大整数。归并排序作为一种分治算法，它递归地将输入数组分成两半，分别对它们进行排序，然后以特定方式将它们合并在一起。在处理大整数时，使用归并排序需要定义一个自定义比较函数，以从最高有效位开始比较这些大数字的各位。
• 最后，另一个选项是实现桶排序，它属于基于分配的排序算法。它通过将一组数字分成一定数量的桶，并根据它们的数值将数字放入各自的桶中来工作。然后，使用插入排序或快速排序等排序方法分别对每个桶进行排序。
• 在某些情况下，混合方法可能更有效。例如，我们可以使用基数排序对大整数进行初始分配到桶中，然后使用归并排序或其他高效算法对各个桶进行排序。
• 无论我们选择哪种算法，我们都必须考虑如何处理数字（例如使用字符串、数组或自定义数据类型）、如何有效地管理内存（尤其是在处理数据集时）以及如何寻找提高性能的方法（例如使用并行处理和对缓存内存友好的算法）。

方法 1：使用 sort 函数

输出

说明

• 我们首先创建一个名为 `big_numbers` 的列表，其中包含五个大整数。
• 为了显示 `big_numbers` 列表，我们使用 `print` 函数并加上消息“未排序的大整数”；`print("未排序的大整数\n", big_numbers)`。
  • 包含“\n”是为了在“未排序的大整数”文本后插入一行。
• 接下来，我们打印短语“已排序的大整数”。
• 然后，我们应用内置的 `sort()` 函数来组织 `big_numbers` 列表中的元素；`big_numbers.sort()`。
  • 此操作会重新排列列表，直接改变其顺序。
  • 默认情况下，`sort()` 按升序排列项目。
• 最后，我们通过 `print(big_numbers)` 打印出 `big_numbers` 的排序后版本。

方法 2：使用内置的 Sorted 函数

输出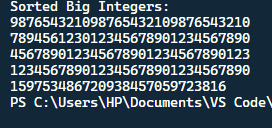

说明

• 代码以导入 `sys` 模块开始。
• 然后定义一个名为 `sort_big_integers()` 的函数，该函数接受一个整数列表作为输入。
• 在函数内：
  • 使用列表推导式将所有输入整数转换为字符串。
  • 使用内置的 `sorted()` 函数对字符串列表进行排序。
  • 为了按整数排序，每个字符串都使用 `=int` 被视为整数。
  • 通过设置 `reverse=True`，排序按降序进行。
  • 排序后的列表保存在 `sorted_ints` 中。
  • 该函数返回 `sorted_ints` 列表。
• 在函数外部，创建了一个名为 `big_numbers` 的列表，其中包含一些表示为字符串的大整数示例。
• 使用 `big_numbers` 作为参数调用 `sort_big_integers()` 函数。
• 从函数返回的排序列表存储在 `sorted_big_ints` 中。
• 最后，一个循环在一行中打印 `sorted_big_ints` 列表的每个元素。

方法 3：基数排序

输出

说明

• 代码中定义了 `radix_sort()` 函数来处理一个整数列表（`nums`）。
• 在函数内：
  • 它确定列表中所有整数中的最大位数。
  • 创建了十个列表，代表每个数字值（0-9）的存储桶。
• 排序是通过嵌套循环完成的；
  • 外层循环遍历每个数字位，从最低有效位开始。
  • 对于每个数字位，
    • 内层循环遍历输入列表中的每个数字。
    • 提取该数字在当前数字位上的数字。
    • 具有该数字值的数字被添加到相应的存储桶中。
  • 所有存储桶填满后，输入列表会被清空。
  • 来自所有存储桶的数字按照存储桶顺序重新组合到输入列表中。
  • 在处理完所有数字位后，会清除所有存储桶。
• 一旦处理完所有数字位，输入列表 `nums` 就被排序了。
• 最后，该函数返回排序后的列表。
• 在程序运行之前；
  • 我们定义了一个名为 `big_numbers` 的列表，其中包含示例。
  • 我们显示列表。
  • 然后我们调用 `radix_sort()` 函数，并将 `big_numbers` 作为输入。
  • 最后，我们打印出函数返回的列表。