矩阵沿对角线镜像

2025年3月17日 | 阅读 8 分钟

引言

将矩阵沿对角线镜像（通常称为对角线镜像或沿对角线反射）是线性代数和数学中的一项基本运算。此操作涉及以这样一种方式变换矩阵，使其相对于主对角线对称，从而创建原始矩阵的镜像。对角线镜像在矩阵分解、特征值计算和优化问题等领域具有广泛的应用。它在简化矩阵属性和运算方面发挥着关键作用。此操作对于理论理解以及数据分析、信号处理和各种科学学科中的实际应用都非常重要。在此背景下，我们将探讨将矩阵沿对角线镜像的原理和方法，并深入探讨其在数学中的重要性及其在解决实际问题中的实际效用。理解对角线镜像对于更深入地理解矩阵运算及其在不同学科中的应用至关重要。

给定一个 N x N 阶的二维数组，打印一个矩阵，该矩阵是给定树沿对角线的镜像。我们需要以一种交换对角线上方三角形的值与对角线下方三角形的值的方式打印结果，就像一个镜像交换。以矩阵布局打印所得的二维数组。

矩阵沿对角线镜像的属性

将矩阵沿对角线反射，也称为对角线镜像或沿对角线反射，在线性代数和各种数学运算中具有多种特性和影响。下面是一些与此操作相关的关键特性。

将矩阵沿对角线镜像的结果是一个对称矩阵。这意味着矩阵与其转置相等，对角线两侧的元素互为镜像。
特征值对角线镜像不会改变原始矩阵的特征值。然而，如果原始矩阵具有特征值 λ_1...λ_n，则镜像矩阵也将具有相同的特征值。
正交性是对角线镜像的过程。它是正交的，保持向量的点积。然而，如果存在向量 x 和 y，则点积 (xT)*(y) 与镜像矩阵的点积 (yT)*(x) 相同。
实对称矩阵对角线镜像特别适用于实对称矩阵，其中特征值为实数，特征向量是正交的。此操作保留了实对称属性。
特征值分解对于实对称矩阵，对角线镜像可以看作是一种正交变换，通过将其转换为对角线矩阵来对矩阵进行对角化。此过程是解决各种精细问题（包括特征值分解）的基础。
简化对角线镜像简化了矩阵计算，并允许更轻松地计算矩阵幂和指数，因为镜像矩阵保留了相同的特征值和正交特征向量。
应用对角线镜像广泛应用于量子力学、量子计算、药物和统计学等领域，其中实对称矩阵的特性至关重要。
不变性对角线镜像是一种等距操作，这意味着它保留了向量之间的距离和角度。此属性在需要保持几何变换的应用中非常宝贵。

实施

此问题的简单解决方案涉及冗余空间。我们一个接一个地切割每个右对角线（从右到左）。在遍历对角线期间，我们首先将所有元素压入堆栈，然后再次切割并用堆栈元素替换对角线的每个元素。

实现矩阵沿对角线镜像的基本程序如下

# Simple or basic program for implementing the mirror of a matrix using Python.
m = 100
def MM (matrix, size):
# For the diagonal of a matrix, which starts at the first row of the matrix.
r = 0
# Traversing of the right diagonal of the matrix.
for j in range(size):
# Stack is used here for reversing the elements of the matrix.
s = []
i = r
k = j
while (i < size and k >= 0):
s.append(matrix[i][k])
i += 1
k -= 1
# Pushing all the elements of the matrix into a stack in reverse order.
i = r
k = j
while (i < size and k >= 0):
matrix[i][k] = s[-1]
k -= 1
i += 1
s.pop()
# Doing the same process for the diagonals that start at the end of each column.
c = size - 1
for j in range (1, size): 
# The stack is used for reversing the elements here;
s = []
i = j
k = c
while (i < size and k >= 0):
s.append(matrix[i][k])
i += 1
k -= 1
# Pushing all the elements of the matrix into a stack in reverse order.
i = j
k = c
while (i < size and k >= 0):
matrix[i][k] = s[-1]
i += 1
k -= 1
s.pop()
# Function defined for the printing of the matrices.
def PM (matrix, size):
for i in range(size):
for j in range(size):
print(matrix[i][j], end=" ")
print()
# The driver code or the main code.
matrix = [[1, 2, 3, 4], [5, 6, 7, 8],
[9, 10, 11, 12], [13, 14, 15, 16]]
size = 4
print ("The matrix given is")
PM (matrix, size)
print ("The mirror matrix of the given matrix across the diagonal is:")
MM (matrix, size)
PM (matrix, size)

输出

上面编写的程序的输出如下所示

时间复杂度 O(n^2)

辅助空间 O(n)，因为使用了堆栈。

代码解释

手写的 Python 代码将一个方阵沿其主对角线镜像。下面是代码的详细解释。

代码首先定义了一个名为 MM（镜像矩阵）的函数和另一个名为 PM（打印矩阵）的函数，分别用于矩阵操作和打印。驱动程序代码初始化一个示例 4x4 矩阵并打印它。

MM 沿其主对角线作为输入矩阵。它分两部分完成此操作。

左上到右下倾斜：它遍历从左上角（行 0，列 0）到右下角（行大小 1，列大小 1）开始的倾斜。对于每个倾斜，它使用堆栈沿该倾斜反转元素的顺序。它将倾斜的元素压入堆栈，然后以相反的顺序将它们弹回矩阵。此操作针对所有此类倾斜完成。
**右上到左下倾斜** 此外，它处理从右上角（行 0，列大小 1）到左下角（行大小 1，列 0）开始的倾斜。它对这些倾斜使用相同的堆栈反转方法。

调用 MM 函数后，代码使用 PM 函数打印镜像矩阵。结果是一个行已反转的矩阵，有效地创建了原始矩阵沿其主对角线的镜像。

在给定的插图中，代码镜像了原始 4x4 矩阵，并打印了最终的镜像矩阵，显示了沿主对角线的变换。

方法 -2

通过输出观察矩阵揭示了此问题的成功修复：我们只需要切换 (mat[i][j] 到 mat[j][i])。

上面程序中的问题已使用下面给出的技术解决。

在 Python 中应用镜像矩阵的有效方法是使用列表推导通过交换原始矩阵的行和列来生成新矩阵。下面是您可以如何简洁有效地完成此操作。

python
def mirror_matrix( matrix):
    mirrored_matrix = ((matrix (j)( i) for j in range( len (matrix))) for i in range( len (matrix)))
    returnmirrored_matrix

此代码遍历原始矩阵的行和列，交换它们以生成镜像矩阵。它的运行时间为 O(n^2)，其中“n”是矩阵的大小，这使其成为创建输入矩阵沿其主对角线镜像的有效而简洁的结果。

# For finding the mirror of the matrix across the diagonal, the effective way is defined as follows.
from builtins import range
M = 100; 
def MM (matrix, size): 
# Traversing the matrix and swapping the elements. 
for i in range(size): 
for j in range (i + 1):
t = matrix[i][j]; 
matrix[i][j] = matrix[j][i] 
matrix[j][i] = t 
# The function used for printing the matrix. 
def PM (matrix, size): 
for i in range(size): 
for j in range(size): 
print(matrix[i][j], end=" "); 
print(); 
# The driver code or the primary code is as follows. 
if __name__ == '__main__': 
matrix = [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]; 
size = 4; 
print("The matrix that is to be processed or that is to be changed for mirror matrix:") 
print(matrix)
print("The matrix that is changed or the mirror matrix after the implementation of the program is:")
MM (matrix, size); 
PM (matrix, size); 

输出

上面编写的程序的输出如下所示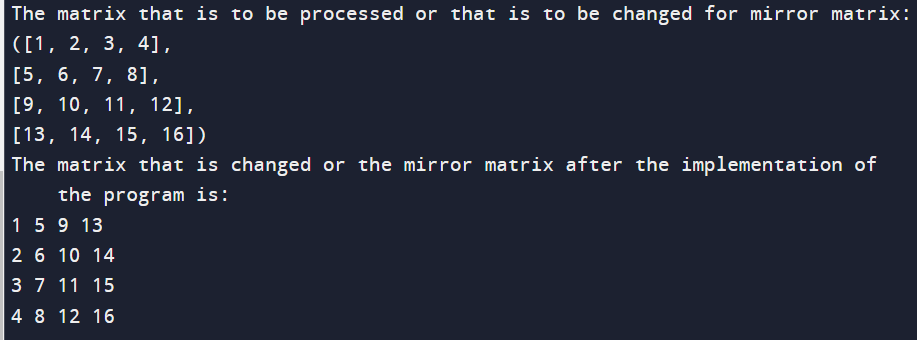

代码解释

此 Python 代码定义了一个程序来查找给定方阵的镜像矩阵。MM 函数将矩阵及其大小作为参数，它遍历矩阵的上三角形，交换主对角线上的元素。这种交换有效地转置了矩阵，从而形成了其镜像。PM 函数负责以可读格式打印矩阵元素。

在主部分（如果 name == ', main,'），初始化一个名为 matrix 的 4x4 矩阵，并打印其原始形式。然后通过调用 MM 函数获得镜像矩阵，并使用 PM 函数打印原始矩阵和镜像矩阵。

矩阵表示为列表的列表，其中每个内部列表对应于矩阵的一行。range 函数的使用有助于矩阵指示符的复制。

总的来说，该代码演示了一个简单的矩阵操作，提供了通过转置实现镜像矩阵过程的清晰说明。它作为理解嵌套循环、矩阵操作和 Python 编程基础知识的教育插图。

上述代码的复杂性。

由于用于矩阵转置和打印的嵌套循环，该代码的时间复杂度为 O(n^2)。空间复杂度为 O(n^2)，远低于将输入矩阵存储为列表的列表。临时变量具有常数空间。总的来说，该代码有效地找到了镜像矩阵，演示了二次时间复杂度和空间复杂度，其中 n 是方阵的大小。

结论

总之，Python 代码通过交换主对角线上的元素来有效地计算方阵的镜像矩阵。转置操作的时间复杂度为 O(n^2)，其中 n 是矩阵大小，因为存在嵌套循环。空间复杂度也为 O(n^2)，因为矩阵表示为列表的列表。该代码提供了简洁且具有指导意义的矩阵操作插图，说明了实现镜像的过程。它对于学习者特别有益，因为它演示了 Python 中类似于嵌套循环、矩阵遍历和转置的基本概念。总的来说，此代码对于那些寻求理解和应用主对角线上的矩阵变换的人来说是一个宝贵的资源。

下一个主题在给定数组中具有最长公共前缀的最大长度的字符串对

← prev next →

矩阵沿对角线镜像

引言

矩阵沿对角线镜像的属性

实施

方法 -2

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

矩阵沿对角线镜像

引言

矩阵沿对角线镜像的属性

实施

方法 -2

结论

相关帖子

值大于 k 的最长子数组

双向链表上的归并排序

打印所有匹配 CamelCase 约定字典的单词

树遍历

栈排列 (检查一个数组是否是另一个数组的栈排列)

O(N^2) 复杂度意味着什么

检查给定单词字符串是否能由字典中的单词组成

查找最近的回文数

第 k 大的连续子数组和

稀疏矩阵的类型

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器