Prim 算法和 Kruskal 算法的区别

引言

在图论领域，寻找给定图的最小生成树（MST）是一个常见的具有众多应用的问题。最小生成树在网络设计、聚类和优化等各个领域都有应用。解决这个问题的两种流行算法是 Prim 算法和 Kruskal 算法。虽然两种算法都旨在找到图的最小生成树，但它们的方法和所依赖的基本原理有所不同。

Prim 算法

Prim 算法是一种贪心算法，它从一个起始顶点开始逐渐增长最小生成树。该算法维护两个顶点集：一个集合包含已包含在 MST 中的顶点，而另一个集合包含剩余顶点。Prim 算法通过迭代选择连接这两个集合且具有最小边权重的顶点，并将其添加到 MST 中。

该算法遵循以下步骤：

• 初始化：选择一个起始顶点并将其标记为已访问。
• 找到连接到已访问顶点的最小权重边。

为完成此操作，请检查所有连接到已访问顶点的边，并选择权重最低的边。

• 选择权重最低的边并将其添加到 MST 中。
• 将新添加的顶点标记为已访问。
• 重复步骤 2-4，直到所有顶点都被访问。

Prim 算法的关键特征

Prim 算法是一种贪心方法，因为它在每一步都做出局部最优选择来构建 MST。

它保证生成一个连通的无环 MST。

使用邻接矩阵的简单实现，Prim 算法的时间复杂度为 O(V^2)。但是，使用优先队列可以将复杂度降低到 O(E log V)。

程序

说明

• 主函数首先要求用户输入图中顶点的数量和边的数量。
• 它创建了一个名为 graph 的二维向量来表示图的邻接列表。向量的大小由顶点的数量决定。
• 然后，程序逐一要求用户输入图的边。对于每条边，都会提示用户输入源顶点、目标顶点和边的权重。然后将该边添加到源顶点和目标顶点的邻接列表中。
• 用户被要求输入将从中构建最小生成树的起始顶点。
• 调用带有 graph 和 startVertex 参数的 primMST 函数。
• 在 primMST 函数内部，从 graph 向量的大小确定顶点的数量。
• 初始化三个向量 key、parent 和 included。key 向量存储每个顶点的最小权重，parent 向量存储 MST 中每个顶点的父节点，included 向量跟踪一个顶点是否已包含在 MST 中。
• 创建了一个名为 pq 的优先队列，用于存储顶点及其键值对。优先队列使用 greater 比较器实现为最小堆，确保具有最小键值的顶点位于顶部。
• 将起始顶点添加到优先队列，键值为 0。
• 程序进入一个循环，直到优先队列 pq 为空。
• 在循环的每次迭代中，从优先队列中提取具有最小键值的顶点。此顶点被标记为包含在 MST 中。
• 然后，程序遍历提取顶点的所有相邻顶点。对于每个尚未包含在 MST 中且边权重小于其当前键值的相邻顶点，将更新键值，将父节点设置为提取的顶点，并将该顶点添加到优先队列中。
• 循环结束后，通过遍历 parent 数组来打印最小生成树。parent 数组中的每个条目都代表 MST 中的一条边，程序会打印除起始顶点以外的每个顶点的父子关系。

程序输出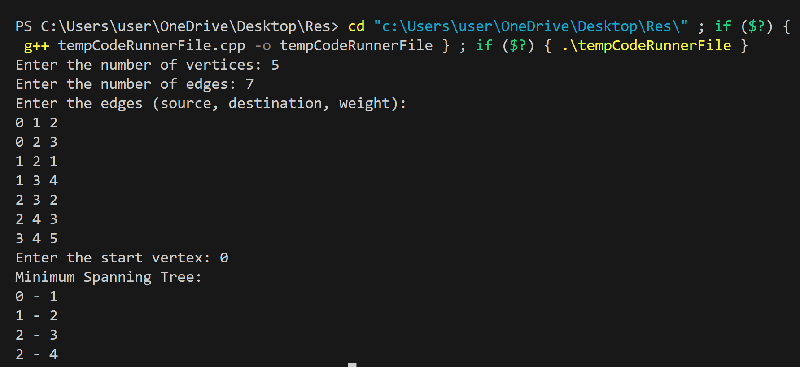

Kruskal 算法

Kruskal 算法是另一种用于查找最小生成树的贪心算法。与 Prim 算法不同，Kruskal 算法按边的权重升序处理图的边。它在不创建环路的情况下，逐步将边添加到 MST 中。

Kruskal 算法涉及的步骤如下：

• 按权重非递减顺序对所有边进行排序。
• 将一个空图初始化为 MST。
• 按排序顺序考虑边，如果它们不形成环路，则将它们添加到 MST 中。

为确定添加一条边是否会形成环路，Kruskal 算法利用了不相交集合的概念。它跟踪包含每个顶点的子集，并检查添加一条边是否连接了同一子集中的两个顶点。

Kruskal 算法的关键特征

Kruskal 算法使用不相交集合的概念来有效检测环路。

它不需要起始顶点，也不限于连通图。

Kruskal 算法的时间复杂度为 O(E log E) 或 O(E log V)（使用高效的排序算法），其中 E 表示边的数量，V 表示顶点的数量。

程序

说明

• DisjointSet 结构有两个向量：parent 和 rank。parent 向量存储每个顶点的父节点，rank 向量用于优化不相交集数据结构中的 union 操作。
• 然后，程序定义了几个辅助函数。createSet 函数通过将每个顶点分配给自己独立的集合来初始化不相交集。find 函数使用路径压缩查找元素所属的集合。
• unionSets 函数按秩执行两个集合的并集，确保较小的集合始终合并到较大的集合中。compareEdges 函数是一个比较器，用于按权重非递减顺序对边进行排序。
• kruskalMST 函数以边向量和顶点数量作为输入，并返回代表最小生成树的边向量。
• 它初始化一个空的 result 向量，并使用 createSet 创建一个不相交集。然后使用 sort 函数和 compareEdges 比较器按权重非递减顺序对边进行排序。
• 然后，程序遍历排序顺序中的每一条边。对于每条边，它使用 find 函数查找源顶点和目标顶点所属的集合。
• 如果集合不同，则表示顶点尚未连接，则将该边添加到 result 向量，并使用 unionSets 合并集合。
• 最后，调用 printMST 函数显示最小生成树。它打印 MST 中的每条边及其权重，并计算 MST 的总权重。
• 在主函数中，用户被提示输入图中顶点的数量和边的数量。然后，从用户那里获取每条边的详细信息（源、目标和权重）。
• 调用 kruskalMST 函数，并传入输入图和顶点，然后使用 printMST 打印生成的最小生成树。

程序输出

方法的差异

方法

Prim 算法采用基于顶点的方法，专注于从起始顶点生长 MST。它通过添加连接到已访问顶点的最小权重边来逐渐扩展树。

Kruskal 算法采用基于边的方法，对边进行排序，并在它们不形成环路的情况下将它们添加到 MST 中。它通过按权重升序逐个考虑边来构建 MST。

连接性

Prim 算法即使对于不连通的输入图，也能确保 MST 始终连通。它从一个顶点开始，然后逐渐扩展树，直到包含所有顶点。

在不连通图的情况下，Kruskal 算法可以生成多个树。它最初将每个顶点视为单独的树，并在添加边时将它们合并，从而形成一个树的森林。

时间复杂度

Prim 算法使用简单的实现，时间复杂度为 O(V^2)，使用优先队列的时间复杂度为 O(E log V)。实现的具体选择取决于图的密度。

Kruskal 算法的时间复杂度为 O(E log E) 或 O(E log V)（使用高效的排序算法）。它主要取决于边的数量而不是顶点的数量。

Prim 算法的优点

效率： Prim 算法在边数接近最大可能值的稠密图上表现良好。其使用邻接矩阵表示法的时间复杂度为 O(V^2)。

保证 MST： Prim 算法保证在 V-1 次迭代内找到 MST，其中 V 是图中的顶点数。

简单性： Prim 算法相对容易理解和实现，是教育目的的热门选择。

Prim 算法的缺点

需要连通图： Prim 算法假定图是连通的。如果图有不连通的分量，则需要将该算法分别应用于每个分量以找到它们各自的最小生成树。

无法处理负权重： Prim 算法无法处理带有负边权重的图，因为这可能导致不正确的 MST 结果。

稀疏图上的性能： 对于边数明显较少的稀疏图，Prim 算法的效率可能低于 Kruskal 算法。

Prim 算法的应用

网络设计： Prim 算法通常用于网络设计场景，以找到连接各个位置的最低成本网络，从而最大限度地降低总体连接成本。

聚类分析： 它可以应用于识别网络中的簇或社区，其中每个簇由最小生成树的子树表示。

Kruskal 算法的优点

处理不连通图： Kruskal 算法自然地处理不连通图，并生成最小生成森林，该森林由每个连通分量的多个 MST 组成。

处理负权重（无负环）： Kruskal 算法可以处理带有负边权重的图，只要图中没有负环。

稀疏图效率： Kruskal 算法在边数明显较少的稀疏图上表现更好。其时间复杂度为 O(E log E)，其中 E 是边的数量。

Kruskal 算法的缺点

排序开销： Kruskal 算法需要根据权重对边进行排序，这会引入额外的 O(E log E) 时间复杂度。

潜在的森林输出： 在不连通图的情况下，Kruskal 算法可能会生成多个最小生成树的森林，这对于某些应用可能不理想。

Kruskal 算法的应用

网络连通性： Kruskal 算法通过找到最小生成森林（代表组件之间的连接）来确定网络是否完全连通，从而非常有用。

图像分割： 它可以应用于图像处理任务，通过将像素视为顶点，将像素之间的相似性视为边权重，将图像划分为不同的区域。