二项堆

2025年4月28日 | 阅读 11 分钟

在本文中，我们将讨论二项堆。在开始讨论主题之前，我们应该先了解一些基本术语，如堆、最小堆、最大堆和二项树。

什么是堆？

堆是一个完全二叉树，二叉树是指节点最多有两个子节点的树。堆有两种类型，定义如下：

最小堆：父节点的值应小于或等于其任何一个子节点。
数学上，最小堆可以定义为：
A[父节点(i)] <= A[i]
最大堆：父节点的值大于或等于其子节点。
数学上，最大堆可以定义为：
A[父节点(i)] >= A[i]

什么是二项树？

二项树 B_k 是一棵递归定义的有序树，其中 k 定义为二项树的阶。

如果二项树表示为 B₀，则该树由单个节点组成。
一般而言，B_k 由两棵二项树组成，即 B_k-1 和 B_k-1，它们被链接在一起，其中一棵树成为另一棵二项树的左子树。

我们可以通过下面的例子来理解这一点。

如果 B₀，其中 k 为 0，则树中只有一个节点。

如果 B₁，其中 k 为 1。因此，将存在两棵 B₀ 的二项树，其中一棵 B₀ 成为另一棵 B₀ 的左子树。

如果 B₂，其中 k 为 2。因此，将存在两棵 B₁ 的二项树，其中一棵 B₁ 成为另一棵 B₁ 的左子树。

如果 B₃，其中 k 为 3。因此，将存在两棵 B₂ 的二项树，其中一棵 B₂ 成为另一棵 B₂ 的左子树。

现在，让我们开始主要主题“二项堆”。

什么是二项堆？

二项堆可以定义为满足堆属性（即最小堆）的二项树的集合。最小堆是一种堆，其中每个节点的值都小于其子节点的值。二项堆主要用于实现优先队列。它是二叉堆的扩展，除了二叉堆提供的其他操作外，还提供了更快的合并或联合操作。

二项堆的属性

对于具有 n 个节点的二项堆，有以下属性：

堆中的每棵二项树都必须遵循 **最小堆** 属性，即节点的键值大于或等于其父节点的键值。
对于任何非负整数 k，堆中至少应存在一棵根节点度为 k 的二项树。

堆的第一个属性确保了整个堆都满足最小堆属性。而上面列出的第二个属性确保了具有 n 个节点的二叉树最多应有 1 + log₂ n 棵二项树，其中 **log₂** 是以 2 为底的对数。

我们可以借助一个例子来理解上面列出的属性：

上图中有三棵二项树，即 B₀、B₂ 和 B₃。上面这三棵二项树都满足最小堆的属性，因为所有节点的值都小于子节点的值。

上图也满足二项堆的第二个属性。例如，如果我们考虑 k 的值为 3，我们可以从图中观察到度为 3 的二项树存在于堆中。

二项堆与数字的二进制表示

具有 n 个节点的二项堆包含的二项树数量等于 n 的二进制表示中设置为 1 的位数。

假设我们要创建一个具有 'n' 个节点的二项堆，这可以通过 'n' 的二进制数简单定义。例如：如果我们想创建一个具有 13 个节点的二项堆；13 的二进制形式是 1101，如果我们从最右边的数字开始编号，那么我们可以观察到在第 0、2 和 3 位存在 1；因此，具有 13 个节点的二项堆将包含 B₀、B₂ 和 B₃ 二项树。

我们可以用另一个例子来更清楚地理解这一点，假设我们要创建一个具有 9 个节点的二项堆。9 的二进制表示是 1001。因此，在 9 的二进制表示中，数字 1 出现在第 0 位和第 3 位，因此，二项堆将包含度为 0 和 3 的二项树。

现在，让我们继续讨论在二项堆上执行的操作。

二项堆上的操作

可以在二项堆上执行的操作列出如下：

创建二项堆
查找最小键
两个二项堆的联合或合并
插入节点
提取最小键
减少键值
删除节点

现在，让我们详细讨论上述操作。

创建新的二项堆

当我们创建一个新的二项堆时，它只需要 O(1) 时间，因为创建堆会创建一个堆头，其中不附加任何元素。

查找最小键

如上所述，二项堆是二项树的集合，并且每棵二项树都满足最小堆属性。这意味着根节点包含最小值。因此，我们只需要比较所有二项树的根节点即可找到最小键。在二项堆中查找最小键的时间复杂度为 **O(logn)**。

两个二项堆的联合或合并

这是在二项堆上执行的最重要的操作。堆的合并可以通过比较两棵树根节点的键值来完成，键值较大的根节点将成为键值较小的根节点的子节点。查找联合的时间复杂度为 O(logn)。合并两棵树的函数如下：

function merge(a,b)
if a.root.key ? b.root.key
return a.add(b)
else
return b.add(a)

要执行两个二项堆的联合，我们必须考虑以下情况：

情况 1：如果 degree[x] 不等于 degree[next x]，则将指针向前移动。

情况 2：如果 degree[x] = degree[next x] = degree[sibling(next x)]，则

将指针向前移动。

情况 3：如果 degree[x] = degree[next x] 但不等于 degree[sibling[next x]]

并且 key[x] < key[next x]，则从根节点删除 [next x] 并将其附加到 x。

情况 4：如果 degree[x] = degree[next x] 但不等于 degree[sibling[next x]]

并且 key[x] > key[next x]，则从根节点删除 x 并将其附加到 [next x]。

现在，让我们借助一个例子来理解两个二项堆的合并或联合。考虑两个二项堆：

我们可以看到有两个二项堆，所以，首先，我们必须组合这两个堆。要组合堆，我们首先需要按递增顺序排列它们的二项树。

在上面的堆中，首先，指针 x 指向度为 B₀ 的节点 12，指针 next[x] 指向度为 B₀ 的节点 18。度为 B₁ 的节点 7 是 18 的兄弟节点，因此，它表示为 sibling[next[x]]。

现在，首先应用情况 1，它说 **“如果 degree[x] ≠ degree[next x]，则将指针向前移动”**，但在上面的例子中，degree[x] = degree[next[x]]，所以这种情况不适用。

现在，应用情况 2，它说 **“如果 degree[x] = degree[next x] = degree[sibling(next x)]，则将指针向前移动”**。所以，这种情况也不适用于上面的堆。

现在，应用情况 3，它说 **“如果 degree[x] = degree[next x] ≠ degree[sibling[next x]] 并且 key[x] < key[next x]，则从根节点删除 [next x] 并将其附加到 x”**。我们将应用此情况，因为上面的堆遵循情况 3 的条件：

degree[x] = degree[next x] ≠ degree[sibling[next x]] {即，B₀ = B₀¬ ≠ B₁} 并且 key[x] < key[next x] {即 12 < 18}。

所以，删除节点 18 并将其附加到 12，如下图所示：

x = 12, next[x] = 7, sibling[next[x]] = 3, 并且 degree[x] = B₁, degree[next[x]] = B₁, degree[sibling[next[x]]] = B₁

现在，我们将重新应用上述二项堆中的情况。首先，我们将应用情况 1。由于 x 指向节点 12，next[x] 指向节点 7，x 的度等于 next x 的度；因此，情况 1 不适用。

这里，情况 2 是有效的，因为 x、next[x] 和 sibling[next[x]] 的度相等。因此，根据情况，我们将指针向前移动。

因此，**x = 7, next[x] = 3, sibling[next[x]] = 15,** 并且 **degree[x] = B₁, degree[next[x]] = B₁, degree[sibling[next[x]]] = B₂**

现在，让我们尝试应用情况 3，这里，情况 3 的第一个条件已满足，因为 degree[x] = degree[next[x]] ≠ degree[sibling[next[x]]]，但情况 3 的第二个条件 (key[x] < key[next x]) 不满足。

现在，让我们尝试应用情况 4。因此，情况 4 的第一个条件已满足，第二个条件 (key[x] > key[next x]) 也已满足。因此，从根节点删除 x 并将其附加到 [next[x]]。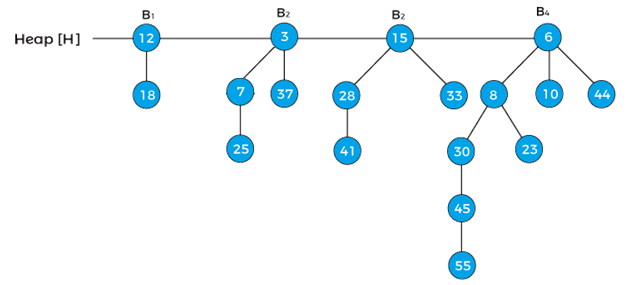

现在，指针 x 指向节点 3，next[x] 指向节点 15，sibling[next[x]] 指向节点 6。由于 x 的度等于 next[x] 的度，但不等于 degree[sibling[next[x]]]，并且 x 的键值小于 next[x] 的键值，因此，我们需要删除 next[x] 并将其附加到 x，如下图所示：

现在，x 指向节点 3，next[x] 指向节点 6。由于 x 和 next[x] 的度不相等，因此情况 1 是有效的。因此，将指针向前移动。现在，指针 x 指向节点 6。

B4 是堆中最后一个二项树，因此导致循环终止。上面的树是合并两个二项堆后的最终树。

在堆中插入元素

在堆中插入元素可以通过仅创建包含要插入的元素的堆，然后将其与原始堆合并来完成。由于合并，堆中的单次插入需要 O(logn) 时间。现在，让我们通过一个例子来理解在堆中插入新节点的过程。

在上面的堆中，有三棵度为 0、1 和 2 的二项树，其中 B0 附加在堆的头部。

假设我们必须在上面的堆中插入节点 15。

首先，我们必须组合这两个堆。由于节点 12 和节点 15 的度都为 0，因此节点 15 被附加到节点 12，如下图所示：

现在，将 x 分配给值为 12 的 B₀，将 next(x) 分配给值为 15 的 B₀，并将 sibling(next(x)) 分配给值为 7 的 B₁。由于 x 和 next(x) 的度相等。x 的键值小于 next(x) 的键值，因此 next(x) 被移除并附加到 x。如下图所示：

现在，x 指向度为 B₁ 的节点 12，next(x) 指向度为 B₁ 的节点 7，sibling(next(x)) 指向度为 B₂ 的节点 15。x 的度等于 next(x) 的度，但不等于 sibling(next(x)) 的度。x 的键值大于 next(x) 的键值；因此，x 被移除并附加到 next(x)，如下图所示：

现在，x 指向节点 7，next(x) 指向节点 15。x 和 next(x) 的度都为 B₂，并且 x 的键值小于 next(x) 的键值，因此 next(x) 将被移除并附加到 x，如下图所示：

现在，上述堆的度为 B₃，这是插入节点 15 后的最终二项堆。

提取最小键

这意味着我们需要删除具有最小键值的元素。我们知道，在最小堆中，根元素包含最小键值。因此，我们需要比较所有二项树根节点的键值。让我们来看一个从堆中提取最小键的例子。

假设堆是：

现在，比较上面堆中二项树根节点的键值。因此，上面堆中根节点的键值是 12、7 和 15，其中 7 是最小的；因此，从树中删除节点 7，如下图所示：

现在，节点 12 和节点 25 的度为 B₀，节点 15 的度为 B₂。指针 x 指向节点 12，next(x) 指向节点 25，sibling(next(x)) 指向节点 15。由于 x 的度等于 next(x) 的度，但不等于 sibling(next(x)) 的度。指针 x 的值小于指针 next(x)，因此节点 25 将被删除并附加到节点 12，如下图所示：