计数排序和桶排序的区别

计数排序算法

计数排序是一种处理输入值范围的排序算法。计数排序算法是一种整数排序算法。计数排序在某种程度上与其他排序方法不同，它是一种线性排序算法。

它计算每个元素的出现次数并直接确定它们的位置。这意味着它的运行时间为 O(N)，而最佳的基于比较的排序算法的复杂度为 O(N log N)（其中 N 是数组中的元素数量）。

基本概念

• 排序根据键进行。
• 计算具有不同键值的元素。

示例

让我们考虑一个长度为 N 的数组 A，我们将使用计数排序对其进行排序，以及一个长度为 K 的计数数组，其中 K = max_ele - min_ele + 1。

数组 A = {2,1,1,0,2,5,4,0,2,8,7,7,9,2,0,1,9}

伪代码

• 使用一个计数数组来存储输入数组 A 中所有唯一数字的计数。
• 修改计数数组，使每个索引处的元素存储过去计数的总和。
• 现在迭代 A，并将每个数字输出到其在输出数组中相关联的位置。

迭代步骤

说明

为了算法执行，我们使用一个辅助数组来存储数组中介于 0 到 N - 1 之间的每个元素的出现次数，然后使用该数组通过数学运算生成数组的排序版本。

这里我们使用一个额外的数组，这会增加空间复杂度。这使得它比其他算法稍贵，因为它只适用于范围，因此只适用于元素值范围接近数组大小且范围 = max_element - min_element + 1 的情况。

代码实现（Java）

下面列出的代码执行并计算负数。在这里，我们根据最小元素和存储在 0 处的计数进行计数。

空间复杂度：O(N)

修改计数数组：O(K)

将整数输出到输出数组：在最坏情况下，O(N)。

总时间复杂度：O(kn)

实际上，它变为 O(N)。

桶排序算法

桶排序是一种主要用于数据在一定范围内均匀分布的起始算法。顾名思义，在桶排序中，我们有几个称为桶的组，每个桶包含输入数组的指定元素。然后，每个桶通过递归应用相同的桶算法或适当的排序算法进行排序。

桶排序的基本步骤

• 将范围划分为固定数量的组。
• 将元素放入适当的组后，迭代这些元素。
• 使用某种排序算法单独对桶进行排序。
• 然后，将这些组链接在一起。

方法

让我们考虑一个例子。

A = {10, 8, 20, 7, 16, 18, 12, 1, 23, 11}，其中 N = 元素数量 = 9

从给定数组中我们可以观察到元素在范围 [0,25) 内。我们可以使用的桶可以是以下范围：

桶 1 - [0-5]

桶 2 - [5-10]

桶 3 - [10-15]

桶 4 - [15-20]

桶 5 - [20-25]

我们可以看到五个具有分布范围的桶。

现在，元素根据其元素范围被推入桶中。

桶 1 - [1]

桶 2 - [7,8]

桶 3 - [10,11,12]

桶 4 - [16,18,20]

桶 5 - [23]

作为最后一步，我们只需将这些桶连接起来即可获得所需的输出数组。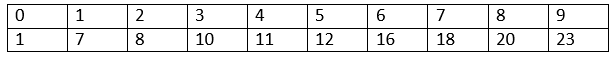

代码实现：Java

桶排序复杂度

复杂度的最佳情况 - 是数组已经排序且元素均匀划分，导致所有桶均匀分布的情况。如果我们也对桶中的元素进行排序，情况会更好。由于单个桶未排序，我们可以进一步使用插入排序来优化我们的复杂度。这将使我们的总体复杂度呈线性，即 O(N + k)，其中第一项用于桶之间的分布，而第二项表示通过在每个二叉堆或桶中使用插入排序将输入插入到桶中的正确位置。在最佳情况下，桶排序的时间复杂度为 O(N + k)。

平均情况复杂度 - 发生在没有适当升序或降序排序的情况下。即使元素均匀分布，桶排序仍然是线性时间。平均情况时间复杂度的复杂度阶数为 N + K。

最坏情况复杂度 - 发生在元素彼此接近时。它表示微小的偏差，由于此属性，它们被放入同一个桶中，其中一些桶包含的项比其他桶多。如果涉及反向列出的元素，情况将进一步发展，尽管它已经足够复杂。桶排序的时间复杂度为 O(n2)。

计数排序与桶排序

结论

总而言之，计数排序和桶排序都是线性排序算法，它们利用输入数据的一些特性来获得效率。计数排序的时间复杂度为 O (KN)，其中 K 是输入值的范围，对于相对于 N 较小的范围非常有效。尽管其计数数组导致空间复杂度为 O(N)，但另一个方面使计数排序在用于小值时稳定且最优。

然而，桶排序旨在将元素分布到桶中并独立地对它们进行排序，而不是在每个桶内使用另一种算法（如插入排序）。它适用于均匀分布的数据，平均时间复杂度为 O(n + k)，但最坏情况发生在元素分组时，相应的时​​间复杂度为 O(n^2)。桶排序在减少比较和加快处理方面具有优势，即使对于均匀分布的元素也是如此，但如果数据集更大，效率可能会下降。