Comb Sort 算法

在本文中，我们将讨论 Comb Sort 算法。Comb Sort 是冒泡排序的改进版本。冒泡排序会比较所有相邻的元素，而 Comb Sort 则会消除列表末尾的“乌龟”值或小值。

它是一种基于比较的排序算法，主要是对冒泡排序的改进。在冒泡排序中，通过比较相邻元素来对给定数组进行排序。因此，在冒泡排序中，被比较元素之间的间隔为 1。Comb Sort 通过使用大于 1 的间隔来改进冒泡排序。Comb Sort 中的间隔从一个较大的值开始，然后以 1.3 的因子缩小。这意味着在每个阶段完成后，间隔都会除以缩小因子 1.3。迭代将继续，直到间隔为 1。

通过对 200,000 个随机列表进行测试，发现缩小因子为 1.3。Comb Sort 的效果优于冒泡排序，但其平均情况和最坏情况的时间复杂度仍为 O(n²)。

执行 Comb Sort 的过程如下：

步骤 1 开始

步骤 2 计算间隔值，如果间隔值 == 1，则转到步骤 5，否则转到步骤 3

步骤 3 遍历数据集，并将每个元素与间隔元素进行比较，然后转到步骤 4。

步骤 4 如果需要，交换元素，否则转到步骤 2

步骤 5 打印排序后的数组。

步骤 6 停止

现在，让我们看看 Comb Sort 算法。

算法

Comb Sort 算法的工作原理

现在，让我们看看 Comb Sort 算法的工作原理。

为了理解 Comb Sort 算法的工作原理，让我们取一个未排序的数组。通过示例更容易理解 Comb Sort。

设数组的元素为：

现在，初始化

n = 8 // 数组大小

gap = n

shrink = 1.3

swapped = true

第一次迭代

gap = floor(gap/shrink) = floor(8/1.3) = 6

swapped = false

此迭代在此处结束，因为在 i = 2 时，i + gap = 2 + 6 = 8，数组的第 8 个位置没有元素。因此，在第一次迭代后，数组的元素将是：

现在，进入第二次迭代。

第二次迭代

gap = floor(gap/shrink) = floor(6/1.3) = 4

swapped = false

此迭代在此处结束，因为在 i = 4 时，i + gap = 4 + 4 = 8，数组的第 8 个位置没有元素。因此，在第二次迭代后，数组的元素将是：

现在，进入第三次迭代。

第三次迭代

gap = floor(gap/shrink) = floor(4/1.3) = 3

swapped = false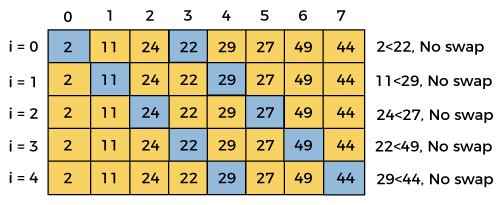

此迭代在此处结束，因为在 i = 5 时，i + gap = 5 + 3 = 8，数组的第 8 个位置没有元素。因此，在第三次迭代后，数组的元素将是：

现在，进入第四次迭代。

第四次迭代

gap = floor(gap/shrink) = floor(3/1.3) = 2

swapped = false

此迭代在此处结束，因为在 i = 6 时，i + gap = 6 + 2 = 8，数组的第 8 个位置没有元素。因此，在第四次迭代后，数组的元素将是：

现在，进入第五次迭代。

第五次迭代

gap = floor(gap/shrink) = floor(2/1.3) = 1

swapped = false

第五次迭代后，排序后的数组是：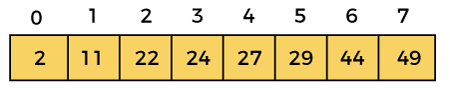

因此，迭代在此处结束，排序完成。现在，最终排序后的数组是：

Comb sort 复杂度

现在，让我们看看 Comb Sort 在最佳情况、平均情况和最坏情况下的时间复杂度。我们还将了解 Comb Sort 的空间复杂度。

1. 时间复杂度

• 最佳情况复杂度 - 当不需要排序时，即数组已排序时，会出现这种情况。Comb Sort 的最佳情况时间复杂度为 θ(n log n)。
• 平均情况复杂度 - 当数组元素处于混乱顺序时，即既不是完全升序也不是完全降序时，会出现这种情况。Comb Sort 的平均情况时间复杂度为 Ω(n²/2^p)，其中 p 是增量数。。
• 最坏情况复杂度 - 当数组元素需要反向排序时，会出现这种情况。也就是说，假设您需要按升序对数组元素进行排序，但其元素是降序的。Comb Sort 的最坏情况时间复杂度为 O(n²)。

2. 空间复杂度

• Comb Sort 的空间复杂度为 O(1)。

Comb Sort 的实现

现在，让我们看看不同编程语言中 Comb Sort 的程序。

程序：编写一个 C 语言实现 Comb Sort 的程序。

输出

说明

在上面的代码中，我们创建了一个 combSort()。此方法接受两个参数。此方法根据上述算法帮助对数组进行排序。我们还创建了一个 update()。此方法帮助我们计算数组中的间隔数。此代码是用 C 语言编写的。

程序：编写一个 C++ 实现 Comb Sort 的程序。

输出

说明

在上面的代码中，我们创建了一个 combSort()。此方法接受两个参数。此方法根据上述算法帮助对数组进行排序。我们还创建了一个 update()。此方法帮助我们计算数组中的间隔数。此代码是用 C++ 语言编写的。

程序：编写一个 C# 实现 Comb Sort 的程序。

输出

说明

在上面的代码中，我们创建了一个 combSort()。此方法接受两个参数。此方法根据上述算法帮助对数组进行排序。我们还创建了一个 update()。此方法帮助我们计算数组中的间隔数。此代码是用 C# 语言编写的。

程序：编写一个 Java 实现 Comb Sort 的程序。

输出

说明

在上面的代码中，我们创建了一个 combSort()。此方法接受两个参数。此方法根据上述算法帮助对数组进行排序。我们还创建了一个 update()。此方法帮助我们计算数组中的间隔数。此代码是用 Java 语言编写的。

程序：编写一个 PHP 实现 Comb Sort 的程序。

输出

说明

在上面的代码中，我们创建了一个 combSort()。此方法接受两个参数。此方法根据上述算法帮助对数组进行排序。我们还创建了一个 update()。此方法帮助我们计算数组中的间隔数。此代码是用 PHP 语言编写的。

Comb Sort 的特点

1. 它是一种基于比较的排序技术。
2. 它也是一种原地排序技术，因为不需要额外的存储空间。
3. 它也类似于冒泡排序，但比冒泡排序更有效。
4. 在这种技术中，通过在特定间隔处交换元素（如果它们未处于正确顺序）来进行排序。

Comb Sort 的优点

使用 Comb Sort 有一些优点。这些如下：

1. 在元素排序过程中不需要额外的空间。
2. 冒泡排序和 Comb Sort 类似，但 Comb Sort 比冒泡排序更有效。
3. Comb Sort 的逻辑非常简单易懂。
4. Comb Sort 的性质非常可靠。
5. 此排序技术非常适合小型数据库。

Comb Sort 的缺点

使用 Comb Sort 也有一些缺点。这些如下：

1. Comb Sort 的最坏情况复杂度与冒泡排序的最坏情况复杂度相似。
2. 它对于大量数据库效率不高。
3. 它不是稳定的排序。

所以，这就是关于本文的全部内容。希望本文能对您有所帮助并提供信息。

本文不仅限于算法。除了算法，我们还讨论了 Comb Sort 的复杂性、工作原理以及在不同编程语言中的实现。