数据结构中树的应用

2025年3月17日 | 阅读13分钟

引言

树是一种基本的数据结构，在计算机科学和编程中起着至关重要的作用。它提供了一种有效的方法来存储和组织数据，从而在不同领域实现各种应用。

树的概述

在深入探讨应用之前，让我们简要回顾一下树的概念。树是一种分层数据结构，由通过边连接的节点组成。它以一个根节点开始，分叉成子节点，形成类似树的结构。每个节点可以有零个或多个子节点，节点之间的连接通常表示为有向边。

树可以分为各种类型，例如二叉树、二叉搜索树、AVL 树、B 树等。每种类型都有其特定的属性和应用，但它们都共享树结构的基本特征。

应用

树在各种领域都有应用，包括文件系统、数据库、网络路由等。下面列出了树在二叉搜索树、表达式树、决策树、Trie 树和 AVL 树方面的不同应用。

二叉搜索树

二叉搜索树 (BST) 是一种重要的树形数据结构，在各种应用中得到广泛使用。BST 具有有序的属性，其中每个节点的值都大于其左子树中的所有值，而小于其右子树中的所有值。

应用

有序属性使得 BST 在搜索、插入和删除操作方面效率很高。

它们经常用于数据库系统，以及实现动态集合和字典。

二叉搜索树通过根据目标值进行比较来遍历树，从而实现快速搜索，允许对数时间复杂度。

为了说明树的应用，让我们看一个在 C++ 中实现二叉搜索树的例子。

#include <iostream>
using namespace std;

// Binary Search Tree Node Definition
struct BSTNode {
    int data;
    BSTNode* left;
    BSTNode* right;
};

// Function to create a new BST node
BSTNode* createNode(int data) {
    BSTNode* newNode = new BSTNode;
    newNode->data = data;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to insert a value into a BST
BSTNode* insertNode(BSTNode* root, int data) {
    if (root == nullptr) {
        return createNode(data);
    }

    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }

    return root;
}

// Function to perform in-order traversal of the BST (display elements in ascending order)
void displayInOrder(BSTNode* root) {
    if (root == nullptr) {
        return;
    }

    displayInOrder(root->left);
    cout << root->data << " ";
    displayInOrder(root->right);
}

// Sample usage
int main() {
    BSTNode* root = nullptr;

    root = insertNode(root, 50);
    root = insertNode(root, 30);
    root = insertNode(root, 20);
    root = insertNode(root, 40);
    root = insertNode(root, 70);
    root = insertNode(root, 60);
    root = insertNode(root, 80);

    cout << "Elements in the BST (in-order traversal): ";
    displayInOrder(root);
    cout << endl;

    return 0;
}

说明

程序通过定义一个名为 BSTNode 的结构体开始，它代表二叉搜索树中的一个节点。每个节点包含一个整数 data 来存储值，以及指向其左子节点和右子节点的指针 left 和 right。
createNode 函数用于创建新的 BST 节点并初始化其值和子节点。它以整数 data 作为输入，并返回指向新创建节点的指针。
insertNode 函数将具有给定值的新节点插入二叉搜索树。它递归地遍历树以找到合适的插入位置。
如果值小于当前节点的值，则移动到左子节点；如果值更大，则移动到右子节点。一旦找到合适的位置，就会创建一个新节点并将其指定为当前节点的子节点。
displayInOrder 函数对二叉搜索树执行中序遍历。它递归地访问左子树，打印当前节点的值，然后递归地访问右子树。这将导致元素按升序显示。
在 main 函数中，通过插入值分别为 50、30、20、40、70、60 和 80 的节点来创建二叉搜索树。

程序输出

表达式树

表达式树用于以树状结构表示数学表达式。树中的每个节点代表一个运算符或操作数，叶节点是操作数。

应用

表达式树有利于高效地评估和操作数学表达式。

它们在编译器、计算器和符号数学中都有应用。

表达式树在符号计算系统中用于符号地操作数学表达式，而不是进行数值评估。

为了说明树的应用，让我们看一个在 C++ 中实现表达式树的例子。

#include <iostream>
using namespace std;


// Expression Tree Node Definition
struct ExpTreeNode {
    string value;
    ExpTreeNode* left;
    ExpTreeNode* right;
};

// Function to create a new expression tree node
ExpTreeNode* createNode(string value) {
    ExpTreeNode* newNode = new ExpTreeNode;
    newNode->value = value;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to perform a preorder traversal and print the expression tree
void printExpressionTree(ExpTreeNode* node) {
    if (node == nullptr)
        return;

    cout << node->value << " ";
    printExpressionTree(node->left);
    printExpressionTree(node->right);
}

int main() {
    ExpTreeNode* root = createNode("+");
    ExpTreeNode* child1 = createNode("3");
    ExpTreeNode* child2 = createNode("*");
    ExpTreeNode* grandchild1 = createNode("5");
    ExpTreeNode* grandchild2 = createNode("2");

    root->left = child1;
    root->right = child2;
    child2->left = grandchild1;
    child2->right = grandchild2;

    cout << "Expression Tree: ";
    printExpressionTree(root);
    cout << endl;

    return 0;
}

说明

程序通过定义一个名为 ExpTreeNode 的结构体开始，它代表表达式树中的一个节点。
每个节点包含一个字符串 value 来存储运算符或操作数，以及两个指针 left 和 right 指向其左子节点和右子节点。
createNode 函数用于创建新节点并初始化其值和子节点。它接受一个字符串参数 value 并返回指向新创建节点的指针。
printExpressionTree 函数对表达式树执行前序遍历并打印每个节点的值。
前序遍历首先访问根节点，然后是左子树，最后是右子树。在此函数中，打印当前节点的值，然后递归调用打印左子树，然后是右子树。
在 main 函数中，通过创建节点并使用指针将它们链接在一起，构建了一个表达式树。
根节点以“+”的值创建，并为操作数和运算符创建了其他节点。然后通过分配适当的指针来连接节点。
最后，调用带有根节点的 printExpressionTree 函数以前序遍历的形式打印表达式树。

程序输出

决策树

决策树是数据结构中树的另一个流行应用，尤其是在机器学习和人工智能领域。

在决策树中，每个内部节点代表基于特定特征的决策，每个叶节点代表一个类标签或数值。通过从根节点到叶节点的决策树进行遍历，我们可以根据特征值进行预测或决策。

应用

决策树提供了可解释性，并广泛用于预测建模、数据挖掘和模式识别等领域。

它们在处理分类和数值数据方面都很有效，使其成为解决各种现实问题的高度通用的工具。

决策树通过根据特征值递归地划分数据来用于分类和回归任务。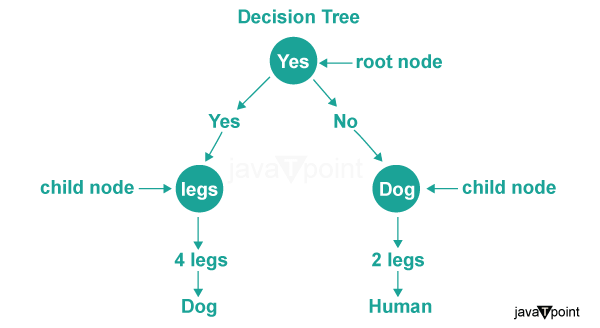

为了说明树的应用，让我们看一个在 C++ 中实现决策树的例子。

#include<iostream> 
using namespace std;

// Decision Tree Node Definition
struct DecisionTreeNode {
    string feature;
    DecisionTreeNode* left;
    DecisionTreeNode* right;
};

// Function to create a new decision tree node
DecisionTreeNode* createNode(string feature) {
    DecisionTreeNode* newNode = new DecisionTreeNode;
    newNode->feature = feature;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to make a decision based on given feature values
string makeDecision(DecisionTreeNode* node, string fur, string legs) {
    if (node == nullptr) {
        return ""; // Invalid decision
    }

    if (node->feature == "fur") {
        if (fur == "yes") {
            return makeDecision(node->left, fur, legs); // Traverse left
        } else if (fur == "no") {
            return makeDecision(node->right, fur, legs); // Traverse right
        }
    } else if (node->feature == "legs") {
        if (legs == "4") {
            return "Dog";
        } else if (legs == "2") {
            return "Human";
        }
    }

    return ""; // Invalid decision
}

// Sample usage
int main() {
    DecisionTreeNode* root = createNode("fur");
    DecisionTreeNode* furYes = createNode("legs");
    DecisionTreeNode* furNo = createNode("legs");

    root->left = furYes;
    root->right = furNo;

    furYes->left = createNode("");
    furYes->right = createNode("");
    furNo->left = createNode("");
    furNo->right = createNode("");

    string fur, legs;
    cout << "Does the animal have fur? (yes/no): ";
    cin >> fur;
    cout << "How many legs does the animal have? (2/4): ";
    cin >> legs;

    string decision = makeDecision(root, fur, legs);
    if (decision == "") {
        cout << "Invalid decision." << endl;
    } else {
        cout << "The animal is a " << decision << "." << endl;
    }

    return 0;
}

说明

程序通过定义一个名为 DecisionTreeNode 的结构体开始，它代表决策树中的一个节点。
每个节点包含一个字符串 feature 来存储用于做出决策的特征，以及两个指针 left 和 right 指向其左子节点和右子节点。
createNode 函数用于创建新节点并初始化其特征和子节点。它接受一个字符串参数 feature 并返回指向新创建节点的指针。
makeDecision 函数用于遍历决策树并根据给定的特征值做出决策。
它接受一个节点指针和两个字符串，分别代表“毛皮”和“腿”特征的值。
该函数根据特征值递归地遍历树，直到到达叶节点，然后返回分类决策。
在 main 函数中，通过创建节点并使用指针将它们链接在一起，构建了一个决策树。
用户被提示输入动物的“毛皮”和“腿”特征的值。使用根节点和输入的特征值调用 makeDecision 函数来确定分类决策。

程序输出

Trie 树

Trie 树，也称为前缀树，用于高效地存储和搜索字符串。Trie 中的每个节点代表一个字符，边代表下一个可能的字符。通过遍历树，可以快速搜索单词或单词的前缀。

应用

它们对于自动完成、拼写检查和字典实现等应用程序特别有用。

Tries 树用于网络和路由协议进行 IP 地址查找。

Tries 树在文本处理任务中有应用，例如搜索、索引和信息检索。

为了说明树的应用，让我们看一个在 C++ 中实现 Trie 树的例子。

#include <iostream>
#include <unordered_map>
#include <vector>

using namespace std;

// Trie Node Definition
struct TrieNode {
    bool isEndOfWord;
    unordered_map<char, TrieNode*> children;
};

// Function to create a new Trie node
TrieNode* createNode() {
    TrieNode* newNode = new TrieNode;
    newNode->isEndOfWord = false;
    return newNode;
}

// Function to insert a word into the Trie
void insertWord(TrieNode* root, string word) {
    TrieNode* curr = root;

    for (char c : word) {
        if (curr->children.find(c) == curr->children.end()) {
            curr->children[c] = createNode();
        }
        curr = curr->children[c];
    }
    curr->isEndOfWord = true;
}

// Function to output all the words in the Trie
void outputWords(TrieNode* root, string prefix = "") {
    if (root == nullptr) {
        return;
    }

    if (root->isEndOfWord) {
        cout << prefix << endl;
    }

    for (const auto& pair : root->children) {
        char c = pair.first;
        TrieNode* child = pair.second;
        outputWords(child, prefix + c);
    }
}

// Sample usage
int main() {
    TrieNode* root = createNode();

    insertWord(root, "apple");
    insertWord(root, "banana");
    insertWord(root, "orange");
    insertWord(root, "pear");

    cout << "Words in the Trie:" << endl;
    outputWords(root);

    return 0;
}

说明

程序通过定义一个名为 TrieNode 的结构体开始，它代表 Trie 中的一个节点。
每个节点包含一个布尔标志 isEndOfWord 来指示它是否代表单词的结尾，以及一个无序映射 of children 来存储对应于不同字符的子节点。
createNode 函数用于创建新的 Trie 节点并将其 isEndOfWord 标志初始化为 false。
insertWord 函数用于将单词插入 Trie。它以 TrieNode 指针 root 和字符串 word 作为输入。
该函数遍历单词中的每个字符，检查该字符是否存在为当前节点的子节点。如果不存在，则创建一个新节点并将其添加为子节点。
然后，该函数将当前节点移动到对应于当前字符的子节点。最后，将代表单词结尾的最后一个节点的 isEndOfWord 标志设置为 true。
outputWords 函数是一个递归函数，用于输出 Trie 中存储的所有单词。
它接受 TrieNode 指针 root 和字符串 prefix（可选）作为输入。该函数递归地遍历 Trie，在遇到 isEndOfWord 为 true 的节点时打印单词。
它还将每个节点的字符附加到前缀字符串以形成完整的单词。
在 main 函数中，通过使用 createNode 创建根节点来创建 Trie。使用 insertWord 函数将“apple”、“banana”、“orange”和“pear”等单词插入 Trie。

程序输出

AVL 树

AVL 树是自平衡二叉搜索树，通过确保任何节点的左右子树的高度之差最多为 1 来保持平衡。它们确保树保持平衡，从而实现 O(log n) 时间复杂度的有效操作。

应用

AVL 树在保持平衡至关重要的场景中有应用，例如数据库系统、索引和动态集合。

通过执行旋转和重新平衡操作，AVL 树即使在动态插入和删除时也能保证最佳性能。

AVL 树在网络路由算法中有应用，特别是在维护路由表方面。

为了说明树的应用，让我们看一个在 C++ 中实现 AVL 树的例子。

#include <iostream>
using namespace std;

// AVL Tree Node Definition
struct AVLNode {
    int data;
    int height;
    AVLNode* left;
    AVLNode* right;
};

// Function to create a new AVL node
AVLNode* createNode(int data) {
    AVLNode* newNode = new AVLNode;
    newNode->data = data;
    newNode->height = 1;
    newNode->left = newNode->right = nullptr;
    return newNode;
}

// Function to calculate the height of a node
int getHeight(AVLNode* node) {
    if (node == nullptr) {
        return 0;
    }
    return node->height;
}

// Function to calculate the balance factor of a node
int getBalanceFactor(AVLNode* node) {
    if (node == nullptr) {
        return 0;
    }
    return getHeight(node->left) - getHeight(node->right);
}

// Function to perform left rotation
AVLNode* leftRotate(AVLNode* root) {
    AVLNode* newRoot = root->right;
    AVLNode* subtree = newRoot->left;

    newRoot->left = root;
    root->right = subtree;

    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;

    return newRoot;
}

// Function to perform right rotation
AVLNode* rightRotate(AVLNode* root) {
    AVLNode* newRoot = root->left;
    AVLNode* subtree = newRoot->right;

    newRoot->right = root;
    root->left = subtree;

    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    newRoot->height = max(getHeight(newRoot->left), getHeight(newRoot->right)) + 1;

    return newRoot;
}

// Function to insert a value into an AVL tree
AVLNode* insertNode(AVLNode* root, int data) {
    if (root == nullptr) {
        return createNode(data);
    }

    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    } else {
        return root; // Duplicate values not allowed
    }

    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;

    int balance = getBalanceFactor(root);

    // Perform necessary rotations to balance the tree
    if (balance > 1) {
        if (data < root->left->data) {
            return rightRotate(root);
        } else {
            root->left = leftRotate(root->left);
            return rightRotate(root);
        }
    } else if (balance < -1) {
        if (data > root->right->data) {
            return leftRotate(root);
        } else {
            root->right = rightRotate(root->right);
            return leftRotate(root);
        }
    }

    return root;
}

// Function to display the elements of the AVL tree (in-order traversal)
void displayInOrder(AVLNode* root) {
    if (root == nullptr) {
        return;
    }

    displayInOrder(root->left);
    cout << root->data << " ";
    displayInOrder(root->right);
}

// Sample usage
int main() {
    AVLNode* root = nullptr;

    root = insertNode(root, 10);
    root = insertNode(root, 20);
    root = insertNode(root, 30);
    root = insertNode(root, 40);
    root = insertNode(root, 50);
    root = insertNode(root, 25);

    cout << "Elements in the AVL tree (in-order traversal): ";
    displayInOrder(root);
    cout << endl;

    return 0;
}

说明

程序通过定义一个名为 AVLNode 的结构体开始，它代表 AVL 树中的一个节点。每个节点包含一个整数 data 来存储值，一个整数 height 来存储节点的高度，以及指向其左子节点和右子节点的指针 left 和 right。
createNode 函数用于创建新的 AVL 节点并初始化其值。它以整数 data 作为输入，并返回指向新创建节点的指针。
getHeight 函数计算节点的高度。如果节点是 nullptr，则返回 0；否则，返回节点中存储的高度值。
getBalanceFactor 函数计算节点的平衡因子。它从左子树的高度中减去右子树的高度。
leftRotate 函数对给定的根节点执行左旋转。它重新分配旋转中涉及的节点的指针并相应地更新它们的高度。
rightRotate 函数对给定的根节点执行右旋转。它重新分配旋转中涉及的节点的指针并相应地更新它们的高度。
insertNode 函数将具有给定值的新节点插入 AVL 树。它递归地遍历树以找到合适的插入位置。
插入后，它会更新当前节点的高度并检查平衡因子。如果平衡因子大于 1 或小于 -1，则执行必要的旋转来平衡树。
displayInOrder 函数对 AVL 树执行中序遍历，并按升序打印元素。
在 main 函数中，通过插入值分别为 10、20、30、40、50 和 25 的节点来创建 AVL 树。

程序输出

结论

总之，树是一种多功能且强大的数据结构，在各个领域都有应用。

树提供了一种表示分层关系（如文件系统、组织结构和 XML/HTML 解析）的有效方法。

二叉搜索树通过以分层顺序组织元素，从而实现数据的高效搜索，允许快速查找操作。

像 AVL 树和红黑树这样的树可以高效地对数据集执行排序和范围查询操作。

树可以用作实现各种图算法（如深度优先搜索 (DFS) 和广度优先搜索 (BFS)）的基础。

Trie 树对于高效的字符串匹配、自动完成功能和拼写检查应用程序很有用。

决策树为决策过程提供了一种结构化方法，其中节点代表决策，分支代表可能的输出。

树在数据结构中的应用非常广泛，并且随着新问题领域和挑战的出现而不断扩展。通过理解与树相关的特性和算法，开发人员可以利用它们的优势来高效有效地解决复杂问题。

下一个主题如何检查二进制数是否能被 3 整除

数据结构中树的应用

引言

树的概述

应用

二叉搜索树

应用

表达式树

决策树

Trie 树

AVL 树

结论

联系信息

关注我们

教程

面试题

在线编译器

Python

Java

.Net Framework

AI, ML and Data Science

Cloud Technology

B.Tech and MCA

Web Technology

PHP

Software Testing

Technical Interview

Java Interview

Python

Web Interview

Database Interview

B.Tech / MCA

Important Interview

Software Testing Interview

Company Interviews

Online Compilers

Multiple Choice Questions

数据结构教程

DS 数组

DS 链表

DS 栈

DS 队列

DS 树

DS 图

DS 搜索

DS 排序

哈希与堆

差异

二叉树

二叉搜索树

AVL 树

单向链表

双向链表

循环链表

循环双向链表

DS 选择题

其他

数据结构中树的应用

引言

树的概述

应用

二叉搜索树

应用

表达式树

决策树

Trie 树

AVL 树

结论

相关帖子

如何检查二进制数是否可被 3 整除

数据结构中的树顶点拆分

下一个回文数

实用拜占庭容错 (pBFT)

平衡二叉搜索树

二叉树的对角线遍历

排序算法的应用、优点和缺点

使用多项式滚动哈希函数进行字符串哈希

找出最后一个拿到票的人（队列中的问题）

检查给定数组是否包含相距 k 以内的重复元素

订阅 Tpoint Tech

联系信息

关注我们

教程

面试题

在线编译器