对称二叉树

在二叉树中，每个节点都有一个左子树和一个右子树。任何二叉树，包括空树、单节点树和子树，都可以存在。如果根节点的右子树和左子树互为镜像，则称该二叉树为对称的。

验证给定的二叉树是否与其自身镜像对称。

例如，下面的二叉树是对称的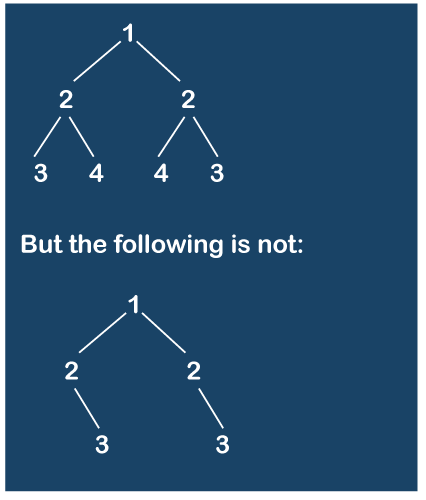

目标是创建一个名为 isMirror() 的递归方法，该方法接受两个树作为参数，如果两个树是镜像，则返回 true，否则返回 false。 isMirror() 方法通过递归地检查两个根节点及其下方的子树来工作。

方法

以下是算法步骤的简要概述

• 我们从两个变量 root1 和 root2 开始，它们都指向根节点。
• 然后使用任何树遍历方法遍历节点。在此遍历函数中，我们将同时修改 root1 和 root2。
• 在基本情况下，如果两者都指向 NULL，则返回 true，但如果仅一个指向 NULL 而另一个指向一个节点，则返回 false。
• 我们首先比较指向同一节点的任何两个节点的值，如果它们相等，则检查树的较低级别。
• 递归调用该函数，将 root1 的左子节点与 root2 的右子节点进行比较，然后再次将 root1 的右子节点与 root2 的左子节点进行比较。
• 如果所有三个条件——左节点和右节点的值以及两个递归调用——都得到满足，我们就从函数返回 true，否则返回 false。

上述算法的实现方式如下。

C 语言程序

输出

Symmetric

C++ 程序

输出

Symmetric

• 时间复杂度：O(N)
• 辅助空间：O(h)，其中 h 表示树的高度。