对给定矩阵进行排序

什么是矩阵？

1. 定义；矩阵是指组织成行和列的数字或元素的布局。它是一个二维数组，用于数据的表示和操作。
2. 符号；矩阵通常用大写字母（如 A、B、C）标识。矩阵内的特定元素用小写字母加上行和列的下标表示（例如 a₁₂ 表示矩阵 A 的第一行第二列的元素）。
3. 维度；矩阵的大小由其行数和列数决定。例如，一个包含 3 行 4 列的矩阵称为 3×4 矩阵。
4. 矩阵的类别；
   
   • 方阵： 此类矩阵的行数和列数相同（3×3、4×4）。
   • 长方阵： 相反，此类矩阵具有不同数量的行和列。
   • 对角矩阵： 主对角线（左上到右下）上只有非零元素的方阵。
   • 标量矩阵： 对角线元素都相等，非对角线元素都为零的方阵。
5. 运算；
   
   • 加法和减法： 您可以通过处理每个元素来对相同大小的矩阵进行加法或减法运算。
   • 标量乘法： 当您将矩阵乘以标量（常数）时，您基本上是将矩阵的每个元素乘以该常数。
   • 矩阵乘法： 如果第一个矩阵的列数与第二个矩阵的行数匹配，则可以对它们进行相乘。结果矩阵的维度将基于这些匹配的数字。
6. 应用；
   
   • 线性代数： 矩阵在代数中起着表示和求解线性方程组的作用。
   • 图形和计算机视觉： 在计算机图形学和图像处理中，矩阵对于通过旋转、缩放和平移等操作来变换图像至关重要。
   • 数据分析： 矩阵在数据分析任务中广泛用于组织和操作数据。
   • 机器学习： 矩阵及其运算是机器学习算法（如线性回归和神经网络）中的组成部分。
7. 性质
   
   • 转置： 要获得矩阵的转置，只需将其行与列交换即可。
   • 行列式是与矩阵相关的值，它有助于检查矩阵是否可逆以及求解线性方程组。
   • 矩阵的逆（如果存在）是另一个矩阵，当与原矩阵相乘时会产生单位矩阵。
   • 矩阵通过提供一种表示和处理多维数据的方法，在数学、计算机科学以及科学和工程的各个领域发挥着作用。

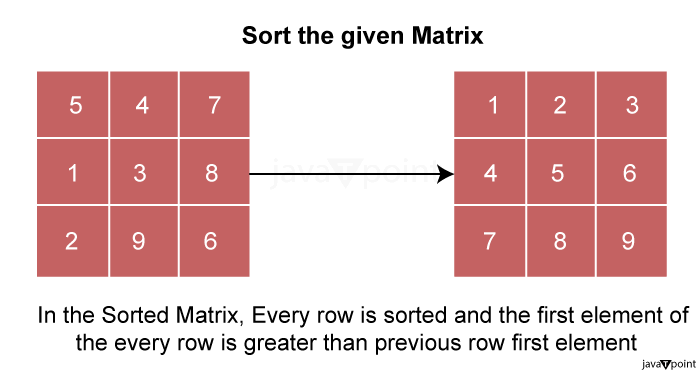方法 1：逐行或逐列排序

算法

逐行排序

1. 遍历矩阵的每一行。
2. 对于每一行，应用标准的排序算法，如冒泡排序、插入排序、选择排序、归并排序或快速排序来排序该行中的元素。
3. 对矩阵中的所有行重复步骤 2。

逐列排序

1. 通过交换行和列来创建原始矩阵的转置。
2. 遍历转置矩阵的每一行（这对应于原始列）。
3. 对于每一行，应用标准的排序算法，如冒泡排序、插入排序、选择排序、归并排序或快速排序来排序该行中的元素。
4. 对步骤 3 中的已排序矩阵进行转置，以获得逐列排序的原始矩阵。

Python 实现

输出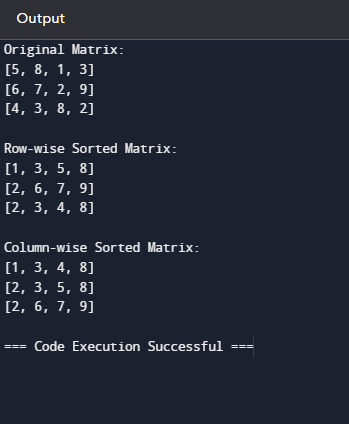

方法 2：展平并排序

算法

1. 将矩阵展平成一维（1D）数组，方法是逐行（或逐列）连接矩阵的所有元素。
2. 要对展平的 1D 数组进行排序，可以使用标准的排序算法，如冒泡排序、插入排序、选择排序、归并排序或快速排序。
3. 通过将排序后的 1D 数组分割回行（或列），根据原始矩阵的维度，从排序后的 1D 数组重构已排序的矩阵。

时间复杂度

展平并排序方法的 time complexity 取决于应用于 1D 数组的排序算法的类型。

• 当使用基于比较的排序方法（如快速排序或归并排序）时，time complexity 为 O(mn log mn)，其中 m 表示行数，n 表示矩阵的列数。这是因为展平的数组将包含 mn 个元素，而排序算法通常以 O(n log n) 的 time complexity 运行，其中 n 是数组的大小。
• 另一方面，使用计数排序或基数排序等非比较排序算法可以获得改进的 time complexity O(mn+k)，其中 k 表示矩阵中值的范围。尽管如此，这些算法也附带与输入数据相关的限制和要求。

Python 实现

输出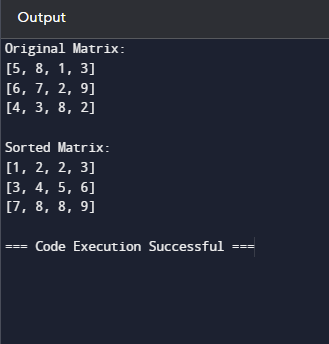

说明

1. 首先创建一个列表来存储展平的一维数组。
2. 遍历输入矩阵中的每一行。
3. 对于每一行，将其元素添加到前面创建的列表中。此步骤有助于将矩阵展平成一维数组。
4. 矩阵展平后，使用冒泡排序、插入排序、归并排序或快速排序等排序算法来排列一维数组中的元素。
5. 找出矩阵中有多少行和多少列。
6. 设置另一个列表来存储已排序的矩阵。
7. 从 0 开始迭代，直到行数减一。
8. 在每次迭代中，从一维数组中对应于当前行开始的位置切片一部分，直到匹配该行的结束位置。这个切片部分代表矩阵中的一行。
9. 将此行添加到步骤 6 中创建的列表中。
10. 遍历完所有行后，您将在步骤 6 中创建的列表中获得存储的矩阵。

将结果作为矩阵返回。

方法 3：桶排序或基数排序

桶排序

桶排序是一种排序算法，它将元素分配到若干个桶中，然后对每个桶进行排序，最后将排序后的桶连接起来得到最终的排序数组或矩阵。

对矩阵进行桶排序的算法如下：

1. 确定矩阵中值的范围（最小值和最大值）。
2. 创建一组空桶，为矩阵中每个可能的值或值的范围创建一个桶。
3. 遍历矩阵，并将每个元素根据其值放入相应的桶中。
4. 使用简单的排序算法（如插入排序）对每个桶中的元素进行排序。
5. 连接排序后的桶以得到最终排序的矩阵。

Python 实现

输出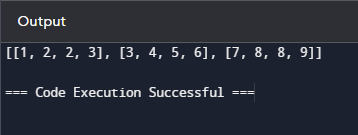

bucket_sort 函数首先查找矩阵中的值以确定值的范围。

然后它创建桶，每个桶代表该范围内的值。然后根据值将矩阵中的元素放入这些桶中。

随后，使用提供的排序方法对每个桶中的元素进行排序。最后，通过将每个桶中的元素添加回其行来重构已排序的矩阵。

基数排序

基数排序是一种排序技术，它通过从最高有效位到最低有效位检查数字来组织元素。

要将基数排序应用于矩阵，请执行以下步骤：

1. 识别矩阵中的一个元素以确定其数字位数。
2. 为每个数字值（数字为 0-9，以 10 为基数）创建桶（如队列或链表）。
3. 遍历矩阵。根据每个元素的最低有效数字将其分配到相应的桶中。
4. 分配完所有元素后，按升序（0-9）从桶中收集它们以重构矩阵。
5. 持续执行这些步骤，直到检查完所有数字。

Python 实现

输出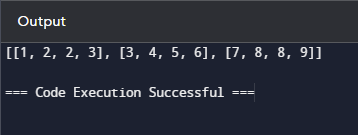

说明

1. radix_sort 函数查找矩阵中的最大元素以确定数字位数。
2. 它为每个位数（数字）调用 counting_sort 函数，从最低有效数字开始。
3. counting_sort 函数为数字（0-9）创建桶，并根据当前位数将元素分配到相应的桶中。
4. 从桶中连接元素以形成排序列表。
5. 将排序列表重新构建成行以形成已排序的矩阵。

桶排序和基数排序的 time complexity 分别取决于矩阵中值的范围和最大元素的数字位数。

• 对于桶排序，time complexity 为 O(n + k)，其中 n 是矩阵中的元素数量，k 是桶的数量。但是，这假定矩阵中值的分布是均匀的，并且每个桶内的排序需要常数时间。
• 对于基数排序，time complexity 为 O(d * (n + k))，其中 d 是任何元素中的最大数字位数，n 是矩阵中的元素数量，k 是桶的数量（十进制数为 10）。